Тема урока «Пересечение и объединение множеств». Дата урока ____________________
Тип урока: Урок «открытия» новых знаний.
Цель урока: ознакомить учащихся с возможностями иллюстрации соотношения между множествами с помощью кругов Эйлера; продолжить формировать умения находить объединение и пересечение множеств; закрепление умения определять принадлежность элементов множеству, подмножеству, пересечению или объединению множеств; задавать вопросы, наблюдать, анализировать, сравнивать; воспитание культуры общения со сверстниками и взрослыми.
Задачи:
Познавательные: формирование умений работать с математическим текстом, извлечение необходимой информации; овладение базовым понятийным аппаратом: развитие представлений о множествах и операций с ними; овладение символьным языком математики; формирование умений применять знания о числах, геометрических фигурах, знаний из других школьных дисциплин для решения задач исследовательского характера; формирование умений точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику.
Регулятивные: овладеть различными типами учебных действий, включая способность принимать и сохранять учебную цель и задачу, планировать ее реализацию, в том числе во внутреннем плане, контролировать и оценивать свои действия, вносить соответствующие коррективы в их выполнение.
Коммуникативные и личностные: формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками в исследовательской и творческой видах деятельности; развитие логического и критического мышления, культуры речи; развитие интереса к математическому творчеству и математических способностей. способствовать развитию способности к общению и сотрудничеству со сверстниками и взрослыми в процессе образовательной, общественно-полезной, учебно-исследовательской, творческой деятельности;
Оборудование и средства обучения: раздаточный материал (карточки), магниты, шаги алгоритма на отдельных листах (для доски), карточки для самостоятельной работы.
Формы организации труда: индивидуальная, фронтальная, работа в парах, самостоятельная.
Педагогические технологии: системно - деятельностный подход (технология проблемного обучения)
Методы обучения: словесный, наглядный, практический, репродуктивный, частично-поисковый.
Основные понятия: множества, объединение, пересечение, круги Эйлера.
Девиз урока: «Тот, кто хочет много знать, должен сам всё постигать»
ХАРАКТЕРИСТИКА УРОКА
Техноло-гии,
приме-няемые
на уроке
|
Решаемые
проблемы
|
Виды деятельности
(элементы содержания,
контроль)
|
Планируемые результаты
|
предметные
|
УУД
|
личностные
|
Проблем-ного обучения,
информационно- коммуни-кативные технологии, смыслового чтения
|
Выполнение операций над множествами.
|
устная работа, работа в паре, работа с текстом учебника, работа у доски, фронтальная работа с классом.
|
ПРЕДМЕТНЫЕ
Учащийся выполнять операции над множествами,
получит возможность научиться применять полученные знания в практической деятельности.
МЕТАПРЕДМЕТНЫЕ
ученик научится определять понятия, создавать обобщения, устанавливать аналогии с известными правилами;
ученик получит возможность научиться элементам волевой саморегуляции, мобилизации сил к преодолению препятствий.
|
Коммуникативные:
уметь точно и грамотно выражать свои мысли; уметь слушать и отвечать на вопросы других, умение находить общее решение, аргументировать свою точку зрения
Регулятивные: работать по составленному плану, формировать целевые установки учебной деятельности, выстраивать алгоритм действий; обнаруживают и формулируют учебную проблему совместно с учителем; умение адекватно оценивать правильность или ошибочность выполнения учебной задачи.
Познавательные: осуществлять поиск необходимой информации для выполнения учебных заданий,
умеют устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение;
|
Формирование познавательного интереса к изучению нового; проявление способности к эмоциональному восприятию математических объектов, задач, решений, рассуждений
ученик получит возможность контролировать процесс и результат учебной и математической деятельности
|
Структура урока
Этапы урока,
задачи этапа
|
Деятельность учителя
|
Деятельность учащихся
|
Формируемые УУД
|
1 этап.
Орг. момент. Самоопределение к деятельности.
- Создать благоприятный психологический настрой на работу
|
Здравствуйте, ребята!
Я рада приветствовать Вас на уроке математики.
Сегодня мы с вами отправимся в путь за новыми знаниями.
В дорогу мы возьмем только самое необходимое: хорошее настроение и наши прошлые наблюдения и знания.
|
Включаются в деловой ритм урока. В тетрадях записывают число и классная работа
Классная работа. 31.03.21 г
|
Личностные: эмоциональный настрой
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.
Регулятивные: организация своей учебной деятельности
|
2 этап.
Актуализация опорных знаний учащихся.
(3 мин.)
- Проверить изученный материал.
Стимулировать активность ученика на восприятие учебного материала.
|
Организует фронтальную работу с классом для актуализации имеющихся знаний и умений, демонстрирует задания с помощью доски.
Проверим домашнее задание
. № 804 (а).
Р е ш е н и е
– Вспомним определения.
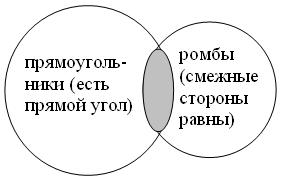
Прямоугольником называется параллелограмм, у которого есть прямой угол.
Ромбом называется параллелограмм, у которого смежные стороны равны.
Изобразим соотношение множества этих фигур с помощью кругов Эйлера.
Параллелограмм
|
Пересечением двух множеств будет множество параллелограммов, у которых есть прямой угол и равны смежные стороны. Это множество квадратов.
О т в е т: множество квадратов.
|
Отвечают на вопросы учителя. Все включаются в работу.
|
Познавательные: структурирование собственных знаний.
Коммуникативные:умение выражать свои мысли с достаточной точностью.
Регулятивные: контроль и оценка процесса и результатов деятельности.
|
3 этап. Целеполагание и мотивация. Создание проблемной ситуации.
-Обеспечение мотивации учения детьми. Подвести к формулированию цели урока, принятия ими целей урока
- Обеспечение восприятия, осмысления и первичного запоминания детьми изучаемой темы:
Пересечение и объединение множеств.
|
Устная работа. . Найдите А  В, если: В, если:
а) А = {0, 1, 2, 3, 4} и В = {1, 2, 3, 4, 5};
б) А = {х | х – двузначное число} и В = {х | х – число, меньше 75}.
3. Найдите А  В, если: В, если:
а) А = {17, 18, 19} и В = {3};
б) А = {у | у – число, меньшее 32} и В = {у | у – число, большее 7, но меньшее 45}.
|
Отвечают на вопросы.
Формулируют тему урока, цель.
Записывают тему в тетрадь
Пересечение и объединение множеств.
.
|
Коммуникативные: умение осознанно и произвольно строить речевое высказывание в устной форме; с достаточной полнотой и точностью выражают свои мысли;умение вступать в диалог, участвовать в коллективном обсуждении вопроса.
Регулятивные: целеполагание, умение самостоятельно определять цель своей учебной деятельности.
Личностные: мотивация учения; удовлетворяютпотребность в самовыражении
Познавательные:
структурировать знания, точно и грамотно выражать свои мысли с применением математической терминологии.
|
4 этап . Первичное восприятие и усвоение материала
Формирование умений читать вдумчиво, оценивать информацию, формулировать мысли. Уметь находить необходимую информации с новой задачей для её решения..
|
З а д а ч а. В классе 35 учеников. Из них 20 занимаются в математическом кружке, 11 – в биологическом, 10 ребят не посещают кружки. Сколько биологов увлекаются математикой?
Р е ш е н и е
Изобразим различные множества учащихся в виде кругов. Большой круг будет изображать всех учащихся класса. В этот круг поместим два поменьше. Один обозначим буквой М, и он будет изображать математиков класса. Другой круг обозначим Б – биологи класса. Очевидно, в общей части кругов, обозначенной МБ, окажутся те самые биологи-математики, которые нас интересуют. Теперь посчитаем: всего внутри большого круга 35 ребят, внутри двух меньших 35 – 10 = 25 ребят. Внутри «математического» круга М находятся 20 ребят, значит, в той части «биологического» круга, которая расположена вне круга М, находятся 25 – 20 = 5 биологов, не посещающих математический кружок. Остальные биологи, их 11 – 5 = 6 человек, находятся в общей части кругов МБ. Там образом, 6 биологов увлекаются математикой.
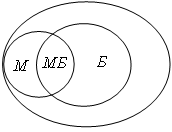
О т в е т: 6 биологов увлекаются математикой.
Решение задач с помощью кругов Эйлера. (См. приложение).
|
Выполняют работы в парах.
|
Регулятивные: Осуществлять взаимоконтроль, оценивать качество и уровень усвоения знаний
Коммуникативные: умение работать в парах, уважительно относиться к мнению других
Познавательные: построение логической цепи рассуждений.
Личностные: развитие навыков сотрудничества со взрослыми и сверстниками.
|
5 этап. Физкультминутка.
- Организовать смену деятельности, обеспечить эмоциональную разгрузку учащихся
|
Организует физкультминутку.
|
Выполняют физкультминутку
Учащиеся сменили вид деятельности и готовы продолжить работу.
|
|
6 этап. Закрепление теоретического материала при выполнении самостоятельной работы.
Формирование умений выполнять задание вдумчиво, оценивать информацию, формулировать мысли.
|
№ 806.
Р е ш е н и е
А = {х | х – кратное 4},
В = {у | у – кратное 3}.

А  В – множество чисел, которые одновременно делятся на 3 и на 4, значит, это множество чисел, кратных 12. В – множество чисел, которые одновременно делятся на 3 и на 4, значит, это множество чисел, кратных 12.
О т в е т: А  В = {z | z – кратное 12}. В = {z | z – кратное 12}.
|
Выполняют задания.
.
Учатся применять полученные знания в процессе групповой работы.
|
Регулятивные: оценивать качество и уровень усвоения знаний
Коммуникативные: умение работать в группах, уважительно относиться к мнению других
Познавательные: построение логической цепи рассуждений.
Личностные: развитие навыков сотрудничества со взрослыми и сверстниками.
|
7 этап.
Подведение итогов урока.
Дать качественную оценку работы класса и отдельных обучаемых
|
– Соответствовала ли наша работа целям урока?
- Что вызвало трудности?
- Были ли задания, которые ты делал с удовольствием?
- А как вы считаете, знания, полученные сегодня на уроке, будут вам необходимы на следующих уроках.
|
Подводят итог урока,
отвечают на вопросы, рассказывают, что узнали, смогли выполнить. Оценивают свою учебную деятельность
|
Коммуникативные: осознание себя в коллек-тиве, значимости совмест-ной работы, рефлексия своих действий, оцени-вание работы на уроке
Познавательные: выделение и осознание учащимися того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения
Регулятивные: оценка уровня и качества усвоения материала.
|
8 этап. Домашнее задание.
Обеспечение понимания детьми цели, содержания и способов выполнения домашнего задания
|
Озвучивает и записывает домашнее задание.
Выучить теоремы п. 32, решить № 807, № 808 (б).
|
Открывают дневники, записывают домашнее задание, задают вопросы.
|
Личностные: ответственное отношение к учению
|
9 этап. Рефлексия
Инициировать рефлексию детей по их собственной деятельности и взаимодействия с учителем и другими детьми в классе.
|
Оцените свою работу на уроке.
|
Оценивают себя
Учащиеся отвечают на вопросы.
Высказывают свои мнения.
|
Коммуникативные: осознание себя в коллективе, значимости совместной работы, рефлексия своих действий, оценивание работы на уроке
Личностные: самооценивание
|
Приложение 1.
В олимпиаде среди 8-х классов приняло участие 35 человек: по математике – 23 человека, 20 человек – по русскому языку и 24 человека – по истории. Олимпиаду и по математике и по русскому языку писали 9 человек, по математике и истории – 11 человек, русскому языку и истории – 10 человек. Сколько человек приняли участие во всех трех олимпиадах? Ответ: 1 человек.
Решение. 23 – (9+11+х) + 20 – (9+10+х) + 24 – (11+10+х) + 9 + 11+ 10 + х = 35
Х = 1
Все мои соседи выращивают цветы: только розы выращивают 16 человек, только лилии – 17 человек, только гладиолусы – 20 человек. Розы и гладиолусы есть у 11 человек, розы и лилии – у 9, лилии и гладиолусы – у 10 соседей. Все три вида цветов выращивают 8 соседей. Сколько у меня соседей? Ответ: 91 сосед
В доме детского творчества 20 ребят занимаются в театральной студии, 21 человек – в математическом кружке, 27 человек – в спортивной секции. 5 человек занимаются и в спортивной секции и в математическом кружке; 6 человек занимаются спортом и посещают театральную студию; 5 человек ходят в театральную студию и в математический кружок; 4 человека успевают посещать и театральную студию, и математический кружок, и заниматься спортом. Сколько всего детей занимается в доме детского творчества?
Решение. 20 + 21 + 27 – (5+6+5) -4*2 = 68-16-8 = 68 -24 = 44
Ответ: 44 ребенка. |
 Скачать 113 Kb.
Скачать 113 Kb.


