Задание 4: Применяя таблицы истинности, докажите тождественную истинность
логических формул:
1. 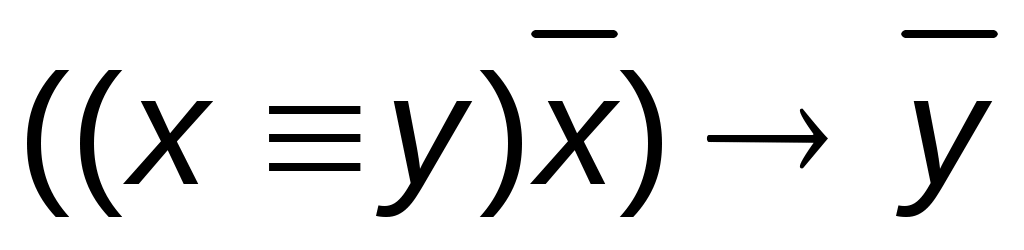 ; 2. ; 2. 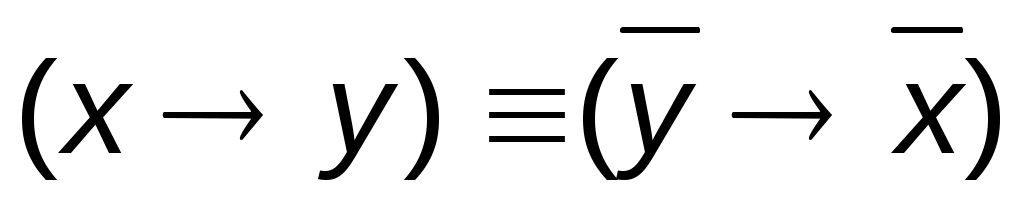 ; 3 ; 3 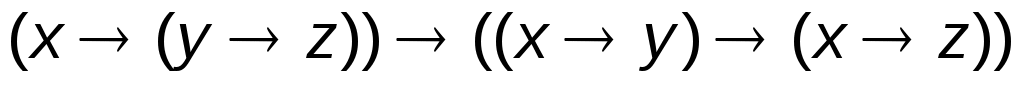 . .
1. 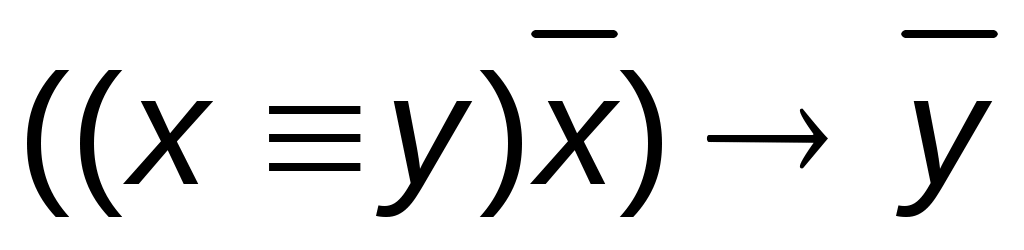 ; F1 ; F1
-
A
|
B
|
C
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
F
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
2. 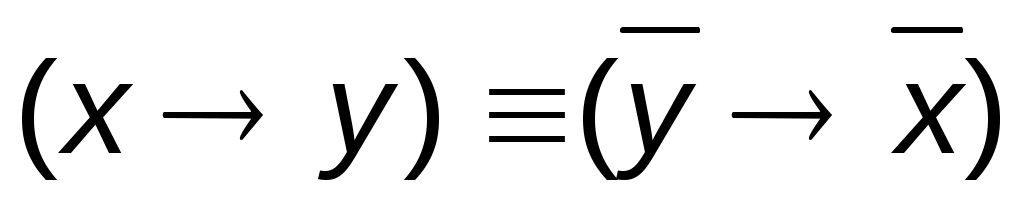 ; F2 ; F2
-
A
|
B
|
C
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
F
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
1
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
3 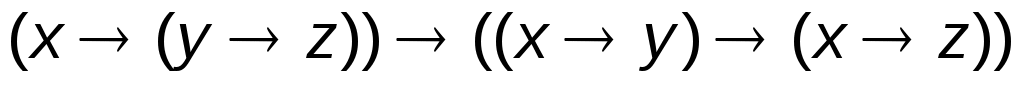 . F3 . F3
-
A
|
B
|
C
|
1
|
2
|
3
|
4
|
5
|
F
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
F1=F2=F3
Задание 5. Проверить, не составляя таблицы истинности, являются ли следующие
логические формулы тождественно ложными (противоречиями).
1. 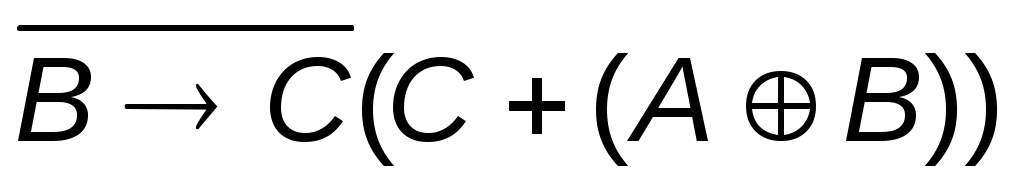 2. 2. 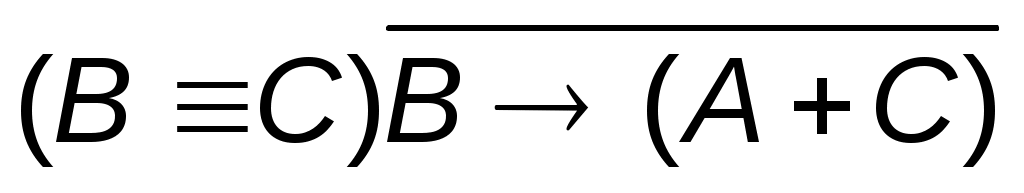
3. 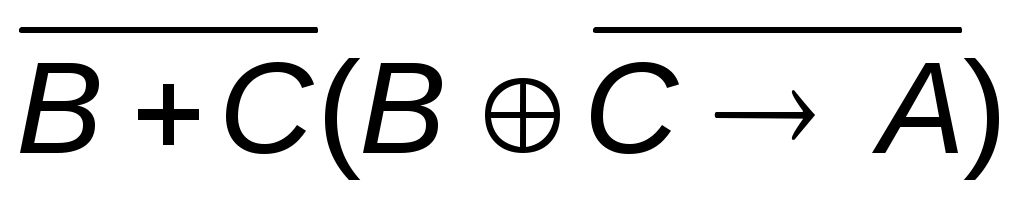 4. 4. 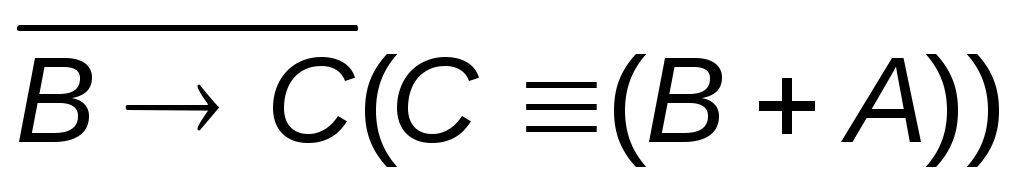
5. 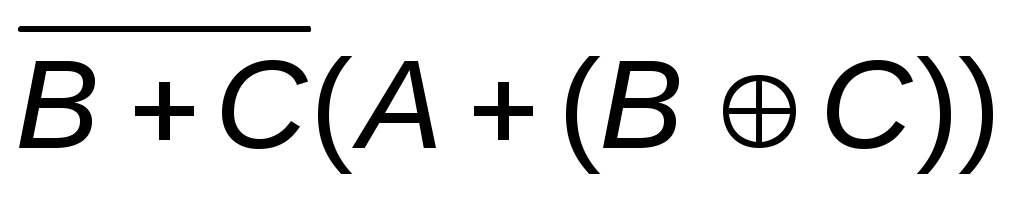
Задание 6. Проверить, не составляя таблицы истинности, являются ли следующие
логические формулы тождественно истинными (тавтологиями).
1. 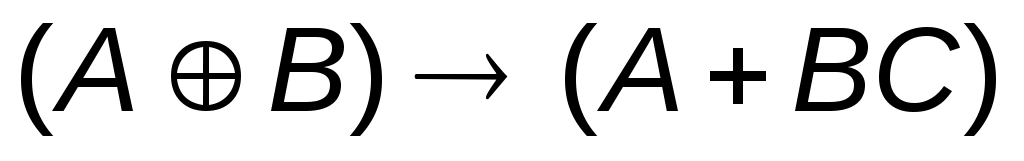 2. 2. 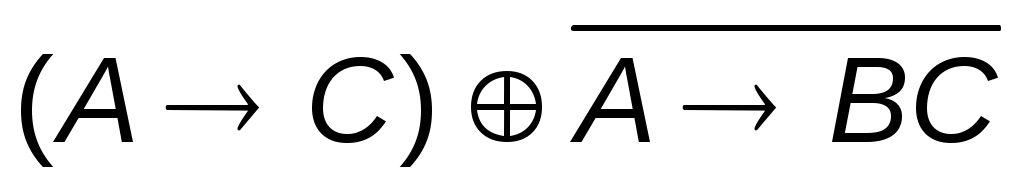
3. 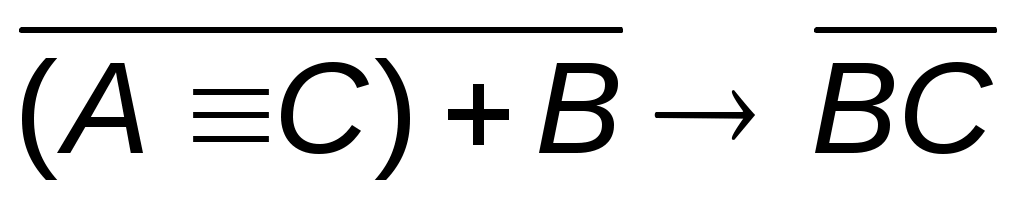 4. 4. 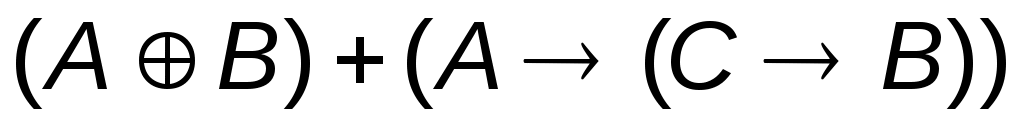
Задание 7. Упростить формулу
1. 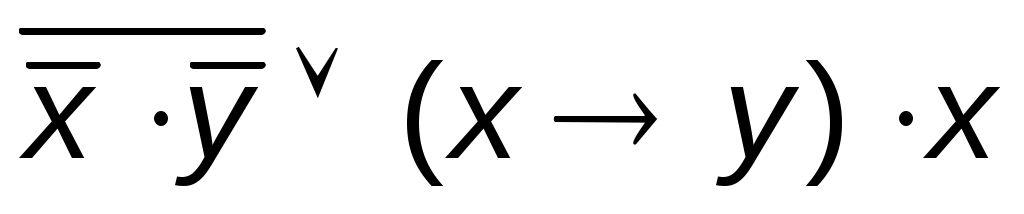
2. 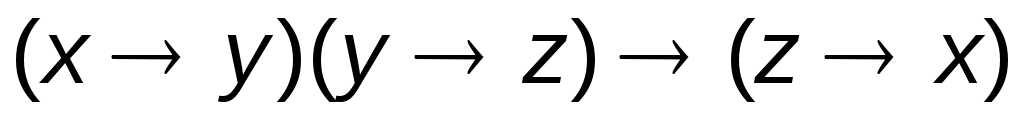
3. 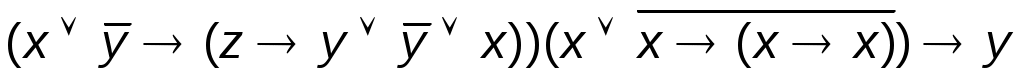
Задание 8. Используя известные правила тождественных преобразований, упростите логические функции и покажите эквивалентность преобразованной функции исходной:
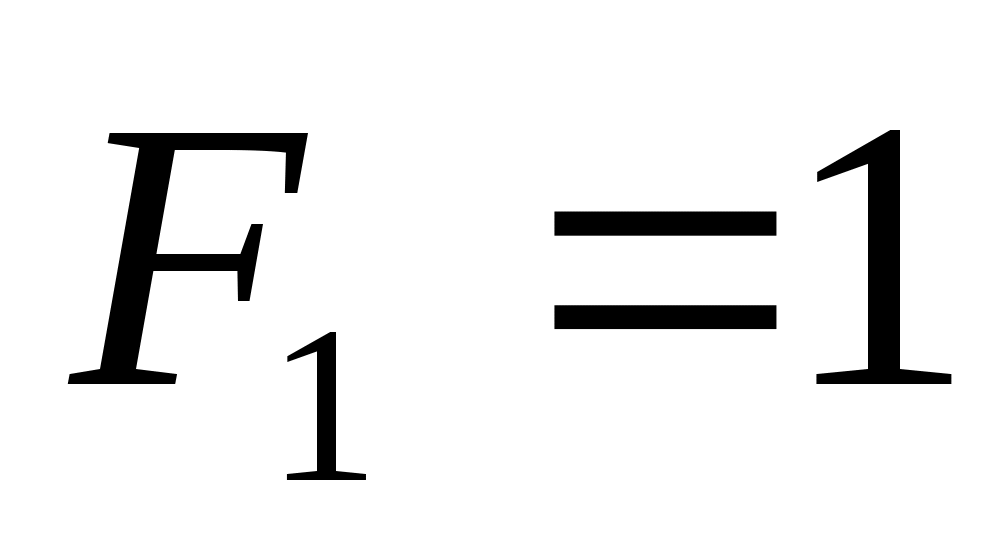 на наборах 3, 5, 6, 7; на наборах 3, 5, 6, 7;
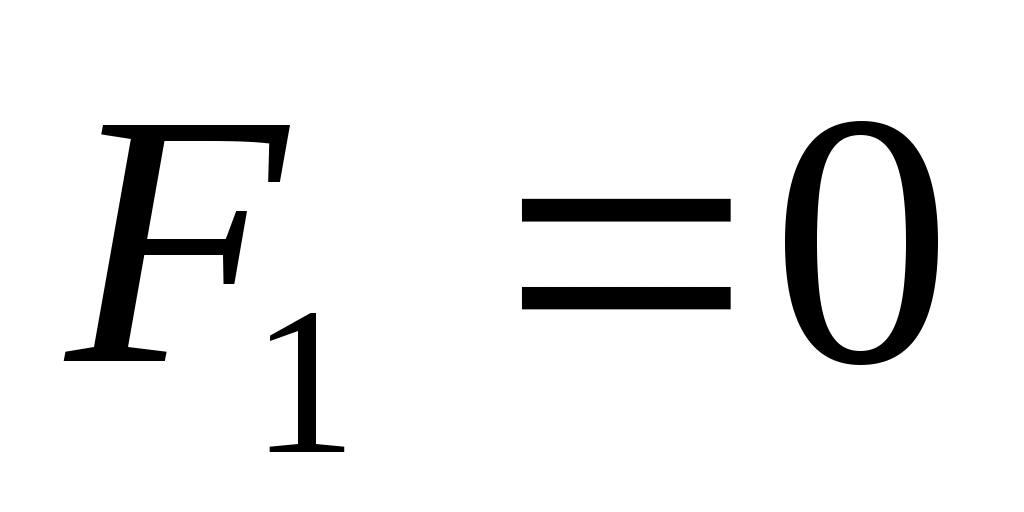 на наборах 1, 3, 4, 5; на наборах 1, 3, 4, 5;
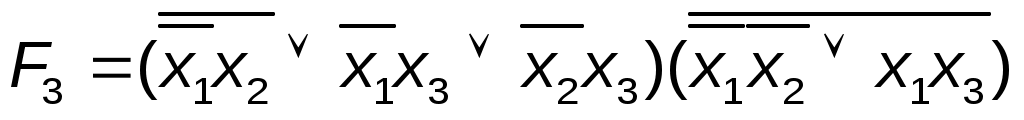 ; ;
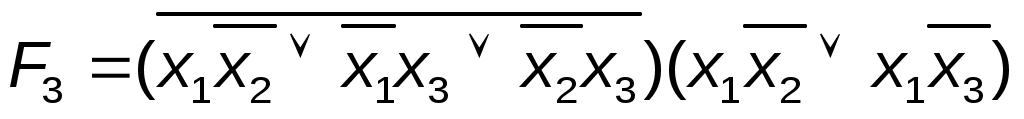 ; ;
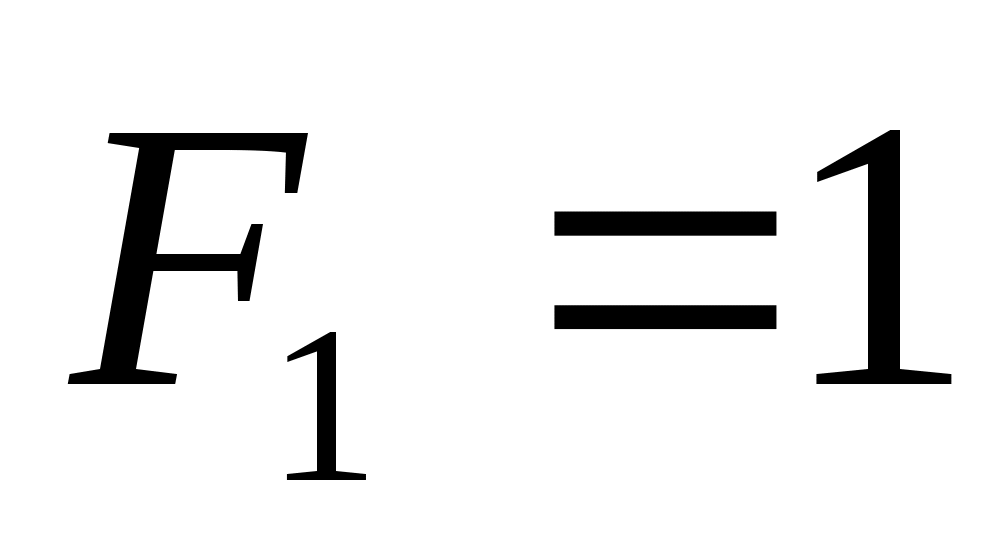 на наборах 3, 5, 6, 7; на наборах 3, 5, 6, 7;
-
x
|
y
|
z
|
F1
|
0
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
-
x
|
y
|
z
|
1
|
2
|
3
|
F
|
0
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
0
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
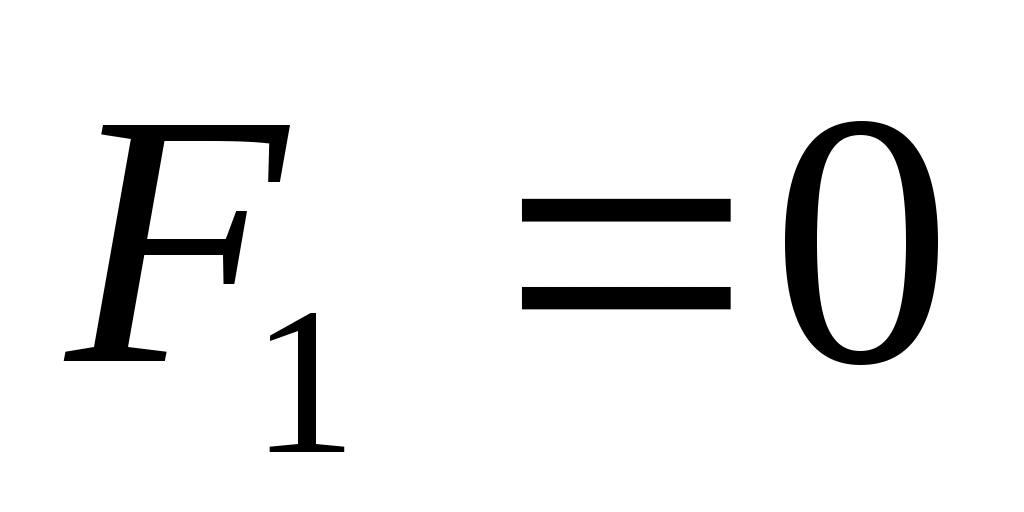 на наборах 1, 3, 4, 5; на наборах 1, 3, 4, 5;
-
x
|
y
|
z
|
F1
|
0
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
-
x
|
y
|
z
|
1
|
2
|
3
|
4
|
5
|
0
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
 Скачать 428.5 Kb.
Скачать 428.5 Kb.