беля. Первообразная Определение
 Скачать 335.26 Kb. Скачать 335.26 Kb.
|
|
Первообразная Определение. Первообразной для функции 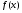 в интервале в интервале 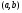 называется функция называется функция 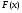 , производная которой равна , производная которой равна 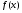 , т.е. , т.е. 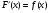 . .Пример. Найти первообразную для функции 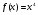 , ,  , так как , так как 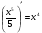 . Легко заметить, что любая функция . Легко заметить, что любая функция  является первообразной для функции является первообразной для функции  , где , где 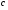 – const. – const.Таким образом, если функция  имеет одну первообразную имеет одну первообразную 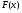 , то , то  имеет бесконечно много первообразных имеет бесконечно много первообразных  т.к. т.к. 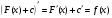 . .Теорема: Если функция  в интервале имеет первообразную в интервале имеет первообразную 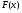 , то любая другая первообразная отличается от данной на константу. , то любая другая первообразная отличается от данной на константу.Определение неопределенного интеграла и его свойства. Определение: Неопределенным интегралом для функции  называют совокупность всех ее первообразных называют совокупность всех ее первообразных  . .Неопределенный интеграл обозначается  . .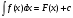 , где , где  какая-либо одна из первообразных для какая-либо одна из первообразных для  . .  называется подынтегральной функцией, называется подынтегральной функцией,  подынтегральным выражением. подынтегральным выражением.Свойства неопределенного интеграла: Доказательство. Пусть  одна из первообразных функции одна из первообразных функции  , тогда , тогда 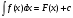 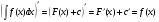 . .Таким образом, действие интегрирования проверяется дифференцированием. Свойство 2 вытекает из свойства 1.

Таблица интегралов. Из определения интеграла и формул дифференцирования функций следуют равенства:
Все формулы проверяются дифференцированием. 1.3. Замена переменной в неопределенном интеграле. Замена переменной в неопределенном интеграле есть действие обратное дифференцированию сложной функции. 2.1. Интегрирование по частям. Интегрирование по частям есть действие обратное дифференцированию произведения. Имеем: 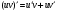 Проинтегрируем обе части равенства: 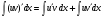  отсюда получаем: отсюда получаем:
Пример  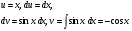 Замечание: Если под знаком интеграла имеем дробь  , числитель которой есть производная знаменателя, то интеграл от этой дроби равен логарифму натуральному от модуля знаменателя!!! , числитель которой есть производная знаменателя, то интеграл от этой дроби равен логарифму натуральному от модуля знаменателя!!!Пример 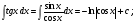 2.2. Интегрирование заменой переменной. Рассмотрим формулу (1) в следующем виде: 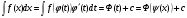 , где , где 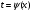 обратная функция для функции обратная функция для функции  . Обратим внимание на то, что при замене переменной . Обратим внимание на то, что при замене переменной  последняя функция должна иметь обратную. последняя функция должна иметь обратную.2.3. Интегрирование рациональных дробей. Разложение правильной дроби на простейшие. Определение: Рациональной дробью называется отношение двух многочленов.  , где , где 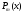 и и 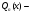 многочлены соответственно степеней m и n. многочлены соответственно степеней m и n.Определение: Рациональная дробь  называется правильной, если степень числителя меньше степени знаменателя, т.е. называется правильной, если степень числителя меньше степени знаменателя, т.е. 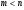 , в противном случае рациональная дробь – неправильная. , в противном случае рациональная дробь – неправильная.Всякая неправильная дробь всегда может быть представлена в виде суммы многочлена и правильной рациональной дроби. Это достигается делением числителя на знаменатель. Отсюда следует, что интегрирование неправильной рациональной дроби всегда можно свести к интегрированию правильной рациональной дроби. В дальнейшем мы покажем, что всякую правильную рациональную дробь можно представить в виде суммы простейших рациональных дробей. К простейшим рациональным дробям относятся дроби: 1) 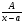 3) 3)  2) 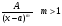 4) 4) 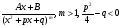 Теорема: Всякую правильную рациональную дробь всегда можно представить в виде суммы простейших рациональных дробей в следующем виде:  где А, В, С с соответствующими индексами – неопределенные коэффициенты. 3. Интегрирование простейших рациональных дробей. Интегрирование тригонометрических выражений. 3.1. Интегрирование простейших рациональных дробей.    Рекуррентная (возвратная формула) 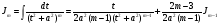 3.2. Интегрирование тригонометрических выражений. Мы будем рассматривать  , где , где  есть рациональная функция от есть рациональная функция от 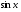 и и 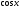 . Т.е. если положить . Т.е. если положить  , a , a 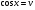 , то , то  есть отношение двух многочленов от есть отношение двух многочленов от  . .Например: 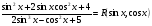 3.2.1. Универсальная подстановка. Интеграл 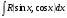 с помощью подстановки с помощью подстановки 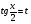 всегда сводится к интегралу от рациональной функции: всегда сводится к интегралу от рациональной функции: 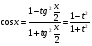  В результате получаем: 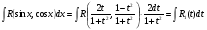 3.2.2. Теперь предположим, что 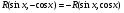 , т.е. подынтегральная функция нечетная относительно , т.е. подынтегральная функция нечетная относительно 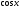 . В этом случае имеем: . В этом случае имеем: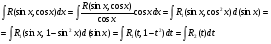 В этом случае была сделана замена 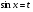 , и вычисление данного интеграла сводится к вычислению интеграла от рациональной функции. , и вычисление данного интеграла сводится к вычислению интеграла от рациональной функции.3.2.3. Пусть  , т.е. подынтегральная функция нечетная относительно , т.е. подынтегральная функция нечетная относительно 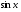 . В этом случае замена . В этом случае замена  сводит вычисление сводит вычисление 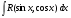 к вычислению интеграла от рациональной функции. к вычислению интеграла от рациональной функции.3.2.4. Теперь рассмотрим тот случай, когда 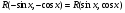 , т.е. подынтегральная функция четная относительно , т.е. подынтегральная функция четная относительно 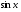 и и 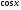 одновременно. В этом случае замена одновременно. В этом случае замена 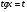 позволяет свести вычисление интеграла позволяет свести вычисление интеграла  к вычислению интеграла от рациональной функции. В самом деле, к вычислению интеграла от рациональной функции. В самом деле,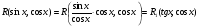 , т.к. , т.к.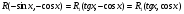 , то функция , то функция  является четной относительно является четной относительно  , поэтому , поэтому 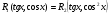 и и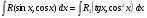 . . В результате замены переменной получим:  Определенный интеграл Определение. Криволинейной трапецией называется фигура, ограниченная прямой l, двумя прямыми, перпендикулярными прямой l и непрерывной кривой, которая расположена по одну сторону от прямой l и любой прямой, перпендикулярной l, пересекается не более чем в одной точке. 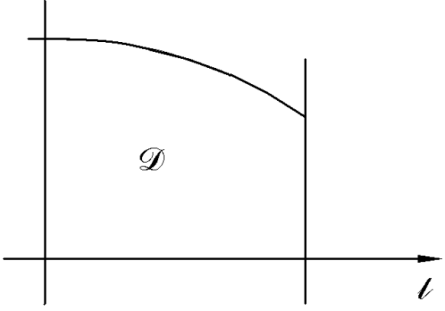 Если прямую l взять за ось OX; OY  OX, тогда определение криволинейной трапеции можно дать следующим образом. OX, тогда определение криволинейной трапеции можно дать следующим образом.Определение. Криволинейной трапецией называется фигура, ограниченная осью OX, прямыми x=a; x=b и графиком непрерывной функции  , ,  . .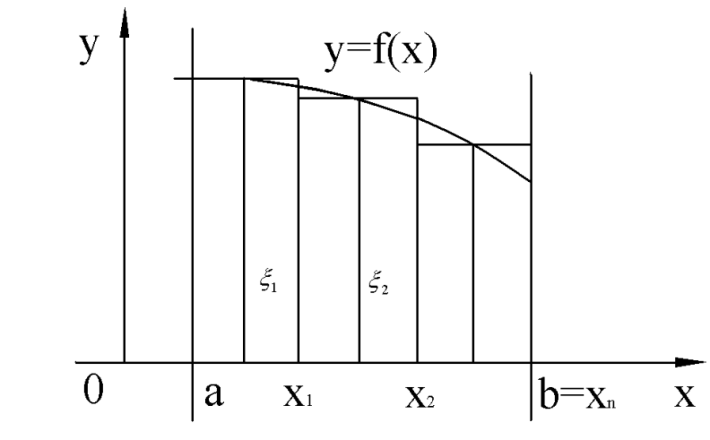 Определение определенного интеграла Определение. Конечный предел интегральных сумм при  называется определенным интегралом от функции называется определенным интегралом от функции 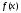 на отрезке [a,b]. на отрезке [a,b].Определенный интеграл обозначается следующим образом: 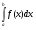 . .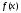 называется подынтегральной функцией, называется подынтегральной функцией, 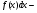 подынтегральным выражением, подынтегральным выражением,  – пределы интегрирования, а – нижний, b – верхний предел интегрирования. – пределы интегрирования, а – нижний, b – верхний предел интегрирования.Определение определенного интеграла можно записать в следующем виде: 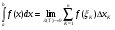 , ,если последний предел существует. Геометрический смысл определенного интеграла. Если подынтегральная функция 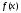 непрерывна и неотрицательна на отрезке непрерывна и неотрицательна на отрезке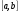 , то , то 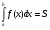 есть площадь соответствующей криволинейной трапеции. есть площадь соответствующей криволинейной трапеции.Механический смысл определенного интеграла. Если подынтегральная функция непрерывна и неотрицательна на 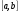 , то , то 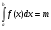 есть масса неоднородного стержня есть масса неоднородного стержня 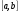 с плотностью с плотностью 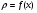 . .5.3. Теорема существования определенного интеграла. Если 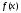 непрерывна на отрезке непрерывна на отрезке 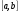 , то , то 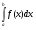 существует. существует.5.4. Свойства определенного интеграла. 1)  2) 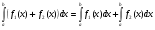 3) Постоянный множитель можно выносить за знак интеграла. 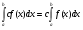 , с=const. , с=const.4) 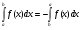 5) 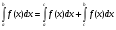 6) 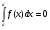 7) Если 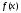 знакопостоянна на знакопостоянна на 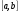 , то , то 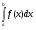 имеет тот же знак, что и имеет тот же знак, что и 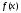 . .8) Если  , ,  , то , то  . .9) Теорема об оценке интеграла. 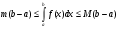 , где m и M – соответственно наименьшее и наибольшее значения , где m и M – соответственно наименьшее и наибольшее значения 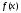 на на 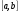 . .Замечание: свойства 2, 3, 4, 5, 7, 8, 9 справедливы, если соответствующие интегралы существуют. 10) Теорема о среднем. Если 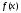 непрерывна на непрерывна на 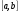 , то существует точка , то существует точка  , для которой справедливо равенство , для которой справедливо равенство 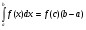 . .Формула Ньютона-Лейбница. Теорема. Справедлива формула 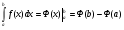 , где Ф(x) какая-либо первообразная для подынтегральной функции , где Ф(x) какая-либо первообразная для подынтегральной функции 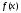 . .6.4. Замена переменной в определенном интеграле. Пусть  непрерывна на отрезке непрерывна на отрезке 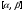 и и  , а функция , а функция 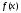 непрерывна на отрезке непрерывна на отрезке 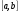 . .Справедлива формула  . .9.1.1. Пусть некоторая кривая является графиком функции  , , 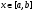 , для которой , для которой 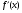 является непрерывной функцией на является непрерывной функцией на 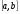 . Такие кривые называются гладкими. . Такие кривые называются гладкими.ДИФ УРАВНЕНИЯ Определение . Дифференциальным уравнением называется уравнение, содержащее независимую переменную, неизвестную функцию и производные неизвестной функции. Дифференциальное уравнение в общем виде можно записать следующим образом: 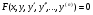 , где , где  -независимая переменная, -независимая переменная, 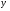 -неизвестная функция. Решить диф. Уравнение значит найти неизв. Функцию. -неизвестная функция. Решить диф. Уравнение значит найти неизв. Функцию.Определение . Порядком дифференциальнрого уравнения называется наивысший порядок производной, входящей в уравнение. Например: 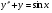 является дифференциальным уравнением 2го порядка. является дифференциальным уравнением 2го порядка.Определение . Функция 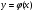 называется решение дифуравнения, если при подстановке функции и ее соответствующих производных в уравнение, уравнение обращается в тождество. называется решение дифуравнения, если при подстановке функции и ее соответствующих производных в уравнение, уравнение обращается в тождество.12. Дифференциальные уравнения 1го порядка. В общем виде дифференциальное уравнение первого порядка записывается следующим образом: 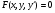 . . В частных случаях в левую часть уравнения в явном виде могут не входить  и и 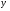 , но обязательно должна входить производная , но обязательно должна входить производная  . .КОШИ Теорема Коши: Если функция  и ее частная производная и ее частная производная  непрерывны в некоторой области, содержащей внутри точку непрерывны в некоторой области, содержащей внутри точку 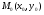 , то уравнение , то уравнение  имеет единственное решение, удовлетворяющее начальному условию имеет единственное решение, удовлетворяющее начальному условию 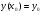 , в некотором интервале , в некотором интервале  , т.е. задача Коши имеет единственное решение. , т.е. задача Коши имеет единственное решение.Определение . Любое решение задачи Коши называется частным решением дифуравнения. Определение . Совокупность всех частных решений дифуравнения называется общим решением этого уравнения. Задача Коши: Найти решение дифуравнения  , которое удовлетворяет начальному условию , которое удовлетворяет начальному условию 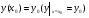 . .Определение . Дифференциальное уравнение называется разрешимым в квадратурах, если его общее решение может быть получено с помощью конечного числа операций интегрирования. 12.2. Дифуравнение с разделяющимися переменными. Определение . Уравнение вида 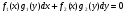 называется уравнением с разделяющимися переменными. называется уравнением с разделяющимися переменными.Для решения дифуравнения с разделяющимися переменными надо разделить переменные и проинтегрировать. 1.  - решение данного уравнения, т.к. - решение данного уравнения, т.к. 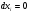 , , 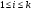 . .2. 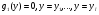 - решение данного уравнения, т.к. - решение данного уравнения, т.к.  , , 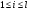 . .3. 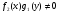 . .Разделив обе части равенства на  , получим: , получим: 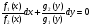 , т.е. первое слагаемое зависит только от , т.е. первое слагаемое зависит только от  , а второе слагаемое только от , а второе слагаемое только от 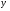 , в этом и заключается разделение переменных. Интегрируя последнее равенство, получим , в этом и заключается разделение переменных. Интегрируя последнее равенство, получим  . Таким образом, любое дифуравнение с разделяющимися переменными интегрируется в квадратурах. . Таким образом, любое дифуравнение с разделяющимися переменными интегрируется в квадратурах.12.3. Однородные дифуравнения первого порядка. Определение . Дифференциальное уравнение вида 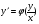 называется однородным. называется однородным.Это уравнение с помощью замены 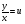 сводится к решению дифуравнения с разделяющимися переменными. Действительно, сводится к решению дифуравнения с разделяющимися переменными. Действительно, 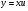 , ,  12.4. Линейные дифференциальные уравнения первого порядка. Определение . Дифференциальное уравнение вида:  , ,  . (16) . (16)называется линейным уравнением. Решение линейного уравнения можно искать в виде: 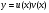 , ,  . Значения для . Значения для 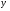 и и  подставим в данное уравнение. В результате получим тождество: подставим в данное уравнение. В результате получим тождество:  12.5 Уравнения Бернулли Определение . Уравнение вида  называется уравнением Бернулли. Если  , то уравнение является линейным. Если , то уравнение является линейным. Если 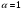 , то уравнение является уравнением с разделяющимися переменными. , то уравнение является уравнением с разделяющимися переменными.Решение уравнения Бернулли можно искать в виде  и решать это уравнение аналогично решению линейного уравнения. и решать это уравнение аналогично решению линейного уравнения.13. Дифференциальные уравнения 2го порядка. В общем случае дифуравнение 2го порядка имеет вид:  Если уравнение разрешено относительно второй производной, то оно имеет следующий вид: 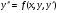 . .13.1. Задача Коши для уравнения 2го порядка. Теорема Коши о существовании и единственности решения задачи Коши. Задача Коши: Найти решение уравнения 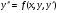 , удовлетворяющее начальным условиям: , удовлетворяющее начальным условиям: 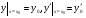 . .Теорема Коши: Если  непрерывна вместе с частными производными непрерывна вместе с частными производными  в некоторой окрестности точки в некоторой окрестности точки 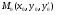 , то уравнение , то уравнение 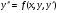 имеет единственное решение в некотором промежутке имеет единственное решение в некотором промежутке 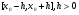 , которое удовлетворяет начальным условиям , которое удовлетворяет начальным условиям 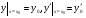 , т.е. задача Коши имеет единственное решение. (Без доказательства). , т.е. задача Коши имеет единственное решение. (Без доказательства).Определение . Всякое решение задачи Коши называется частным решением дифуравнения. Определение . Совокупность всех частных решений называется общим решением дифуравнения. Общее решение дифуравнения 2го порядка зависит от двух произвольных постоянных. 13.2. Дифуравнения 2го порядка, допускающие понижение порядка. 13.2.1. Рассмотрим уравнение вида: 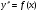 . Так как . Так как 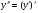 , то , то 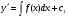 , а , а 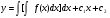 . .решение, получим искомое частное решение 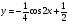 . .13.2.2. Уравнение не содержит в явном виде 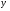 , т.е. уравнение имеет вид , т.е. уравнение имеет вид 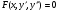 . Сделаем замену: . Сделаем замену: 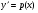 , тогда , тогда  . В результате замены получим уравнение первого порядка относительно неизвестной функции . В результате замены получим уравнение первого порядка относительно неизвестной функции  . .13.2.3. Уравнение не содержит в явном виде  , т.е. уравнение имеет вид: , т.е. уравнение имеет вид:  В этом случае делается замена 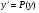 , ,  14. Линейные дифференциальные уравнения второго порядка . Уравнение вида 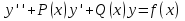 (21) (21) называется линейным уравнением второго порядка. Если f(x)= 0, то уравнение (21) называется однородным, если же f(x) ≠0, то уравнение (21) называется неоднородным. Линейный дифференциальный оператор второго порядка.Определение. Оператором Aиз множества Х во множество Y называется соответствие, которое по определенному закону каждому элементу х ϵ Х сопоставляет однозначно элемент А(х) ϵ Y. Множество Х называется областью определения оператора А и обозначается D(A), множество { A(x), х ϵ Х } называется областью значений оператора и обозначается R(A). Часто вместо А(х) пишут Ах. Определение. Оператор А(х) называется линейным, если А(α  +β +β )=αА( )=αА( )+βА( )+βА( ) )  x1, x2 x1, x2 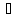 X и X и 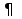 α1, α2 α1, α2  Определение. Оператор L(y)= 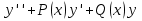 называется дифференциальным оператором второго порядка. называется дифференциальным оператором второго порядка.
 (23) (23)Уравнение (23) можно записать в виде L(y)=0 . Легко видеть, что функция 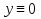 является решением уравнения (23), это решение называется тривиальным. Естественно, интерес представляют нетривиальные решения. является решением уравнения (23), это решение называется тривиальным. Естественно, интерес представляют нетривиальные решения.Теорема. Если 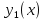 и и 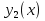 – два решения L(y)=0, то их линейная комбинация – два решения L(y)=0, то их линейная комбинация 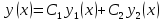 также является решением уравнения L(y)=0 ,где также является решением уравнения L(y)=0 ,где 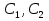 –произвольные постоянные. –произвольные постоянные.Основная теорема о структуре общего решения линейного однородного дифференциального уравнения 2-го порядка.Определение. Система функций 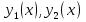 называется линейно зависимой в промежутке E, если существуют числа называется линейно зависимой в промежутке E, если существуют числа 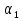 , , одновременно не равные нулю, такие что одновременно не равные нулю, такие что   , в противном случае система функций , в противном случае система функций  , , называется линейно независимой. называется линейно независимой.Определение. Линейно независимая система решений 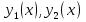 уравнения (23) называется фундаментальной системой решений. уравнения (23) называется фундаментальной системой решений.Теорема. Для того, чтобы система решений 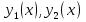 уравнения (3) была фундаментальной необходимо и достаточно , чтобы отношение уравнения (3) была фундаментальной необходимо и достаточно , чтобы отношение 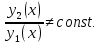 Определитель Вронского и его свойства.Определителем Вронского или кратко вронскианом системы двух частных решений 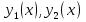 уравнения (23) называется функциональный определитель уравнения (23) называется функциональный определитель 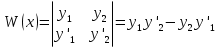 Теорема. Если 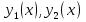 не образуют фундаментальную систему решений уравнения (3),то не образуют фундаментальную систему решений уравнения (3),то  . .Теорема. Если  , то , то 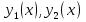 не образуют фундаментальную систему решений. не образуют фундаментальную систему решений.Теорема. Вронскиан двух частных решений тождественно равен нулю тогда и только тогда, когда система решений 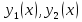 - не является фундаментальной. - не является фундаментальной.Формула Остроградского-Лиувилля.Пусть 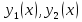 два частных решения Л.О.Д.У. (3), в котором функция Р(х) предполагается непрерывной в некотором промежутке, тогда два частных решения Л.О.Д.У. (3), в котором функция Р(х) предполагается непрерывной в некотором промежутке, тогда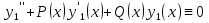  W(x)=W(x0)  Полученная формула называется формулой Остроградского-Лиувилля. Существование фундаментальной системы решений Л.О.Д.У.(23).Теорема. Каждое ЛО.Д.У.(3) имеет фундаментальную систему решений 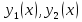 . .Основная теорема о структуре общего решения Л.О.Д.У.Теорема. Общее решение Л.О.Д.У. может быть записано в виде линейной комбинации фундаментальной системы решений y1(х) и у2(х), т.е. у=с1у1(х)+с2у2(х) Решение уравнения будем искать в виде y= 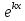 . Для этого найдем y’=k . Для этого найдем y’=k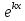 , ,
Данное уравнение имеет вид: y”+ay’+by=0, где a и b действительные числа. y”=  и подставим в данное уравнение: и подставим в данное уравнение: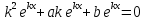 . Так как . Так как 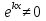 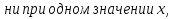  . .Последнее уравнение называется характеристическим уравнением для данного Л.О.Д.У. Возможны следующие три случая:
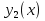 = = = = =x =x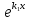 , т.к. по теореме Виетта сумма корней приведенного квадратного уравнения равна коэффициенту при k с противоположным знаком, т.е. 2k1=-a и 2k1+a=0. Таким образом, общее решение уравнения запишется в виде: y(x)= , т.к. по теореме Виетта сумма корней приведенного квадратного уравнения равна коэффициенту при k с противоположным знаком, т.е. 2k1=-a и 2k1+a=0. Таким образом, общее решение уравнения запишется в виде: y(x)=
В этом случае мы получаем два частных решения  , ,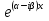 . .Неудобство состоит в том, что оба решения записаны в комплексной форме, а мы хотим найти общее решение в действительной форме. Мы применим формулы Эйлера  , , 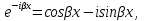 которые примем без доказательства. которые примем без доказательства.По теореме 2 функции y1(x)=  = = = = = = 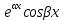 и y2(x) = и y2(x) = = =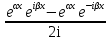 = = 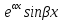 тоже являются решениями данного уравнения, которые образуют фундаментальную систему решений, т.к. тоже являются решениями данного уравнения, которые образуют фундаментальную систему решений, т.к.  . Поэтому общее решение запишется в виде: . Поэтому общее решение запишется в виде:y=  Пример 3. Решить уравнение y”+3y’-4y=0 Решение. Составим характеристическое уравнение k2+3k-4=0. Корнями уравнения являются k1=-4, k2=1, y(x)=c1 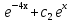 . .Пример 4. Решить уравнение y”-2y’+y=0 Решение. K2-2k+1=0, k1,2=1, y(x)=  . .Пример 5. Решить уравнение y”+y=0. Решение. K2+1=0, k2=-1, k1,2=±i, α=0, β=1. y(x)=  . .
Уравнение вида: 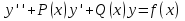 ; L(y) =f(x) (26) ; L(y) =f(x) (26)где f(x)≠0 называется линейным неоднородным дифференциальным уравнением второго порядка (Л.Н.Д.У.). Основная теорема о структуре общего решения Л.Н.Д.У.Теорема. Общее решение линейного неоднородного дифференциального уравнения может быть представлено в виде суммы общего решения соответствующего однородного уравнения и некоторого частного решения данного неоднородного решения, т.е. y(x) =  + y*(x) , где + y*(x) , где  - общее решение соответствующего однородного уравнения L(y) = 0, а y*(x) – частное решение данного уравнения L(y) = f(x). - общее решение соответствующего однородного уравнения L(y) = 0, а y*(x) – частное решение данного уравнения L(y) = f(x).Метод вариации произвольных постоянных (метод Лагранжа) нахождения частного решения линейного неоднородного дифференциального уравнения.Общее решение линейного неоднородного дифференциального уравнения имеет вид: y(x) = 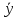 (x) + y*(x), где (x) + y*(x), где 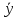 (x) - есть общее решение соответствующего однородного уравнения y” + P(x)y’ + Q(x)y = 0, а y*(x) есть частное решение данного неоднородного уравнения y” + P(x)y’ + Q(x)y = f(x). (x) - есть общее решение соответствующего однородного уравнения y” + P(x)y’ + Q(x)y = 0, а y*(x) есть частное решение данного неоднородного уравнения y” + P(x)y’ + Q(x)y = f(x).Будем предполагать, что 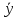 (x) известно, т.е. (x) известно, т.е. 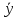 (x) = C1y1(x) + C2y2(x), где y1(x) и y2(x) образуют фундаментальную систему решений Л.О.Д.У., а C1 и C2 – произвольные постоянные. (x) = C1y1(x) + C2y2(x), где y1(x) и y2(x) образуют фундаментальную систему решений Л.О.Д.У., а C1 и C2 – произвольные постоянные. Метод подбора частного решения Л.Н.Д.У. 2-го порядка с постоянными коэффициентами и специальной правой частью.Решение линейного неоднородного дифференциального уравнения 2-го порядка с постоянными коэффициентами и специальной правой частью 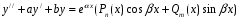 где а-const,b-const, Pn(x) и Qm(x)-многочлены соответственно степеней n и m. Общее решение такого уравнения записывается в виде y=ȳ(x)+y*(x), где ȳ(x) – общее решение соответствующего однородного уравнения y’’ + + ay’ + by = 0. Решение такого уравнения рассмотрено в п.1.3.5. Частное решение данного неоднородного уравнения ищется в виде: y*(x) =x ͬ eαx(Qs(1) (x) cos βx + Qs(2)(x) sin βx), где r – кратность чисел α±β как корня характеристического уравнения k² + ak + b = 0, s= max(n,m), Qs(1) (x) и Qs(2)(x) – многочлены степени s с неопределенными коэффициентами. Теорема о наложении частных решений.Пусть дано линейное неоднородное дифференциальное уравнение вида:  Если y*1(x) есть частное решение уравнения  , (27) , (27)а y*2(x) есть частное решение уравнения  , (28) , (28)то y*(x)= y*1(x)+ y*2(x) есть частное решение данного уравнения. ЛОДУn-го порядка с постоянными коэффициентами Рассмотрим уравнение (2): Его характеристическое уравнение имеет вид: |



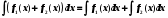 .
.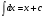



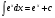


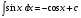
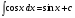
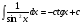
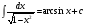

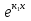 , у2(х)=
, у2(х)= , которые образуют фундаментальную систему решений, т.к.
, которые образуют фундаментальную систему решений, т.к.  =
=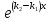 ≠0. Общее решение имеет вид: y=C1
≠0. Общее решение имеет вид: y=C1