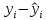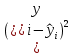Контрольная работа. Колесникова. Планирование и организация эксперимента в сфере безопасности
 Скачать 73.1 Kb. Скачать 73.1 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ Кузбасский гуманитарно-педагогический институт федерального государственного бюджетного образовательного учреждения высшего образования «Кемеровский государственный университет» КГПИ ФГБОУ ВО «КемГУ» Факультет физической культуры, естествознания и природопользования Кафедра геоэкологии и географии КОНТРОЛЬНАЯ РАБОТА по дисциплине «Планирование и организация эксперимента в сфере безопасности» Выполнил: студент 3 курса группы ТБ-з-19-1 ФИО Колесникова Надежда Михайловна Проверил: Доцент каф. ГГ Чмелева Ксения Владимировна ___________________________________ подпись Работа защищена с оценкой «___________» удовлетв., хорошо, отлично Общий балл: ___________ «__» ___________ 2022 г. Новокузнецк, 2022 Содержание Введение 3 1.Регрессионный анализ 4 2.Практическая часть 8 Заключение 17 Список литературы 18 Приложение 1 Критические точки критерия Кохрена 19 Приложение 2 Критические точки критерия Фишера 20 Приложение 3 Критические точки критерия Стьюдента 21 Введение Целью работы было - закрепление полученных теоретических знаний и практических навыков. В процессе выполнения контрольной работы решаются следующие задачи: систематизация, углубления и закрепление теоретических знаний в соответствии с заданной темой; формирование умений применять теоретические знания при решении поставленных вопросов; формирование умений использовать справочную; самостоятельности, ответственности и организованности; развитие навыков оформления письменных работ. 1 Регрессионный анализ Наиболее распространенным способом обработки экспериментальных данных является так называемый метод регрессионного анализа, в частности такой его вариант, который включает: использование метода наименьших квадратов; отражение неизвестной функции истинного отклика ϕ(х), "спрятанной" в таблице экспериментальных данных, алгебраическим степенным полиномом η(х,b) [3],[10]. Метод регрессионного анализа применим при соблюдении следующих условий: 1) массив значений откликов объекта исследования на данной g-строке имеет нормальное распределение с математическим ожиданием; 2) дисперсии для g=1,2,3,…,n равны. Поскольку дисперсия наблюдения характеризует точность, с которой мы получаем наблюдения, постольку опыты при g=1,2,3,…,n равноточные, т.е. эксперимент воспроизводится при разных наблюдениях с одинаковой точностью; 3) результаты наблюдения отклика уg и их ошибки δg в различных опытах независимы, т.е. µ11{yjyq} и µ11{δjδq} равны нулю; 4) независимые от отклика факторы воздействия на объект х и производные от них базисные функции f(х) определяются в эксперименте без ошибок в силу двух факторов: - в случае наличия таких ошибок они "стекают" на отклик объекта, увеличивая рассеивание облака экспериментальных точек; - влияние этих ошибок на рассеивание облака точек пренебрежительно мало по сравнению с влиянием шума; 5) векторы факторов воздействия на объект х и векторы производных 16 от них базисных функций f(х) линейно-независимы, т.е. ни один вектор нельзя получить как линейную комбинацию других. В противном случае определители производных от них матриц будут равны нулю и матричные расчеты станут невозможны; 6) математическая модель отклика объекта исследования η(х,β) адекватна функции ϕ(х) и, таким образом, η(х,β) = ϕ(х). [4] Сформированная таким образом задача носит название задачи регрессии, эксперимент называется регрессионным, уравнения (полиномы) – уравнениями (полиномами) регрессии, а сам метод решения называется регрессионным анализом. Этот термин отражает тот факт, что с увеличением степени полинома, т.е. с увеличением количества его членов, в общем случае ошибка уравнения уменьшается – "регрессирует"[5]. Процедура регрессионного анализа включает: нахождение уравнения регрессии; статистический анализ качества уравнений регрессии[2]. Различают линейную и нелинейную модель парной регрессии [4], [8]. Пример выполнения парного корреляционного и регрессионного анализа определить коэффициент корреляции между твердостью y и степенью деформации x. При наличии взаимосвязи определить уравнение регрессии и его адекватность экспериментальным результатам. Таблица 1 Парный корреляционный и регрессионный анализ
Продолжение таблицы 1
Определяют коэффициент корелляции: 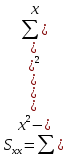 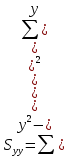 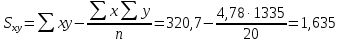 Тогда, коэффициент корреляции 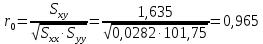 Проводят проверку коэффициента корреляции. Для этого выбирают α=0,01 и определяют число степеней свободыуровень значимости Ф = n-2 = 20 – 2 = 18. По таблице проверки коэффициента корреляции на значимость относительно нуля определяют rф,α= r18;0,01 = 0,561. Поскольку r0> rф,α , то r обладает высокой степенью значимости. Определяют коэффициент уравнения регрессии. 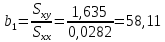 Для определения b0 определяют средние арифметические значения 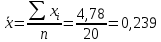 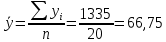 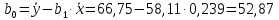 Тогда уравнение регрессии имеет вид: 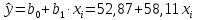 Определяют адекватность уравнения экспериментальным данным: 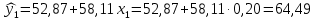 ………………………………………………..... 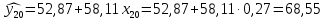 Определяют общую и остаточную дисперсию  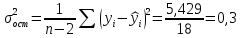 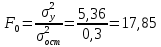 Так как F0=17,85 >Fn-1;n-2;0,05, то следует признать, что уравнение адекватно описывает экспериментальные результаты.[5],[9]. 2 Практическая часть Постановка задачи Циклон - установка для сухой механической очистки газов от твердых или жидких частиц, которые делятся на пыль, дым и туман, выделяющихся при различных технологических процессах, связанных с сушкой, обжигом, сжиганием топлива. Эффективность очистки определяется коэффициентом полезного действия (КПД) циклона, который зависит от ряда факторов в зависимости от его типа. Рассчитать полным факторным экспериментом влияние некоторых наиболее значимых факторов на КПД циклона. Таблица 1 - Значения факторов
Таблица 2 - Функция отклика
Алгоритм построения полного факторного эксперимента и оценки влияния факторов Определение центра плана (основной уровень) и уровня варьирования факторов Находим центр плана: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||