Описание контрольных измерительных материалов для осуществления оценки качества образования по математике обучающихся 9 классов
Назначение работы
Контрольные измерительные материалы (КИМ) в виде итоговой диагностической работы позволяют осуществить оценку предметных знаний по математике обучающихся за 9-й класс.
Данная диагностическая работа может быть использована при проведении оценочных процедур на уровне образовательной организации.
2. Документы, определяющие содержание работы
Содержание и структура итоговой диагностической работы по математике за 9 класс определяются на основе Обязательного минимума содержания основных образовательных программ и Требований к уровню подготовки выпускников основной школы (приказ Минобразования России от 05.03.2004 № 1089 «Об утверждении федерального компонента государственных стандартов начального общего, основного общего и среднего (полного) общего образования»).
Задания КИМ ориентированы на следующие учебники по математике, используемые при обучении в 9 классе и включённые в Федеральный перечень Минобрнауки РФ на 2021–2022 учебный год: Алгебра. 9 класс. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б, «Геометрия для 7-9 классов» Атанасяна Л.С., Бутузова В.Ф., Кадомцева С.Б. и др.
3. Кодификаторы проверяемых элементов содержания и требований к уровню подготовки участников
Таблица1. Кодификатор проверяемых элементов содержания
Код
раздела
|
Код элемента
|
Проверяемые элементы содержания
|
1
|
|
Числа и вычисления
|
|
1.1
|
Числовые выражения, порядок действий в них, использование
скобок. Законы арифметических действий.
|
|
1.2
|
Сравнение действительных чисел
|
|
1.3
|
Степень с целым показателем
|
|
1.4
|
Квадратный корень из числа
|
|
1.5
|
Корень n-ой степени
|
2
|
|
Алгебраические выражения
|
|
2.1
|
Буквенные выражения. Числовое значение буквенного выражения
|
|
2.2
|
Допустимые значения переменных, входящих в алгебраические выражения
|
|
2.3
|
Равенство буквенных выражений, тождество. Преобразования выражений
|
|
2.4
|
Квадратный трехчлен. Теорема Виета. Разложение квадратного
трехчлена на линейные множители
|
|
2.5
|
Степень и корень многочлена с одной переменной
|
|
2.6
|
Алгебраическая дробь. Сокращение дробей
|
|
2.7
|
Рациональные выражения и их преобразования
|
|
2.8
|
Свойства квадратных корней и их применение в вычислениях
|
3
|
|
Уравнения и неравенства
|
|
3.1
|
Решение рациональных уравнений
|
|
3.2
|
Примеры решения уравнений высших степеней. Решение уравнений методом замены переменной. Решение уравнений методом разложения на множители.
|
|
3.3
|
Система уравнений 1 и 2 степени с двумя переменными. Решение подстановкой и алгебраическим сложением. Графический способ решения системы уравнений
|
|
3.4
|
Уравнение с несколькими переменными
|
4
|
|
Неравенства
|
|
4.1
|
Неравенства второй степени и способы их решения (метод интервалов, с помощью графика квадратичной функции)
|
|
4.2
|
Системы неравенств с двумя переменными
|
5
|
|
Текстовые задачи
|
|
5.1
|
Решение текстовых задач арифметическим способом
|
|
5.2
|
Решение текстовых задач помощью рациональных уравнений и систем уравнений
|
|
5.3
|
|
6
|
|
Числовые последовательности
|
|
6.1
|
Понятие последовательности
|
|
6.2
|
Арифметическая прогрессия. Формула общего члена
арифметической прогрессии
|
|
6.3
|
Формула суммы первых нескольких членов арифметической
прогрессии
|
|
6.4
|
Геометрическая прогрессия. Формула общего члена
геометрической прогрессии
|
|
6.5
|
Формула суммы первых нескольких членов геометрической
прогрессии
|
|
6.6
|
Сложные проценты
|
7
|
|
Функции
|
|
7.1
|
Понятие функции. Область определения функции. Способы
задания функции
|
|
7.2
|
График функции, возрастание и убывание функции, наибольшее и
наименьшее значения функции, нули функции, промежутки
знакопостоянства, чтение графиков функций
|
|
7.3
|
Квадратичная функция, её график. Парабола. Координаты
вершины параболы, ось симметрии
|
|
7.4
|
Использование графиков функций для решения уравнений и
систем
|
8
|
|
Координаты на прямой и плоскости
|
|
8.1
|
Декартовы координаты на плоскости; координаты точки
|
|
8.2
|
Координаты середины отрезка
|
|
8.3
|
Формула расстояния между двумя точками плоскости
|
|
8.4
|
Уравнение окружности
|
|
8.5
|
Графическая интерпретация уравнений с двумя переменными и
их систем
|
9
|
|
Геометрия
|
|
9.1
|
Преобразования плоскости. Движения. Симметрия
|
|
9.2
|
Зависимость между величинами сторон и углов треугольника
|
|
9.3
|
Синус, косинус, тангенс острого угла прямоугольного треугольника и углов от 00 до 1800
|
|
9.4
|
Решение прямоугольных треугольников. Основное тригонометрическое тождество. Теорема косинусов и теорема синусов
|
|
9.5
|
Длина окружности. Площади круга и сектора.
|
|
9.6
|
Вписанные и описанные окружности правильного многоугольника
|
|
9.7
|
Площади многоугольников.
|
|
9.8
|
Вектор, длина (модуль) вектора
|
|
9.9
|
Операции над векторами (сумма векторов, умножение вектора на число)
|
|
9.10
|
Угол между векторами
|
|
9.11
|
Коллинеарные векторы, разложение вектора по двум
неколлинеарным векторам
|
|
9.12
|
Координаты вектора
|
|
9.13
|
Скалярное произведение векторов
|
10
|
10.1
|
Статистика и теория вероятностей
|
|
10.2
|
Представление данных в виде таблиц, диаграмм, графиков
|
|
10.3
|
Средние результатов измерений
|
|
10.4
|
Частота события, вероятность
|
|
10.5
|
Равновозможные события и подсчёт их вероятности
|
|
10.6
|
Представление о геометрической вероятности
|
|
10.7
|
Решение комбинаторных задач: перебор вариантов,
комбинаторное правило умножения
|
Таблица 2. Кодификатор требования к уровню подготовки участников
Код
|
Код контролируемого умения
|
Требования (умения), проверяемые заданиями
диагностической итоговой работы
|
1
|
|
Уметь выполнять вычисления и преобразования
|
1.1
|
Выполнять, сочетая устные и письменные приёмы, арифметические
действия с рациональными числами, сравнивать действительные
числа; находить в несложных случаях значения степеней с целыми
показателями и корней; вычислять значения числовых выражений;
переходить от одной формы записи чисел к другой
|
1.2
|
Решать текстовые задачи, включая задачи, связанные с отношением,
пропорциональностью величин, дробями, процентами
|
1.3
|
Изображать числа точками на координатной прямой
|
2
|
|
Уметь выполнять преобразования алгебраических выражений
|
2.1
|
Составлять буквенные выражения и формулы по условиям задач, находить значения буквенных выражений, осуществляя необходимые подстановки и преобразования
|
2.2
|
Выполнять основные действия со степенями с целыми показателями,
с многочленами и алгебраическими дробями
|
2.3
|
Выполнять разложение многочленов на множители
|
2.4
|
Применять свойства арифметических квадратных корней для преобразования числовых выражений, содержащих квадратные корни
|
3
|
|
Уметь решать уравнения, неравенства и их системы
|
|
3.1
|
Решать линейные, квадратные уравнения и рациональные
уравнения, сводящиеся к ним, системы двух линейных уравнений и
несложные нелинейные системы
|
|
3.2
|
Решать линейные и квадратные неравенства с одной переменной и
их системы
|
|
3.3
|
Применять графические представления при решении уравнений,
систем, неравенств
|
|
3.4
|
Решать текстовые задачи алгебраическим методом,
интерпретировать полученный результат, проводить отбор решений
исходя из формулировки задачи
|
4.
|
|
Уметь строить и читать графики функций
|
|
4.1
|
Определять значение квадратичной функции по значению аргумента при
различных способах задания функции, решать обратную задачу
|
|
4.2
|
Определять свойства квадратичной функции по её графику (промежутки возрастания, убывания, промежутки знакопостоянства, наибольшее и наименьшее значения)
|
|
4.3
|
Распознавать арифметические и геометрические прогрессии; решать
задачи с применением формулы общего члена и суммы нескольких
первых членов прогрессий
|
5.
|
|
Уметь выполнять действия с геометрическими фигурами,
координатами и векторами
|
|
5.1
|
Решать планиметрические задачи на нахождение геометрических
величин (длин, углов, площадей)
|
|
5.2
|
Распознавать геометрические фигуры на плоскости, различать их
взаимное расположение, изображать геометрические фигуры;
выполнять чертежи по условию задачи
|
|
5.3
|
Определять координаты точки плоскости; проводить операции над
векторами, вычислять длину и координаты вектора, угол между
векторами
|
6.
|
|
Уметь работать со статистической информацией, находить
частоту и вероятность случайного события
|
|
6.1
|
Извлекать статистическую информацию, представленную в
таблицах, на диаграммах, графиках
|
|
6.2
|
Решать комбинаторные задачи путем организованного перебора
возможных вариантов, а также с использованием правила
умножения
|
|
6.3
|
Вычислять средние значения результатов измерений
|
|
6.4
|
Находить частоту события, используя собственные наблюдения и
готовые статистические данные
|
|
6.5
|
Находить вероятности случайных событий в простейших случаях
|
7.
|
|
Уметь использовать приобретенные знания и умения в
практической деятельности и повседневной жизни, уметь
строить и исследовать простейшие математические модели
|
|
7.1
|
Решать несложные практические расчётные задачи; решать задачи,
связанные с отношением, пропорциональностью величин, дробями, процентами; пользоваться оценкой и прикидкой при практических расчётах; интерпретировать результаты решения задач с учётом
ограничений, связанных с реальными свойствами рассматриваемых
объектов
|
|
7.2
|
Пользоваться основными единицами длины, массы, времени,
скорости, площади, объёма; выражать более крупные единицы через
более мелкие и наоборот. Осуществлять практические расчёты по
формулам, составлять несложные формулы, выражающие
зависимости между величинами
|
|
7.3
|
Моделировать реальные ситуации на языке алгебры, составлять
выражения, уравнения и неравенства по условию задачи;
исследовать построенные модели с использованием аппарата
алгебры
|
|
7.4
|
Описывать с помощью функций различные реальные зависимости
между величинами; интерпретировать графики реальных зависи-
мостей
|
|
7.5
|
Описывать реальные ситуации на языке геометрии, исследовать
построенные модели с использованием геометрических понятий и
теорем, решать практические задачи, связанные с нахождением
геометрических величин
|
|
7.6
|
Анализировать реальные числовые данные, представленные в
таблицах, на диаграммах, графиках
|
|
7.7
|
Решать практические задачи, требующие систематического перебора
вариантов; сравнивать шансы наступления случайных событий,
оценивать вероятности случайного события, сопоставлять и
исследовать модели реальной ситуацией с использованием аппарата
вероятности и статистики
|
|
7.8
|
Проводить доказательные рассуждения при решении задач,
оценивать логическую правильность рассуждений, распознавать
ошибочные заключения
|
4. Спецификация контрольных измерительных материалов для проведения диагностической итоговой работы по математике в 9 классе
4.1 Характеристика структуры и содержания работы
Вариант диагностической итоговой работы состоит 10 заданий. По алгебре содержит 7 заданий: в части 1 — 5 заданий; в части 2 — 2 задания. По геометрии - 3 задания: в части 1 — 2 задания; в части 2 — 1 задание.
На выполнение итоговой диагностической работы по математике отводится 90 минут).
Часть 1 направлена на проверку достижения уровня базовой подготовки. Она включает задания 1-7 с решением и ответом. Чертежи из КИМов не переносятся.
Часть 2 включает задания 8-10 и направлена на дифференцированную проверку повышенного уровня владения материалом. В заданиях 8-10 требуется записать решение в развернутом виде и ответ.
4.2 Продолжительность работы
На выполнение диагностической итоговой работы по учебному предмету «Математика» отводится 40 минут.
4.3 Обобщенный план варианта диагностической итоговой работы по математике
Уровни сложности заданий: Б – базовый, П – повышенный
Таблица 3.
№
п/п
|
Основные проверяемые требования к математической подготовке
|
Коды проверяемых элементов содержания
|
Коды разделов элементов требований
|
Уровень сложности
|
Максимальный балл за выполнение задания
|
Часть 1
|
1
|
Уметь выполнять вычисления и преобразования
|
1.5
|
1.1
|
Б
|
1
|
2
|
Уметь выполнять
преобразования алгебраических выражений
|
2.7
|
2.1
|
Б
|
1
|
3
|
Уметь строить и читать графики функций
|
4.1
|
3.3
|
Б
|
1
|
4
|
Осуществлять практические расчеты по формулам, составлять не-
сложные формулы, выражающие зависимости между величинами
|
6.2
|
4.1
|
Б
|
1
|
5
|
Уметь решать уравнения, неравенства и их системы
|
3.1
|
3.1
|
Б
|
1
|
6
|
Уметь выполнять действия с геометрическими фигурами, координа-
тами и векторами
|
9.6
|
5.1
|
Б
|
1
|
7
|
Уметь выполнять действия с геометрическими фигурами, координа-
тами и векторами
|
9.7
|
5.2
|
Б
|
1
|
Часть 2
|
8
|
Уметь решать уравнения, неравенства и их системы
|
3.3
|
3.1
|
П
|
2
|
9
|
Решать текстовые задачи на составление уравнения
|
5.2
|
3.4
|
П
|
2
|
10
|
Уметь выполнять действия с геометрическими фигурами, координа-
тами и векторами
|
9.2
|
5.2
|
П
|
2
|
4.4 Распределение заданий диагностической работы по уровню сложности
Таблица3.
№
|
Уровень сложности
|
Количество
заданий
|
Максимальный первичный балл
|
Процент (%) от максимального первичного балла
|
1
|
Базовый
|
7
|
7
|
54
|
2
|
Повышенный
|
3
|
6
|
46
|
|
Итого
|
10
|
13
|
100
|
4.5. Время выполнения работы
На выполнение диагностической итоговой работы по одному варианту по учебному предмету «Математика» отводится 40 минут
4.6 Дополнительные материалы и оборудование
При проведении работы разрешается использовать линейку, циркуль, карандаш, справочные материалы, содержащие основные формулы курса математики 9 класса, выдаваемые вместе с работой.
4.7 Система оценивания выполнения отдельных заданий и работы в целом
Правильно выполненная работа оценивается 13 баллами.
Правильный ответ на задание 1 – 7 оценивается в 1 балл
Правильный ответ на каждое из заданий 8-10 оценивается 2 баллами.
Таблица 4.
Отметка по пятибалльной шкале
|
«2»
|
«3»
|
«4»
|
«5»
|
Первичные баллы
|
0-5
|
6-7
|
8-10
|
12-13
|
4.8 Рекомендации по подготовке к итоговой диагностической работе
Специальная подготовка к проверочной работе не требуется.
Варианты
контрольных измерительных материалов для проведения
диагностической итоговой работы по математике в 9 классе
Вариант 1
Часть 1
1. Вычислите 2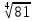 + +  + + 
2. Сократите дробь  . .
3. На рисунке изображен график функции 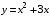 . Используя график, решите неравенство . Используя график, решите неравенство  . .

4. В арифметической прогрессии 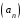  , ,  . Найдите . Найдите  . .
5. Решите уравнение
6 . Найдите ∠KОM, если известно, что градусная мера дуги MN равна 124°, а градусная мера дуги KN равна 180°. Точка O — центр окружности. . Найдите ∠KОM, если известно, что градусная мера дуги MN равна 124°, а градусная мера дуги KN равна 180°. Точка O — центр окружности.
7. Две стороны треугольника 13 см и 48 см, а угол между ними - 600. Найдите площадь треугольника.
Часть 2

8.
9. Расстояние между городами А и В равно 490 км. Из города А в город В со скоростью 55 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города В выехал со скоростью 90 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся?
10. Площадь прямоугольного треугольника, катеты которого равны, составляет 32 дм2. Найдите радиус окружности, описанной около этого треугольника.
Вариант 2
Часть 1
1. Вычислите 5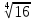 + + 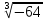 + + 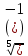
2. Выполните сложение дробей  . .
3. На рисунке изображен график функции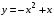 . Используя график, решите неравенство . Используя график, решите неравенство  . .
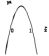 
4. Найдите 11 член арифметической прогрессии: 3; – 2; – 7;….
5. Решите уравнение
6. Найдите ∠DEF, если градусные меры дуг DE и EF равны150° и 68° соответственно.
7. Две стороны параллелограмма 9 см и 56 см, а угол между ними - 300. Найдите площадь параллелограмма.
Часть 2
8 . .
9. Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Одновременно с ним из В в А выехал велосипедист. Велосипедист ехал со скоростью, на 11 км/ч большей скорости пешехода, и сделал в пути получасовую остановку. Найдите скорость пешехода, если известно, что они встретились в 8 км от пункта В.
10. Площадь прямоугольного треугольника, один катет которого в 3 раза больше другого составляет 24 м2. Найдите радиус окружности, описанной около этого треугольника.
Ответы
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
Вариант 1
|
2
|

|
[-3; 0]
|
-0,2
|
-2
|
560
|
158,5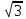 см2 см2
|
(-2;1);
(-2;-1)
|
220 км
|
4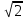 дм дм
|
Вариант 2
|
5
|
х+5
|
(∞;0)
|
-47
|
1
|
710
|
252 см2
|
(1;1);
(-1;1)
|
5км/ч
|
2 м м
|
|
 Скачать 129.73 Kb.
Скачать 129.73 Kb.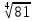 +
+  +
+ 
 .
. 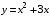 . Используя график, решите неравенство
. Используя график, решите неравенство  .
. 
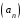
 ,
,  . Найдите
. Найдите  .
.
 . Найдите ∠KОM, если известно, что градусная мера дуги MN равна 124°, а градусная мера дуги KN равна 180°. Точка O — центр окружности.
. Найдите ∠KОM, если известно, что градусная мера дуги MN равна 124°, а градусная мера дуги KN равна 180°. Точка O — центр окружности.
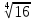 +
+ 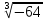 +
+ 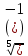
 .
.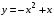 . Используя график, решите неравенство
. Используя график, решите неравенство  .
.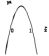


 .
. 

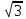 см2
см2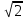 дм
дм
 м
м