Зачет по геометрии. Тема: «Подобие треугольников».
Ф.И._____________________________________________________Класс___________1 вариант.Часть 1.Определить являются ли ниже приведенные утверждения верными (да -+, нет-)
№
|
Утверждение
|
+/-
|
1
|
Любые два прямоугольных треугольника подобны
|
|
2
|
Если два угла одного треугольника соответственно пропорциональны двум углам другого треугольника, то такие треугольники подобны.
|
|
3
|
Два треугольника называются подобными, если их углы соответственно равны
|
|
4
|
Если два треугольника подобны, то их соответствующие стороны равны
|
|
5
|
Отношение периметров двух подобных треугольников равно коэффициенту подобия
|
|
6
|
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны.
|
|
7
|
Любые два прямоугольных и равнобедренных треугольника подобны.
|
|
8
|
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны
|
|
9
|
Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника, то такие треугольники подобны
|
|
10
|
Любые два равнобедренных треугольника подобны.
|
|
11
|
Высота прямоугольного треугольника равна среднему геометрическому между проекциями катетов на гипотенузу
|
|
12
|
Диагонали трапеции при пересечении образуют четыре подобных треугольника.
|
|
Часть 2.Необходимо ответить на вопросы и записать формулировку геометрического утверждения
№
|
Вопрос
|
Ответ
|
1
|
Что такое средняя линия треугольника?
|
|
2
|
Дать определение проекции катета на гипотенузу?
|
|
3.
|
Какие треугольники называются подобными?
|
|
4.
|
Сформулируйте признаки подобия треугольников:
|
1.
2.
3.
|
5
|
Запишите теорему об отношении площадей подобных треугольников.
|
|
6
|
Сформулируйте утверждение о пропорциональных отрезках в прямоугольном треугольнике.
|
|
Часть 3. (выполнить любое из предложенных заданий)1).
Доказать любой признак подобия треугольников2). Доказать, что высота прямоугольного треугольника, проведенная из вершины прямого угла есть среднее геометрическое между проекциями катетов на гипотенузу.
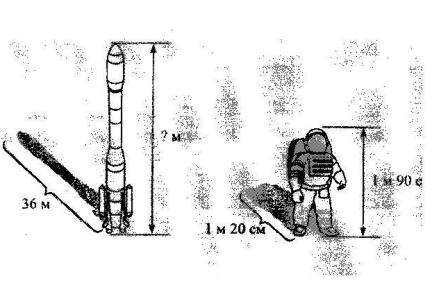
3). Решить задачу: Найдите высоту ракеты, по данным рисунка
Зачет по геометрии. Тема: «Подобие треугольников».
Ф.И._____________________________________________________Класс___________2 вариант.  Скачать 61.03 Kb.
Скачать 61.03 Kb.
