Полупроводниковые диоды. Полупроводниковый диод

• Название: Полупроводниковый диод
• Анкор: Полупроводниковые диоды.docx
• Дата: 09.02.2018
• Размер: 1.64 Mb.
• Имя файла: Полупроводниковые диоды.docx
• Тип: Документы; #15375
• страница: 12 из 15

5.6. Разряд конденсатора на цепь с резистором и катушкой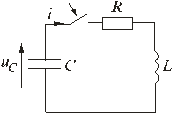

Рис. 5.13

Пусть в цепи, изображенной на рис. 5.13, конденсатор был заряжен до напряжения u_C(0_-) = U₀. Исследуем процессы в контуре, образованном резистором, конденсатором и катушкой после замыкания в момент t = 0 ключа. Так как источники в цепи отсутствуют, то установившиеся составляющие решений равны нулю. Решение будет состоять из одной свободной составляющей.

5.6.1. Составление характеристического уравнения. Определение собственных частот цепи

По второму закону Кирхгофа t ≥ 0 имеем:

.

Учитывая, что , получаем дифференциальное уравнение второго порядка для свободной составляющей напряжения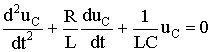

.

Характеристическое уравнение при этом имеет вид:

.

Характер электромагнитных процессов в контуре зависит от соотношения параметров R, L, С, входящих в выражение для корней характеристического уравнения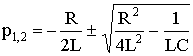

.

В зависимости от знака подкоренного выражения корни могут быть вещественными или комплексно-сопряженными. Они определяют характер свободных составляющих переходных токов и напряжений.

5.6.2. Апериодический разряд конденсатора на катушку и резистор

Рассмотрим процесс разряда конденсатора на резистор R и катушку L. Если параметры контура из резистора, катушки и конденсатора удовлетворяют условию или , то корни характеристического уравнения контура вещественные, различные, т.е. р₁ ≠ р₂, и отрицательные. В этом случае напряжение на конденсаторе описывается уравнением

u_C = u_Cсв = A₁ · e^p₁^t + A₂ · e^p₂^t,

где А₁ и А₂ – постоянные интегрирования, определяемые из начальных, условий.

Свободный ток равен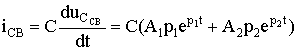

.

Установившиеся составляющие напряжения на конденсаторе и тока равны нулю. Поэтому их переходные значения равны свободным составляющим:

u_C = u_Cсв; i = i_св.

Определим из начальных условий постоянные интегрирования А₁ и А₂. При t = 0, u_C(0) = U₀ и i(0) = 0. Подставив их в выражения для переходных напряжений и токов при t = 0 имеем

U₀ = A₁ + A₂; 0 = A₁ p₁ + A₂ p₂.

Отсюда

A₁ = U₀ p₂ / (p₂ - p₁); A₂ = -U₀ p₁ / (p₂ - p₁);

С учетом начальных условий запишем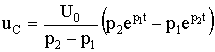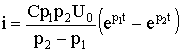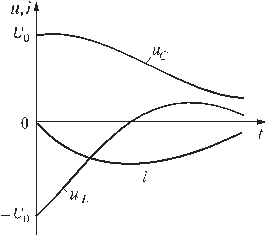

; .


Рис. 5.14

Произведение корней по теореме Виета: p₁ p₂ = 1 / (LC), следовательно, ток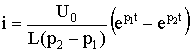

.

Напряжение на катушке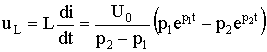

.

Графики зависимости тока и напряжения от времени, показанные на рис. 5.14 позволяют говорить об апериодическом разряде конденсатора. Апериодическим называется такой разряд, при котором конденсатор все время разряжается, т.е. функция u_C(t) - убывающая, а ток i не меняет своего направления, в нашем случае он отрицателен. Сделаем некоторые выводы.

1. 
   Апериодический разряд конденсатора в цепи R, L, С возникает при вещественных, отрицательных и неравных корнях характеристического уравнения.
   
2. 
   При апериодическом разряде напряжение на конденсаторе уменьшается от начального значения до нуля, а ток сначала возрастает по модулю, затем уменьшается, проходя через максимальное значение.
   
3. 
   Напряжение на катушке уменьшается от начального значения, проходит через нулевое значение, изменяя знак и, достигнув наибольшего значения, уменьшается до нуля.
   

5.6.3. Предельный апериодический разряд конденсатора на катушку и резистор

При соотношении параметров контура из конденсатора, катушки и резистора

,

где R_КР - критическое сопротивление резистора R, корни характеристического уравнения контура вещественные, равные и отрицательные:

p₁ = p₂ = p = -R / (2L).

Переходный процесс получается апериодическим, но граничным с колебательным процессом. Переходный ток и переходное напряжение в этом случае имеют вид:

u_C = (A₁ + A₂ t) e^pt;

.

При начальных условиях u_C(0) = U₀; i(0) = 0 находим: А₁ = U₀; A₂ = -p U₀. С учетом найденных постоянных интегрирования получаем решения:

u_C = U₀ (1 - pt) e^pt;
;
.

Зависимости i, u_C, u_L такие же, как для апериодического разряда.

5.6.4. Периодический (колебательный) разряд конденсатора на цепь с резистором и катушкой

При соотношении параметров контура из конденсатора, катушки и резистора , где R_КР – критическое сопротивление цепи, корни характеристического уравнения комплексные сопряженные:

p_1,2 = -α ± jω,

где α = R / (2L) – коэффициент затухания свободной составляющей;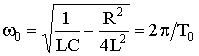
– угловая частота собственных колебаний контура;
Т₀ – период собственных колебаний.

Поскольку , то можно ввести обозначения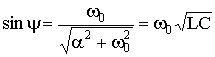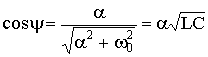

, , .

Свободная составляющая переходного напряжения при комплексно-сопряженных корнях (см. п.п. 5.2.1)

u_Cсв = A e^-αt sin(ω₀t + ψ),

Для свободной составляющей тока имеем

i_св = C A e^-αt (-α sin(ω₀t + ψ) + ω₀ cos(ω₀t + ψ)).

С учетом начальных условий при t = 0, u_C = U₀ , i = 0 из последних двух уравнений находим константы интегрирования:

U₀ = A sin ψ; 0 = C A (-α sin ψ + ω₀ cos ψ).

и далее

.

Запишем переходные напряжения и ток:

u_C = U_Cm e^-αt sin(ω₀t + ψ);
i = -I_m e^-αt sin(ω₀t + π);
u_L= U_Lm e^-αt sin(ω₀t - ψ),

где ; .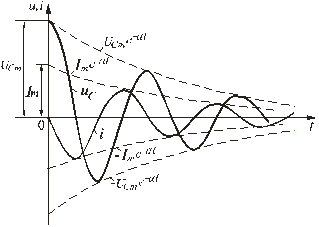


Рис. 5.15

Зависимости переходных напряжения и тока u_C, i показаны на рис. 5.15. Они представляют собой затухающие синусоиды. Скорость затухания колебаний оценивают декрементом колебаний. Декремент колебания - это постоянная, зависящая от параметров R, L, С и равная отношению амплитуд переходных параметров, отстающих друг от друга на период колебания Т₀, например: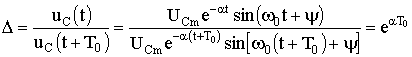

.

Часто пользуются логарифмическим декрементом колебания: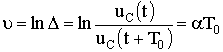

.

В предельном случае чисто консервативной системы (R = 0) Δ = 1 колебания в параллельно соединенных конденсаторе и катушке носят незатухающий характер. Период этих колебаний дается формулой Томпсона , а частота незатухающих колебаний .