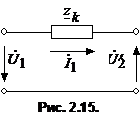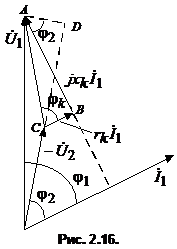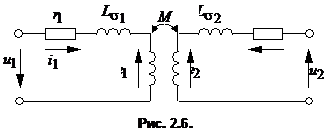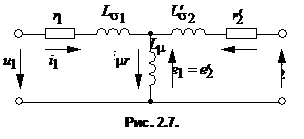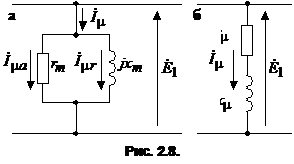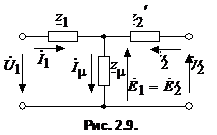Полупроводниковые диоды. Полупроводниковый диод
 Скачать 1.64 Mb. Скачать 1.64 Mb.
|
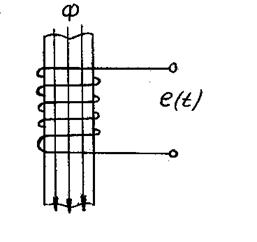
5.7. Включение контура из конденсатора, резистора, катушки на постоянное напряжение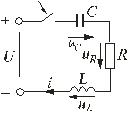 Рис. 5.16 Рассмотрим электромагнитные процессы, возникающие после замыкания ключа в цепи, изображенной на рис. 5.16 в предположении, что конденсатор был предварительно не заряжен, т.е. uC(0-) = 0. Характеристическое уравнение и вид его корней будут такими же, как и в цепи, рассмотренной в п. 5.6. 5.7.1. Апериодический процессМежду разрядом конденсатора на резистор с катушкой и включением на постоянное напряжение контура (см. рис. 5.16) существует аналогия. Так же, как при разряде конденсатора, установившаяся составляющая тока равна нулю. Установившееся напряжение на конденсаторе uCу = U. Следовательно, начальное значение свободной составляющей напряжения на конденсаторе 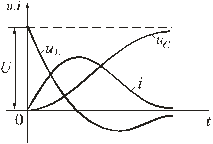 Рис. 5.17 uCсв(0+) = uC(0+) - uCу(0-) равно uCсв(0+) = -U. То есть знаки постоянных интегрирования А1 и А2 в отличие от рассмотренного в п. 5.6 случая изменяются на противоположные. В этом случае переходное напряжение на конденсаторе, ток и напряжение на катушке определяются по формулам: 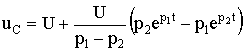 ; ;; 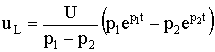 . .Кривые uC(t), uL(t) и i(t) приведены на рис. 5.17. 5.7.2. Колебательный процессВключение рассматриваемого контура на постоянное напряжение может сопровождаться колебательным переходным процессом. При этом в отличие от процесса разряда конденсатора (см. п. 5.6) знак начального значения преходящего напряжения, следовательно, и коэффициента А, изменится на противоположный. Переходные напряжения и ток приобретут вид: 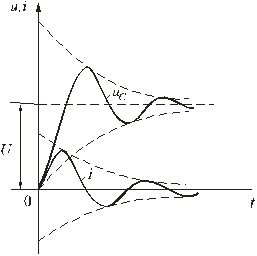 Рис. 5.18 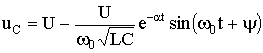 ; ;; 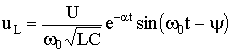 . .Кривые uC(t) и i(t) показаны на рис. 5.18. Кривая тока отображает затухающие колебания относительно нулевого значения, а напряжения на конденсаторе – относительно установившегося значения. Следует отметить, что за время переходного процесса контура часть энергии источника переходит в тепло, а другая часть запасается в электрическом поле конденсатора в виде: 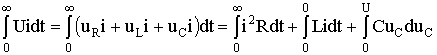 т.е. 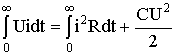 . .55.Магнитные цепи постоянных и переменных магнитных потоков. Ферромагнитные материалы и их характеристики. В реальных цепях переменного тока помимо обычных элементов - сопротивлений, индуктивностей и ёмкостей часто встречаются и элементы с ферромагнитными сердечниками - катушки с сердечниками. Особенность цепей переменного тока с ферромагнитными элементами заключается в том, что переменные токи в обмотках и магнитные потоки в сердечниках взаимосвязаны. С одной стороны, магнитные потоки зависят от токов в обмотках, и при анализе цепей приходится в значительной мере пользоваться методами, разработанными для магнитных цепей с постоянными магнитными потоками. С другой стороны, токи в обмотках зависят от характера изменения магнитных потоков, и это весьма усложняет исследования. Учитывая эти особенности, на практике вводят различные допущения и упрощения. Например, иногда считают связь между индукцией и напряженностью магнитного поля линейной, но учитывают потери энергии в сердечниках. Иногда - наоборот, пренебрегают потерями в сердечниках, но связь между индукцией и напряженностью считают нелинейной. В цепях с ферромагнитными элементами нельзя считать индуктивность и взаимную индуктивность постоянными, и приходится использовать непосредственную зависимость между ЭДС и магнитным потоком или потокосцеплением. В основе индукционного действия магнитного поля лежит закон электромагнитной индукции (закон Фарадея-Максвелла). Согласно этому закону в контуре, движущемся в неизменном поле так, что его стороны пересекают магнитные линии, или в контуре, помещенном в изменяющееся во времени магнитное поле, индуктируется ЭДС, численно равная скорости изменения во времени магнитного потока, пронизывающего этот контур:
Когда контур состоит из W витков, пронизываемых одним и тем же потоком, индуктированная в нем ЭДС равна: Часто различные группы витков (W1, W2,...) одной и той же катушки пронизываются различными потоками Ф1, Ф2, ...; в этом случае полная ЭДС катушки равна сумме ЭДС отдельных групп витков: 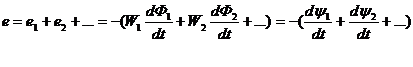 здесь Сумму магнитных потоков, сцепленных с каждым из витков, называют магнитным потокосцеплением. Произведения W Ф являются потокосцеплениями соответствующих групп витков. Уравнение, определяющее величину ЭДС как скорость изменения потокосцепления замкнутого контура представляет собой математическую формулировку закона электромагнитной индукции в наиболее общем виде. Знак "-" в нем определяется выбором условно положительных направлений индуктированной ЭДС и потока, пронизывающего контур.
При возрастании магнитного потока ( Общее выражение для индуктированной ЭДС справедливо и для цепей со взаимной индуктивностью. Пусть Ф2 - полный магнитный поток 2-й катушки, а ФM2 - его часть, пронизывающая 1-ю катушку. Тогда потокосцепление 1-й катушки будет равно но оно относится и к току i : получаем формулу для взаимной индуктивности: ЭДС, наведенную магнитным полем 2-й катушки в 1-й катушке, теперь удобно определить по формуле: Пусть витки катушки пронизывает синусоидально изменяющийся магнитный поток: тогда, если пренебречь рассеянием поля, ЭДС, наведенная в витках катушки, определится выражением: где Это выражение часто используется на практике при расчетах различных машин переменного тока. Заметим, что ЭДС отстает по фазе от магнитного потока на угол 90 . В цепях, содержащих катушки с ферромагнитными сердечниками, возникают из-за их нелинейности несиносоидальные токи и напряжения. Часто для упрощения анализа их заменяют эквивалентными синусоидальными величинами. Амплитуда эквивалентной синусоидальной величины определяется произведением действующего значения несиносоидальной величины на 2, а фазовый сдвиг между эквивалентными синусоидами напряжения и тока определяются из соотношения: где параметры P, U и I относятся к несинусоидальным величинам. Переход к эквивалентным синусоидам позволяет вести анализ цепей символическим методом, а также строить векторные диаграммы на комплексной плоскости. Переменный магнитный поток замыкается по внешнему контуру магнитной цепи, поэтому цепь постоянного тока не нужно защищать от действия больших переменных ЭДС, которые наводились этим потоком в обмотке с числом витков в вышеуказанном примере. В данном случае и ток, и магнитный поток несинусоидальны. В силу симметрии ВбАХ сердечника четные гармоники тока в обмотках должны были бы иметь разные знаки, но это невозможно, поскольку эти обмотки соединены последовательно и в них протекает один и тот же ток. Поэтому переменный ток содержит только нечетные гармоники. 56.Применение закона полного тока для анализа магнитных цепей Обмотка имеет W витков и обтекается током I. Магнитные линии внутри кольца представляют собой концентрические окружности с центров точке О. Применим к контуру Cх, совпадающему с одной из магнитных линий, проходящих в магнитопроводе, закон полного тока. При этом будем считать:
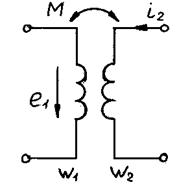
Тогда Отсюда [А/м], где Lx – длина контура, вдоль которого велось интегрирование; rx – радиус окружности. Вектор внутри кольца зависит от расстояния rх. Если α – ширина кольца << d, то эта разница между значениями Н в пределах сердечника не велика. При этом в расчет допустимо принять для всего поперечного сечения магнитопровода одно значение напряженности магнитного поля: Hср = IW / L 57.Устройство и принцип действия однофазного трансформатора Принцип действия трансформатора Действие трансформатора заключается в следующем. При прохождении тока в первичной катушке / ею создается магнитное поле, силовые линии которого пронизывают не только создавшую их катушку, но частично и вторичную катушку //. Примерная картина распределения силовых линий, создаваемых первичною катушкою, изображена на рис. 1б. Как видно из рисунка, все силовые линии замыкаются вокруг проводников катушки /, но часть их на рис. 1б силовые линии 1, 2, 3, 4 замыкаются также вокруг проводников катушки //. Таким образом катушка // является магнитно связанной с катушкою / при посредстве магнитных силовых линий. Степень магнитной связи катушек / и //, при коаксиальном расположении их, зависит от расстояния между ними: чем дальше катушки друг от друга, тем меньше магнитная связь между ними, ибо тем меньше силовых линий катушки / сцепляется с катушкою //. Так как через катушку / проходит, как мы предполагаем, переменный ток, т. е. ток, меняющийся во времени по какому-то закону, например по закону синуса, то и магнитное поле, им создаваемое, также будет меняться во времени по тому же закону. Например, когда ток в катушке / проходит через наибольшее значение, то и магнитный поток, им создаваемый, также проходит через наибольшее значение; когда ток в катушке / проходит через нуль, меняя свое направление, то и магнитный поток проходит через нуль, также меняя свое направление. В результате изменения тока в катушке / обе катушки / и // пронизываются магнитным потоком, непрерывно меняющим свою величину и свое направление. Согласно основному закону электромагнитной индукции при всяком изменении пронизывающего катушку магнитного потока в катушке индуктируется переменная электродвижущая сила. В нашем случае в катушке / индуктируется электродвижущая сила самоиндукции, а в катушке // индуктируется электродвижущая сила взаимоиндукции. Если концы катушки // соединить с цепью приемников электрической энергии (см. рис. 1а), то в этой цепи появится ток; следовательно приемники получат электрическую энергию. В то же время к катушке / от генератора направится энергия, почти равная энергии, отдаваемой в цепь катушкой //. Таким образом электрическая энергия от одной катушки будет передаваться в цепь второй катушки, совершенно не связанной с первой катушкой гальванически (металлически). Средством передачи энергии в этом случае является только переменный магнитный поток. Изображенный на рис. 1а трансформатор весьма несовершенен, ибо между первичной катушкой / и вторичной катушкой // магнитная связь невелика. Магнитная связь двух обмоток, вообще говоря, оценивается отношением магнитного потока, сцепляющегося с обеими обмотками, к потоку, создаваемому одной катушкой. Из рис. 1б видно, что только часть силовых линий катушки / замыкается вокруг катушки //. Другая часть силовых линий (на рис. 1б — линии 6, 7, 8) замыкается только вокруг катушки /. Эти силовые линии в передаче электрической энергии от первой катушки ко второй совершенно не участвуют, они образуют так называемое поле рассеяния. Работа однофазного трансформатора под нагрузкою При холостой работе трансформатора магнитный поток создается током первичной обмотки или, вернее, магнитодвижущей силой первичной обмотки. Так как магнитная цепь трансформатора выполняется из железа и потому имеет небольшое магнитное сопротивление, а число витков первичной обмотки берется обычно большим, то ток холостой работы трансформатора невелик, он составляет 5—10% нормального. Если замкнуть вторичную обмотку на какое-либо сопротивление, то с появлением тока во вторичной обмотке появится и магнитодвижущая сила этой обмотки. 58.Уравнения электрического и магнитного состояния трансформатора Представим трансформатор в упрощенном виде. Пренебрежем потоками рассеяния и активным сопротивлением обмоток: Фs1= 0; Фs2= 0; R1= 0; R2= 0. Такой трансформатор называется идеальным трансформатором. Для идеального трансформатора по второму закону Кирхгофа можно записать уравнения электрического состояния обмоток: ; Согласно закону электромагнитной индукции можно записать: где - потокосцепление, = Li. Возьмем отношение: 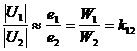 Это уравнение отражает важнейшее свойство идеализированного трансформатора преобразовывать напряжение без искажения формы. Так как на W1 подается переменное напряжение, то Выразим "е" через "Ф": 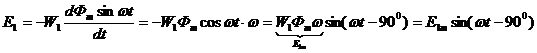 так как Получили амплитудное значение ЭДС: Найдем действующее значение ЭДС: По аналогии для вторичной обмотки: Эти уравнения для идеализированного трансформатора используются при анализе электрических процессов в трансформаторе. Теперь учтем наличие потоков рассеяния Фs1 и Фs2 и активное сопротивление обмоток R1 и R2. Запишем с учетом этих величин уравнение по второму закону Кирхгофа для первичной и вторичной обмоток трансформа- тора: Параметр представляет собой падение напряжения на индуктивности и в комплексной форме записывается как j X1I1. Перейдем к комплексным значениям параметров: U1= -E1+ j X1I1+ R1I1= -E1+I1(R1+ j X1) = -E1+I1Z1 Получили уравнение электрического состояния первичной обмотки трансформатора в комплексной форме. Для вторичной обмотки 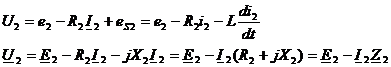 Получили уравнение электрического состояния для вторичной обмотки трансформатора. Трансформатор - электромагнитное устройство. Для него справедлив закон полного тока: где Н - напряженность магнитного поля, lср - длина средней магнитной линии сердечника. Рассмотрим 2 режима работы: холостой ход и режим номинальной нагрузки. Для холостого хода: Для номинальной нагрузки: Правые части уравнений неизменны, поэтому приравниваем между собой левые части: Поделим каждый член наW1 и частично преобразуем , где I10 - ток холостого хода или намагничивающий ток, Знак " - " в уравнении отражает размагничивающее действие тока I2. Таким образом, ток первичной обмотки можно представить как сумму двух токов: приведенный ток вторичной обмотки I2| плюс намагничивающий ток I10. Еслт сердечник идеален, то I10= 0 и 0 =I1W1+I2W2 Таким образом, трансформация тока осуществляется без искажения формы: 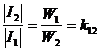 59.Векторная диаграмма трансформатора в нагрузочном режиме. Схема замещения трансформатора Векторные диаграммы при нагрузке строят по уравнениям (16). Вид векторной диаграммы зависит от характера нагрузки (рис. 14).
Векторная диаграмма а рис. 14 соответствует активно-индуктивной нагрузке, а векторная диаграмма б - активно-емкостной нагрузке. Сопоставляя обе диаграммы, можно заключить, что при и увеличение активно-индуктивной нагрузки вызывает снижение напряжения , а при увеличении активно-емкостной нагрузки напряжение возрастает. Это объясняется тем, что при активно-индуктивной нагрузке происходит некоторое размагничивание трансформатора (поток Ф уменьшается, так как ток имеет составляющую, направленную навстречу току ), а при активно-емкостной нагрузке трансформатор дополнительно намагничивается (поток Ф возрастает, так как ток имеет составляющую, совпадающую с ).
Для оценки диапазона изменения напряжения вводится величина , представляющая собой арифметическую разность между вторичным напряжением трансформатора при холостом ходе () и при номинальной нагрузке (). Напряжение первичной обмотки принимается постоянным и равным номинальному . 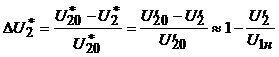 . (18) . (18)Для расчета примем допущение , тогда, используя упрощенную схему замещения (рис.15), получим Уравнению (19) соответствует векторная диаграмма, представленная на рис. 16. Из векторной диаграммы следует, что
Подставляя приближенное выражение для в уравнение (18), получим Отрезок можно выразить через составляющие напряжения короткого замыкания:
где . Учитывая, что На рис. 17 представлена зависимость Максимальное снижение напряжения имеет место при , а при напряжение не зависит от нагрузки. С этой целью вторичную обмотку трансформатора необходимо привести к первичной по числу витков. Формально приведение осуществляется путем умножения второго уравнения системы (8) на коэффициент трансформации :
где - приведенное значение напряжения вторичной обмотки. Из условия равенства мощностей приведенной и неприведенной обмоток получаем выражение для приведенного тока: . (11) С учетом этого выражения уравнение (10) приобретает вид где Реактивная составляющая намагничивающего тока приведенного трансформатора определяется суммой токов, . Если теперь уравнения приведенного трансформатора записать в виде
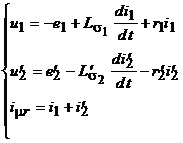 (13) (13)и учесть, что , то электромагнитную связь в схеме (рис. 6) можно заменить электрической (рис. 7). Схема замещения трансформатора (рис. 7) является его расчетной схемой при анализе как установившихся, так и переходных процессов. При синусоидальных напряжениях и токах для описания установившихся режимов вместо дифференциальных уравнений удобнее пользоваться комплексными уравнениями для действующих значений токов и напряжений. Чтобы получить комплексные уравнения трансформатора, нужно заменить на : 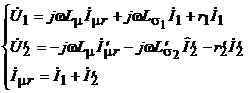 (14) (14)Введем обозначения: - индуктивное сопротивление взаимной индукции; - индуктивное сопротивление рассеяния первичной обмотки; - индуктивное сопротивление рассеяния вторичной обмотки; - комплексное сопротивление первичной обмотки; - комплексное сопротивление вторичной обмотки. Уравнения в новых обозначениях имеют вид 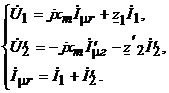 (15) (15)При выводе уравнений трансформатора предполагалось, что процесс намагничивания сердечника не связан с потерями энергии на гистерезис и вихревые токи. Их можно учесть приближенно, приняв допущение, что потери в стали пропорциональны следующим величинам: отсюда ясно, что потери в стали можно учесть, если параллельно сопротивлению включить активное сопротивление 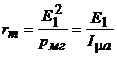 (рис. 8, а). При расчетах удобно параллельные ветви свернуть в одну ветвь (рис. 8, б) с активным сопротивлением: (рис. 8, а). При расчетах удобно параллельные ветви свернуть в одну ветвь (рис. 8, б) с активным сопротивлением:
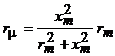 и индуктивным сопротивлением 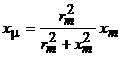 . .Тогда уравнения трансформатора с учетом потерь в стали примут вид
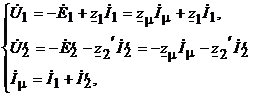 , (16) , (16)где . Уравнениям (16) соответствует Т-образная схема замещения приведенного трансформатора, представленная на рис. 9. Численные расчеты по уравнениям (16) и соответствующей им схеме замещения (рис. 9) обычно выполняют в относительных единицах. В качестве базисных принимаются - действующее значение номинального фазного напряжения первичной обмотки; - действующее значение номинального фазного тока первичной обмотки; 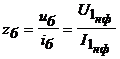 - фазное сопротивление номинальной нагрузки. - фазное сопротивление номинальной нагрузки.Переход к относительным единицам осуществляется путем деления величин в именованных единицах на соответствующие базисные значения. Сопротивления трансформатора в относительных единицах имеют следующий порядок: ; Необходимо отметить, что сопротивления и не являются постоянными. Они зависят от насыщения магнитопровода. Остальные сопротивления можно считать практически постоянными для всех режимов работы трансформатора. 60.Паспортные данные трансформаторов. Определение параметров схемы замещения трансформатора по опытам холостого хода и короткого замыкания 61.Устройство и применение трехфазных трансформаторов. Фазный и линейный коэффициенты трансформации. Энергию трехфазного переменного тока можно преобразовать тремя однофазными трансформаторами, соединенными в трансформаторную группу (групповой трехфазный трансформатор), или одним трехфазным трансформатором. Групповой трехфазный трансформатор представляет собой три однофазных трансформатора (рис.1.11.). Однако относительная громоздкость, большой вес и повышенная стоимость – существенные недостатки группового трехфазного трансформатора, поэтому в авиационном оборудовании нашли применение только трехфазные трансформаторы. Трехфазный трехстержневой трансформатор(рис.1.12.) имеет три стержня, на которых расположены три первичных и три вторичных обмотки. У трехстержневого трансформатора меньше размеры и масса по сравнению с групповым. Недостатком трехстержневого трансформатора является то, что магнитное сопротивление для м.д.с. крайних фаз больше, чем для средней фазы, поэтому намагничивающие токи образуют несимметричную систему. При холостом ходе, несмотря на симметричное питающее напряжение, токи в фазах не будут одинаковыми: в крайних фазах они будут больше, чем в средней фазе. За ток холостого хода в трехфазном трансформаторе следует принимать среднее арифметическое значение токов трех фаз. Однако несимметрия токов холостого хода не имеет большого значения, так как даже при незначительной нагрузке она сглаживается. 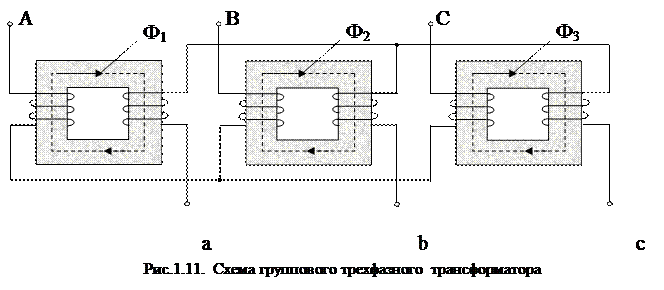 Выводы обмоток трансформатора принято обозначать буквами: · первичной обмотки: начала – А, В, С; концы - X,Y,Z; · вторичной обмотки: начала – а, b, с; концы – x, y, z. 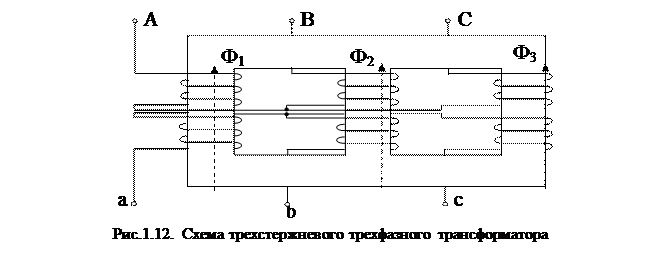 Схемы и группы соединения трехфазных трансформаторов Первичную и вторичную обмотки трехфазного трансформатора соединяют в звезду, треугольник или зигзаг (рис.1.13.). Примечание:Соединение в зигзаг применяют только в трансформаторах специального назначения, например, в трансформаторах для выпрямительных устройств. 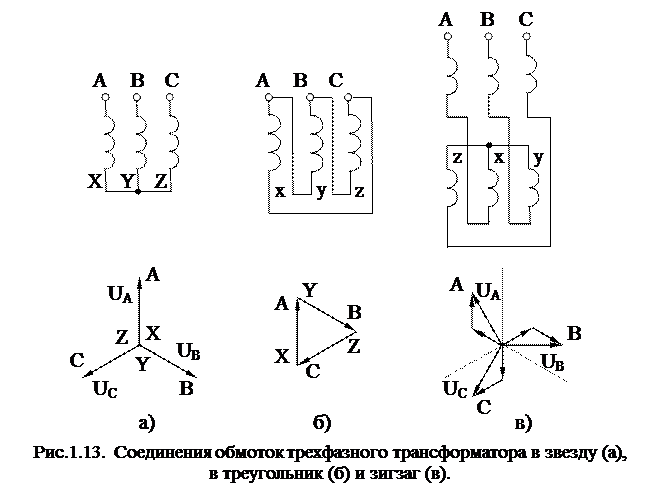 Соединение обмотки в звезду обозначается значком Υ.Соединение в треугольник обозначается соответственно значкомΔ. Соединение в зигзаг – значком Z. При соединении в зигзаг обмотка, как правило, делится на две одинаковые части, расположенные на соседних стержнях. Это способствует уменьшению асимметрии напряжений при несимметричной нагрузке фаз. При соединении звездой линейное напряжение больше фазного: , а при соединении обмоток треугольником линейное напряжение равно фазному: UЛ=UФ. Следовательно, отношение линейных напряжений в трехфазном трансформаторе зависит не только от соотношения чисел витков фазных обмоток, но и от схемы соединения обмоток. Так, например, при соединении обмоток Υ/Υ или Δ/Δ отношение линейных напряжений обмоток равно , при соединении 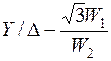 , а при соединении обмоток , а при соединении обмоток 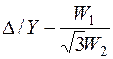 . .Первичную и вторичную обмотки трехфазного трансформатора можно соединять в различные схемы: Y/Y; Y/Δ; Δ/Y и Δ/Δ. В числителе указывается схема соединения первичной обмотки, а в знаменателе – вторичной. Если при соединении звездой выводится нулевая точка, то применяется знак Yо. Примечание:В авиационных трансформаторах, как правило, первичная обмотка является обмоткой высшего напряжения ВН, а вторичная – обмоткой низшего напряжения НН). Способы соединения первичной и вторичной обмоток, порядок соединения обмоток при образовании звезды и треугольника, соответствующая маркировка начала и концов фаз приводят к различной разности фаз соответствующих линейных напряжений первичной и вторичной обмоток. Эта разность фаз имеет большое практическое значение, особенно при параллельной работе. Так как возможный угол разности фаз всегда кратен 30 градусам, то принято различать 12 групп соединений (в пределах 3600). Для определения номера группы используют циферблат часов. Вектор первичной линейной э.д.с. направляют на цифру 12 циферблата, а номер группы определяется часом, на который попадает при этом вектор соответствующей вторичной линейной э.д.с. Примечание: Совпадение по фазе векторов первичной и вторичной Э.Д.С., эквивалентное совпадению стрелок часов на циферблате, обозначается группой 0, а не 12. На рис.1.14 показано, что при соединении первичной и вторичной обмоток по схеме Y/Y можно получить группы 6 и 0. Приведенное на рис.1.15. соединение по схеме Υ/Δ дает группы 11 и 5.
 Стандартизированы две группы соединения обмоток трехфазных трансформаторов: 0 и 11: 1) звезда – звезда с выведенной нулевой точкой ; 2) звезда – треугольник ; 3) звезда с выведенной нулевой точкой – треугольник ; 4) звезда - зигзаг с выведенной нулевой точкой (Y/ -11); 5) треугольник - звезда с выведенной нулевой точкой (Δ/ΥО -11). На самолетах при выполнении трехпроводной сети обычно применяются трехфазные трансформаторы группы .
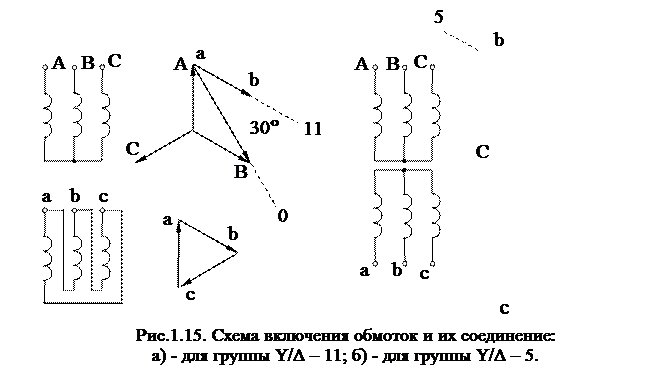 Трехфазные же трансформаторы характеризуются коэффициентами трансформации: а) фазным – отношением числа витков wвн фазы обмотки высшего напряжения (ВН) к числу витков wнн фазы обмотки низшего напряжения (НН), б) линейным – отношением линейного напряжения обмотки ВН к линейному напряжению обмотки НН в режиме холостого хода , 62.Вращающееся магнитное поле. |