Ответы на вопросы, математика печать. Понятие функции, способы задания функций. Область определения. Четные и нечетные, ограниченные, монотонные функции. Примеры
 Скачать 183.88 Kb. Скачать 183.88 Kb.
|
Постоянной величиной наз-ся величина,сохраняющая одно и то же значение (число «пи»). Если вел-на сохр.пост-е зн-е лишь в усл-ях данного процесса,то в этом сл-е она наз-ся параметром. Переменной наз-ся вел-на,кот.может принимать различные числ.зн-я. Понятие функции. Опр: Если каждому эл-ту Х множества Х(х принадл. Х) ставится в соотв-е вполне опред-ный эл-т у множества Y (y принадл. Y),то говорят, что на мн-ве Х задана функция y=f(x). При этом х наз-ся независимой пер-й (аргументом),y-зависимой пер-й, а буква f обозн-т закон соответствия. Мн-во Х наз-ся областью определения ф-ции, а мн-во Y – обл.зн-й ф-ции. Под обл-ю опред-я ф-ции подразумевается обл.допустимых зн-й независ.переменной х, т.е. мн-во таких зн-й х,при кот.ф-ция y=f(x) вообще имеет смысл. Способы здания фун-й. а)аналитический с.- если ф-ция задана ф-лой вида y=f(x). Одна ф-ция может иметь (допустим)2 аналитических выражения. б)Табличный – состоит в том,что ф-ция задаётся таблицей, содержащей зн-я аргумента х и соотв.зн-я ф-ции f(x). в)Графический – состоит в изображении графика ф-ции – мн-ва точек (х;у) плоскости, абциссы которых есть зн-я аргумента х, а ординаты – соотв-е им зн-я ф-ции y=f(x). г)Словесный – если ф-ция описывается правилом её составления,напр.ф-ция Дирифле:f(x)=1, если х-рационально; f(x)=0, если х – иррационально. Чётность и нечётность. f(-x)=f(x) – чётная, график симметричен относит. Оу. (х2) f(-x)=-f(x) – нечётная, гр.симметричен относит. Начала координат. (х3) В противном сл-е ф-ция y=f(x) наз-ся ф-цией общего вида. Монотонность. Ф-ция y=f(x) возрастает на промеж.Х, если большему зн-ю аргумента соотв. большее зн-е ф-ции. Ф-ция y=f(x) убывает на промеж.Х, если большему зн-ю аргумента соотв. меньшее зн-е ф-ции. Ф-ции возрастающие или убыв-е наз-ся монотонными ф-циями. Ограниченность. Ф-ция f(x) – ограниченная на промеж.Х, если сущ-ет такое полож.ч-ло M>0, что |f(x)|<и равно М для любого х принадлежащего промежутку Х. Например, ф-ция y=sinx ограничена на всей числ-й оси,т.к. |sinx|<и равно1 для любого х, принадл-го R. Периодичность. Ф-ция периодическая с периодом T не=0, если для любых из обл.опред-я ф-ции f(x+T)=f(x). Напр., ф-ция у=sinx имеет период T=2«пи»,т.к. для любых х sin(x+2«пи»)=sinх. 2. Понятие элементарной функции. Основные элементарные функции и их графики (постоянная, степенная, показательная, логарифмическая). Элементарная ф-ция. Опр: Эл.ф-ция - составленная из основных элементарных (константа,степенная,логарифм. и т..д.) при помощи алгебраических действий или при помощи конечного числа операций образования сложной ф-ции. Алгебраической наз-ся ф-ция, в кот. над аргументом производится конеч.ч-ло алгебраич.действий. К ч-лу алг.ф.относят: 1)целая рациональная ф-ция: у=а0хn + а1хn-1 + … + аn-1х + аn; 2)дробно-рациональная ф-ция – отношение 2-х многочленов; 3)иррациональная ф-ция – если в составе операций над аргументом имеется извлечение корня. Преобр-е графиков. 1.Гр.ф-ции у=f(х+а) есть гр. у=f(х), сдвинутый (при а>0 влево, при а<0 вправо) на |а| ед-ц парал-но оси Ох. 2.Гр.ф-ции у=f(х)+b есть гр. у=f(х), сдвинутый (при b>0 вверх, при b<0 вниз) на |b| ед-ц параллельно оси Оу. 3.Гр.ф-ции у=mf(х) (m не=0) есть гр. у=f(х), растянутый (при m>1) в m раз или сжатый (при 0 4.Гр.ф-ции у=f(kх) (k не=0) есть гр. у=f(х), сжатый (при k>1) в k раз или растянутый (при 0 Осн.эл.ф.:(только непериодические ф-ци!) 1)Степенная ф: а) y=xn (n принадл.N) Обл.опр.: (-б,+б); Обл.зн.:(-б,+б),если n-неч.,[0;б), если n-неч.; Чет/нечет: Неч,если n-неч; чет-если n – чёт.; График: Возрастает на (-б;+б), если n- неч; убывает на (-б;0], возр.на (0;б), если n – чёт. б) у= x-n (n принад. N). Обл.опр.: (-б;0) U (0,б); Обл.зн.: (-б,0) U (0,б), если n – неч., [0,б), если n – чёт. Чет/нечет: Неч.,если n –неч., Чёт,если n-чёт.; График: Убыв.на (-б,0) и на (0,б),если n-неч.; возр.на (-б,0) и убыв. на (0,б),если n-чёт. в) у =nкв.к.х (n принад. N, n>1). Обл.опр.: (-б,б), если n-неч., [0,б), если n-чёт. Обл.зн.: (-б,б),если n-неч., [0,б), если n-чёт. Чёт/нечёт: Неч., если n-неч, общ. в., если n-чёт. График: Возр. на (-б,б), если n-неч, возр. На [0,б), если n-чёт. 2)Показательная ф.: у=аx (а>0, а не=1) Обл.опр.: (-б,б); Обл.зн.: (0,б); Чёт/нечёт: общ.в; График: Возр. на (-б,б), если а>1, убыв. на (-б,б), если (-б,б), если 0<а<1. 3)Логарифмическая ф.: у=logax (a>0, a не=0) Обл.опр.: (0,б); Обл.зн.: (-б,б); Чёт/Нечёт: общ.в; График: Возр. на (0,б), если а>1, убыв. на (0,б), если 0<а<1. 3.Предел последовательности при n-→∞ и предел функции при x→∞. Признаки существования предела (с доказательством теоремы о пределе промежуточной функции) Если каждому натуральному числу nЄN поставлено в соответствии вполне определенное число an , то говорят, что на множестве натуральных чисел задана числовая посл-ть { an }. Числ. посл-ть - это функция натурального аргумента Пример an= 2n+1/ 3n+2 a1 = 2*1+1/3*1+2=3/5 Качественное опр-е: Предел числ посл-ти – это число к которому стремится общий член посл-ти (n-→∞) | an -A|→0 Количественное опр-е:A называется пределом числ. посл-ти an , если для любого даже сколь угодно мало положительного числа эпсилон, найдется такой номер N, зависящиеся от E, что для всех n будет выполняться нер-во {A= lim an } <=> { 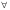 E>0 N=N/E:n>N→| an -A| E>0 N=N/E:n>N→| an -A|Геометрический смысл предела числ. посл-ти Нер-во | an -A| Границы (A-E; A +E) означают, что практически большинство членов посл-ти находящихся в E – окрестности в т.А, а вне этой окр-ти находится ограниченное число членов посл-ти, находится вне этой окр-ти 1;1/2;1/3; ….1/10……1/11;1/12 вне Е окр-ти принадлежат Е-окр. Предел функции в бесконечности A= lim f(x) Число А называется пределом функции при x→∞ ., если для любого даже сколь угодно малого полож числа E>0 , найдется такое полож число S>0 (зависящее от Е, S=S (E)), что для всех х таких что |х|>S верно нер-во |х|>S |f(x)-A| Признаки существования предела Теорема1. Если числовая последовательность{ an } монотонна и ограниченна, то она имеет предел. Теорема2.Если в некоторой окрестности точки х0 функция заключена между двумя функциями φ(х) и ψ(х), имеющими одинаковый предел А при x→х0 (x→∞.), то функция имеет тот же предел А. Пусть при x→х0 lim φ(х)=А, lim ψ (х)=А Это означает, что для любого Е>0 найдется такое число σ>0, что для всех х≠ х0 и удовлетворяющих условию |х- х0|< σ Будут верны одновременно нер-ва |φ(х)-А|<Е, | ψ (х)-А|<Е если А-Е< φ(х) <А+Е, А-Е< ψ (х) <А+Е Т.к. по условию функция заключена между 2-мя функциями, т.е. φ(х) То из нер-в следует, что А-Е< f(x) <А+Е, т.е. |f(x)-A| А это и означает, что lim f(x)=А 4. Определение предела функции в точке. Основные теоремы о пределах (одну из них доказать) Определение 1. ЧислоAназываетсяпределом функцииy=f(x)в точкеx=x0, если значения функцииf(x) приближаются (стремятся) к числуA, когда значения аргументаx приближаются (стремятся) к числуx0(xx0). Обозначения: Определение 1'. ЧислоAназываетсяпределом функцииy=f(x)в точкеx=x0, если для любого как угодно малого числа>0 существует такое число>0, выбираемое в зависимости от, что для всех значений аргументаx, удовлетворяющих неравенствуx-x0<, соответствующее значение функции удовлетворяет неравенствуf(x)-A<. Заметим, что не всякая функция имеет предел в заданной точке. При нахождении предела функции используется два основных способа:
Теорема 1. Если функцияy=f(x) имеет предел в точкеx=x0, то только один. Теорема 2. Пусть Теорема 3. Пусть 1. 2. 3. 5. Бесконечно малые величины (определение). Свойства бесконечно малых (одно из них доказать). Бесконечно большие величины, их связь с бесконечно малыми. Функция y=f(x) называется БМ при определенном стремлении аргумента, если рано или поздно ее значение по модулю будут меньше любого наперед выбранного полож числа Е, т.е. |f(x)| lim f(x)=0 Св-ва БМ величин 1.алгебраическая сумма конечного числа БМ величин есть величина БМ 2.произведение БМ величины на ограниченную функцию есть величина БМ 3.частное от деления БМ величины на функцию, предел который отличен от нуля, есть величины БМ. Доказательство 1 св-ва. Дано α(х,), β(х) – БМ Д-ть: (α(х,)+ β(х)) – БМ при x→х0 Док-во по усл. α(х,) есть БМ при x→х0 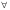 Е>0 Е>0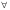 Е’= Е/2>0, Е’= Е/2>0, 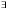 σ1>0, х≠ х0 σ1>0, х≠ х0|х- х0|< σ1 (1) | α(х,) |<Е/2 (2) По усл β(х) – БМ при x→х0  Е’= Е/2>0, Е’= Е/2>0,  σ2>0, х≠ х0 σ2>0, х≠ х0|х- х0|< σ2 (3) | β (х,) |<Е/2 (4) σ= min (σ1 ;σ2) |х- х0|< σ (5) Тогда значения х удовл (5) будут верны оба нер-ва (2) и (4) складываем их и получаем | α(х,)+ | β (х,) <Е/2+Е/2 |x+y|<|x|+|y| По свойству модулей получим |α(х,)+ β(х) |<Е (6) Итак, для любого Е>0 существует такое число σ>0, что для всех х≠ х0 удовл. усл.(5) будет верно нер-во (6) Функция y=f(x) называется ББ при определенном стремлении аргумента, если рано или поздно ее значение по модулю будут больше любого наперед выбранного полож числа | f(x) |>M. M>0 lim f(x)= ∞ Теорема о связи между БМ и ББ величинами 1.Если функция имеет при x→х0 (x→∞.), предел, равный числу А, то эту функцию можно представить в виде суммы, этого числа А и БМ α(х,) при x→х0 (x→∞.), f(x) = A+ α(х,) 2.Если функцию можно представить как сумму числа А и БМ α(х,) при x→х0 (x→∞.), то число А – есть предел этой функции. lim f(x)=A 6. Второй замечательный предел, число е. Понятие о натуральных логарифмах. Второй замеч.предел. Рассматривается числовая послед. {an} an=(1+1/n)n. Данная послед-ть монотонно возрастает и ограничена. а1=2, а2=2,25, а3≈2,37…, а4≈2,44…, а100≈2,71, а1000≈2,71, а10000≈2,71. limn→∞(1+1/n)n≈2,71 (Эйлерово число). Опр:Числом е (2-м замечат.пред-м)наз-ся предел числовой последовательности e=limn→∞(1+1/х)х. Опред.числа е через предел ф-ции: (e=limх→∞(1+1/х)х. (e=limх→0(1+x)1/х. (e=limх→х0(∞)(1+α)1/α, limх→х0(∞)α=0. logex=lnx – натуральный логарифм.(логарифм по основанию е) Обознач. ln:logex=lnx. дт(0+0)=-∞ дт(+∞)=∞ дту=1 н=дтчб уЮ0 7. Непрерывность функции в точке и на промежутке. Свойства функций. Непрерывных на отрезке. Точки разрыва. Примеры. Функция f(x) называется непрерывной в т.x0 , если она удовлетворяет след 3 условиям: 1. определена в т. x0. 2. имеет конечный предел функции при x→х0 3. этот предел равен значению функции f(x0) в т. x0 т.е. lim f(x)= f(x) Непрерывность функции на отрезке Функция y=f(x) непрерывна на [a.b], если непрерывна в каждой точки этого отрезка Свойства функции y=f(x) непрерывна на [a.b] 1. Если функция y=f(x) непрерывна на [a.b],то она ограниченна на этом отрезке. 2. Если функция y=f(x) непрерывна на [a.b],то она достигает своего max или min значения. 3. Если функция y=f(x) непрерывна на [a.b],и значения ее на концах отрезка f(a)иf(b) имеют противоположные знаки, то существует такая т. С Є[a.b], что функция f(c) = 0 Точка х0 называется точкой разрыва функции y=f(x), если эта функция в данной точке не является непрерывной Пример. Y=1/x f(0) – не сущ. 8. Производная и ее геометрический смысл. Уравнение касательной к плоской кривой в заданной точке. Опр:Производной ф-ции у=f(x) наз-ся предел отнош.приращ.ф-ции к приращ.аргумента, при усл-ии, что приращ.арг. мало, а предел сущ-ет и конечен. y’=lim∆x→0∆y/∆x. АВ – секущая гр.ф-ции y=f(x) α=└ВАС. Kсек=tgα=tg└ВАС=ВС/АС=∆у/∆х Если ∆х→0, то т.В→с т.А. Секущая АВ→в своё предельное положение, называемой касательной АВ. Значит Kкас= lim∆x→0∆y/∆x. Т.о. Геом.смысл производной заключ.в том, что производная в т.касания равна угл.коэф-ту касательной, т.е. f’(x)=Kкас. Ур-е касат-й: y-y0=f’(x0)(x-x0). y0=f(x0) 9. Дифференцируемость функций одной переменной. Связь между дифференцируемостью и непрерывностью функции (доказать теорему). Нахождение производной функции называется дифференцированием этой функции. Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке. Функция дифференцируемая во всех точках промежутка х, называется дифференцируемой на этом промежутке. |

 Понятие функции, способы задания функций. Область определения.
Понятие функции, способы задания функций. Область определения.