Ответы на вопросы, математика печать. Понятие функции, способы задания функций. Область определения. Четные и нечетные, ограниченные, монотонные функции. Примеры

• Название: Понятие функции, способы задания функций. Область определения. Четные и нечетные, ограниченные, монотонные функции. Примеры
• Дата: 14.06.2018
• Размер: 183.88 Kb.
• Имя файла: Ответы на вопросы, математика печать.docx
• Тип: Документы; #46948
• страница: 3 из 3

20. Дифференциал функции и его геометрический смысл. Инвариантность формы дифференциала 1-го порядка.
Опр. Дифференциалом фун-и наз-ся главная, линейная относительно дельта х часть приращения фун-и, равная произведению производной на приращение независимой переменной.

Геометр.смысл диф-ла. Диф-л фун-и есть приращение ординаты касательной, проведенной к графику фун-и y=f(x) в данной точке, когда х получает приращение дельта х.

Dy=f’(u) du – это сво-во диф-ла получило название инвариантности формы диф-ла.
21. Понятие первообразной функции. Неопределенный интеграл и его свойства (одно из свойств доказать).
Функция F(x) называется первообразной функцией для функции f(x) на промежутке х, если на всех точках этого промежутка, выполняется равенство:

F’(x)=f(x)

Совокупность всех первообразных F(x)+C для функции y=f(x) называется неопределенным интегралом от функции y=f(x)

⌠f(x)dx=F(x) +C

Свойства неопределенного интеграла

1. 
   (f(x)dx)’=f(x)
   

Док-во

(⌠f(x)dx)’=(F(x)+C)’=F’(x)+C’=f(x)

2. 
   d(⌠f(x)dx)’=f(x)dx дифференциал от неопределенного интеграла равен подынтегральному выр-ю
   
3. 
   ⌠dF=F+C интеграл от диф-ла функции равен самой функции с точностью до константа
   
4. 
   ⌠са(ч)вч=с⌠а(ч)вч
   
5. 
   ⌠(а(ч)+-п(ч))вч= ⌠а(ч)вч+-⌠п(ч)вч
   

22. Метод замены переменной в неопределенном интеграле и особенности применения этого метода при вычислении определенного интеграла.
Метод замены переменной в неопределенном интеграле - ∫ f(x) dx = ∫ f(φ(t)) φ’ (t) dt;

Метод замены пер-ой в опр.интеграле - ^b∫_a f(x) dx = ^b∫_a f(φ(t)) φ’ dt.
23. Метод интегрирования по частям для случаев неопределенного и определенного интегралов (вывести формулу). Примеры.
Неопределенный интеграл

Рассмотрим дифференцируемые функции переменной

U=U(x) и V=V(x)

Т.к. d(uv) = (uv)’dx=u’vdx+uv’dx= du*v+u*dv, то проинтегрируем по переменной х это равенство и учтем, что интеграл суммы функции – это сумма интегралов

⌠d(uv)= ⌠vdu+⌠udv

uv=⌠vdu+⌠udv

Метод интегрирования по частям применяется, когда нельзя вычесть интеграл методом замены переменной.

Пример.

⌠lnx*x⁸dx = {u=lnx;dv= x⁸dx; du = 1/8dx; v= ⌠ x⁸dx= x⁹/9}=lnx* x⁹/9-⌠ x⁹/9-1/xdv=lnx* x⁹/9-1/9⌠ x⁸dx=lnx* x⁹/9-1/9* x⁹/9+C

Определенный интеграл.

^b⌠udv=(uv-⌠vdu)^b│

^{a a}
u=u(x), v=v(x)

^b⌠udv=uv^b│-⌠ ^b vdu

^{a a a}
24. Определенный интеграл как предел интегральной суммы. Свойства определенного интеграла.
Опр. Пусть предел интегральной суммы при стремлении max дельта х_i к нулю существует, конечен и не зависит от способа выбора точек. Тогда этот предел называется определенным интегралом от функции y=f(x) на [a,b], обозначается ^b∫_a f(x) dx, а сама фун-я y=f(x) наз-ся интегрируемой на отрезке [a,b].

Сво-ва опр.интеграла:

1. Постоянный множитель можно выносить за знак интеграла.

2. Интеграл от алгебраической суммы двух фун-ий равен такой же сумме интегралов от этих фун-ий.

3. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей.

4. Обе части неравенства можно почленно интегрировать.

5. Теорема о среднем. Если фун-я y=f(x) непрерывна на отрезке [a,b], (где ab∫_a f(x) dx = f(ξ)(b-a).
25. Теорема о производной определенного интеграла по переменному верхнему пределу. Формула Ньютона–Лейбница.
Теорема. Производная интеграла от непрерывной функции по переменному верхнему пределу равна подынтегральной функции при значении верхнего предела.

Φ(x)= ^x⌠f(x)dx = ^x⌠f(t)dt

^{a a}
Φ’(x ) =f(x)

Док-во Φ’(x )=lim ∆φ/∆x= lim φ(x+∆x)- φ(x)/ ∆x= lim ^x+∆x ∫_а f(t)dt-^x⌠_а f(t)dt/ ∆x = lim ^x⌠ f(t)dt+



+ ^x+∆x ⌠f(t)dt- ^x⌠ f(t)dt/∆x = lim (x+∆x-x)*f(ξ)/ ∆x = lim f(ξ)= f(x)

^{a a}

Т.о. Φ(x)- это первообразная для f(x). Две первообразные для одной функции отличаются на константу..

^x⌠ f(t)dt = F(x)+C

^a

Формула Ньютона-Лейбница.

Определенный интеграл в пределах от a и b от непрерывной функции равен приращению любой ее первообразной на отрезке [a;b].

^b⌠f(x)dx = F(b)-F(a)

^a

1.при x=a ^a⌠f(t)dt=F(a)+C

^a

F(a)+C→C= -F(a)

2.x=b

^b⌠f(t)dt=F(b)-F(a)

^a
26. Несобственные интегралы с бесконечными пределами интегрирования. Интеграл Пуассона (без доказательства).
Опр. Несобственным интегралом ^+∞∫_а f(x) dx от фун-и f(x) на полуинтервале [a;+∞] наз-ся предел фун-и Ф(t) при t, стремящимся к +∞.
^+∞∫_-∞ e^-x2/2 dx – несобственный интеграл Эйлера-Пуассона.
27. Вычисление площадей плоских фигур с помощью определенного интеграла. Примеры.
Пусть фун-я y=f(x) неотрицательна и непрерывна на отрезке [a,b]. Тогда по геометрич.смыслу определ.интеграла площадь S под кривой y=f(x) на [a,b] численно равна опред.интегралу, т.е. S = ^b∫_a f(x)dx. 2. Пусть фун-я y=f(x) неположительна и непрерывна на [a,b]. Тогда S = ^b∫_a (-f(x)) dx, т.е. S = - ^b∫_a f(x)dx. 3. Пусть на отрезке задана непрерывная фун-я общего вида. Тогда, S=S₁+S₂+S₃, т.е. равна алгебраич.сумме соответствующих опред.интегралов: S = ^c∫_a f(x)dx - ^d∫_c f(x)dx + ^b∫_d f(x)dx. 4. Тео-ма. Пусть на отрезке заданы непрерывные фун-и y=f₁(x) и y=f₂(x) такие, что f₂(x)> f₁(x). Тогда площадь S фигуры, заключенной между кривыми y=f₂(x) и y=f₁(x), на отрезке вычисляется по формуле: S = ^b∫_a (f₂(x) – f₁(x)) dx.

При-р: Найти пло-дь фиг-ры, огранич.линиями y=x²-2, y=x.(рис.11.18).

Реш-е: система: y=x²-2 и y=x => (-1;-1) и (2;2). На отр-ке [-1,2] x>x²-2. f₂(x)=x, f₁(x)=x²-2. S=²∫_-1 (x-(x²-2)) dx = x²/2 ²|_-1 – x³/3 ²|_-1 +2x ²|_-1 =1/2(4-(-1)²) – 1/3(2³-(-1)³) +2(2-(-1)) = 4,5 (ед.²).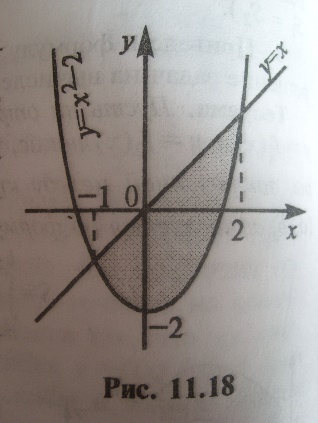




28. Понятие о дифференциальном уравнении. Общее и частное решения. Задача Коши. Задача о построении математической модели демографического процесса.
Опр. Дифференциальным уравнением называется уравнение, связывающие искомую функцию одной или нескольких переменный, эти переменные и производные различных порядков данной фун-и.

Общим решением диф-ного урав-я n-ого порядка называется такое решение: y=φ (x, C₁, ..., C_n), которое является фун-ей переменной x и n произвольных независимых постоянных C₁, C₂,…, C_n.

Частным решением диф-ного урав-я наз-ся решение, получаемое из общего решения при некоторых конкретных числовых значениях постоянных C₁, C₂,…, C_n.

Задачи Коши – это решения урав-я удовлетворяющих условию x₀ y₀ : y₀=f(x₀).

29. Простейшие дифференциальные уравнения 1-го порядка (разрешенные относительно производной, с разделяющимися переменными) и их решение. Примеры.
Рассмотрим вопросы теории диф-ных урав-й на примере урав-й первого порядка, разрешенных относительно производной, т.е. таких, кот.допускают представление в виде y’=f(x,y). Тео-ма. Пусть в диф-ном урав-и фун-я f(x,y) и ее частная производная дf/дy непрерывны на открытом множестве Г координатной плоскости Oxy. Тогда: 1)Для всякой точки (x₀,y₀) множества Г найдется реш-е y=y(x) урав-я, удовл-щее условию y₀=y(x₀); 2) Если два решения y=y₁(x) и y=y₂(x) урав-я совпадают хотя бы для одного значения x=x₀, т.е. если y₁(x₀)=y₂(x₀), то эти решения совпадают для всех тех значений переменной х, для которых они определены. Прим-рЖ нэ=ню Реш-еЖ а(чбн) = нб да.дн=1ю н=Су^чю Пусть н=н(ч)ж н₀=н(ч₀)ж С=н₀у^-ч0ж н=н(ч) и н=Су^ч=н₀у^-ч0у^ч=н₀у^ч-ч0 – уравнения совпадают при ч=ч₀ю.
30. Однородные и линейные дифференциальные уравнения 1-го порядка и их решения. Примеры.
Дифференциальное урав-е первого порядка наз-ся однородным, если оно может быть представлено в виде y’=g(y/x). Понятие однород-го диф-го урав-я связано с однород-ми фун-ми. Фун-я y=f(x,y) наз-ся однородной степени k (по переменным x и y), если для произвольного числа α выполняется равенство f(αx, αy)=α^k f(x,y) При-р: f(x,y)=x² – xy. f(αx, αy)=(αx)² – (αx)(αy)=α²(x² – xy)= α² f(x,y), данная фун-я однород-я степени 2.

Диф-ное урав-е первого порядка наз-ся линейным, если оно имеет вид y’+f(x)y=g(x). В случае, когда фун-я g(x) тождественно равна нулю, урав-е наз-ся однород-м, в противном случае – неоднород-м.




31. Определение числового ряда. Сходимость числового ряда. Свойства сходящихся рядов. Примеры.
32. Необходимый признак сходимости рядов (доказать). Гармонический ряд и его расходимость.
^n→∞,

Числовым рядом называется бесконечная последовательность чисел, соединенных знаком сложения.

u₁+u₂+….u_n= ∑ u_n=S сумма сходящегося ряда

Предел частной суммы Sn ряда (конечный или бесконечный) называется суммой ряда S=lim Sn

Пример

1. 
   1-+1-1+1-1+1….
   

S₁=1; S₂=0; S3=1

Пределы частной суммы не сущ – ряд рас-ся

Сходимость числового ряда

Ряд называется сходящимся, если существует конечный предел последовательности, его частичных сумм, если конечного предела не сущ при n→∞, то ряд называется рас-ся

Необходимый признак сходимости.

Тео-а. Если числовой ряд сх-ся, то предел его общего члена Un при n→∞,равен 0

lim Un=0

^n→∞,

lim U_n=lim (Sn-S_n-1)= limSn-lim S_n-1= S-S=0

^n→∞,

След-е. Если lim Un≠0 то ряд рас-ся

При-ы. Исследуем сходимость ряда.
∑4n+5/3n+7

ⁿ⁼¹

lim 4n+5/3n+7= lim 4n/3n≠0 рас-ся


33. Признаки сравнения для знакоположительных рядов. Примеры.

Числовым рядом называется символ

а₁ + а₂ + а₃ + … + а_n,

где а₁, а₂, а₃,…, a_n – элементы некоторой числовой последовательности. Иначе говоря, ряд есть сумма бесконечного числа слагаемых. Число a_n называется n-м членом ряда.

Сумма S_n = a₁ + a₂ +…+a_n называется n-й частной суммой ряда. Рассмотрим последовательность S_n, сост

,

авленную из частных сумм некоторого ряда: S₁, S₂, … S_n… Если

то данный ряд называется сходящимся, а число S =  - суммой ряда. Если последовательность, составленная из частных сумм ряда не имеет предела, то ряд называется расходящимся . Таким образом, сумма бесконечного числа слагаемых не всегда имеет смысл.

Примеры:

1. 
   Сумма бесконечного числа членов геометрической прогрессии с : 1 +q² +…+ qⁿ + … Существует сумма ряда . Поэтому такой ряд является сходящимся.
   
2. 
   Ряд сходится.
   
3. 
   Ряд (гармонический) расходится.
   

Знакоположительные ряды. Признаки сравнения. Ряд называется знакоположительным, если для всех n а_n  0.

1-й признак сравнения: пусть даны два знакоположительных ряда и, причем все члены первого ряда меньше соответствующих членов второго ряда:. Тогда а) если рядсходится, то и рядсходится; б) если рядрасходится, то и рядрасходится.

Доказательство: а) известно, что знакоположительный ряд сходится:. Заметим, чтоB_n монотонно возрастающая последовательность, имеющая предел, следовательно, она ограничена сверху. Поэтому В_n  B (В – точная верхняя граница). Но . Следовательно, последовательность монотонно возрастающая последовательность A_n также ограничена сверху и имеет предел, следовательно ряд сходится, ч. т. д.; б) имеем расходящийся ряд. Допустим, что рядсходится. Тогда меньший рядтакже сходится (см. пункт а) данной теоремы), а это не так. Мы пришли к противоречию. Следовательно, ряд.

Замечание: 1-й признак сравнения остается в силе, если неравенство a_n  b_n верно не для всех n, а для n  n₀. Это вытекает из свойств сходимости.

2-й признак сходимости: пусть даны два знакоположительных ряда ии пусть существует= С 0 (С > 0, т.к. предел отношения двух положительных последовательностей также положителен). Тогда оба ряда сходятся или расходятся одновременно.

Доказательство: по условию , это означает, чтоили - <  - C < ; С -  <  < C + ;

(C - ) b_n < a_n < (C + ) b_n. *)

Поскольку  - любое число, мы можем взять 0 <  < C, тогда С -  > 0. Допустим, что ряд сходится. Тогда, по 1-му признаку сравнения, рядтакже сходится, следовательно (по тому же признаку) сходится и ряд(неравенство выполняется, начиная с некоторого номера). Аналогично (через правую часть двойного неравенства *) доказывается эта теорема для двух расходящихся рядов.

34. Признак Даламбера сходимости знакоположительных рядов. Пример.
Пусть даны 2 полож. ряда: (1) a₁+a₂+a₃+a_n ; (2) b₁+b₂+b₃+b_n

Причем члены (1) ряда не превосходят членов (2) ряда .

Тогда, если рас-ся ряд (1), то и рас-ся ряд (2)

Если сх-я ряд (2) то и ряд (1)– сх-ся

Если a_n и b_n – эквивалентные величины, т.е. k≠0 и k≠∞ то ряд (1) и (2) ведут себя одинаково, т.е. сх-ся или рас-ся одновременно

Признак Даламбера

Рассмотрим полож. ряд (1) a₁+a₂+a₃+a_n

Пусть существует предел

lim a_n+1/a_n = q

_n→∞,

Тогда, если q>1 то ряд рас-ся

q<1 то ряд сх-ся

q=1 то установить сх-ть по признаку невозможно
ВОПРОС 33 И 34 НУЖНО ОБЪЕДИНИТЬ, ИЛИ СДЕЛАТЬ КОРОЧЕ 33.
35. Знакочередующиеся ряды. Признак Лейбница сходимости знакочередующихся рядов. Пример.

36. Знакопеременные ряды. Абсолютная и условная сходимость рядов. Пример.

Под знакочередующимся рядом понимается ряд, в котором члены попеременно то положительны, то отрицательны.

Признак Лейбница

Ряд a₁-a₂+a₃-a₄+a_n a_n>0

Ряд сх-ся , если выполнены 2 усл

1. 
   члены ряда монотонно убывают по абсолютной величине., т.е
   

a_n≥a_n+1

2. 
   lim a_n=0
   

^n→∞

Пример . исследовать сх-ть ряда

1-½²+⅓² +(-1)^n-1/n²

Т.к. члены убывают по абс величине 1>½²>⅓² и предел общего члена lim 1/n²=0 по признаку ряд сх-ся.

Абсолютно и условно сходящиеся ряды

Ряд называется абсолютно сходящимся, если сх-ся как сам данный ряд, так и ряд составленный из абсолютных величин его членов.

Ряд называется условно сходящимся, если сам данный ряд сх-ся, а ряд, составленный из абсолютных величин его членов рас-ся.

Св-ва абсолютно и условно сходящихся рядов существенно отличаются, так абс. Сходящиеся ряды напоминают конечные суммы, их можно складывать, умножать и т.д., а вот условно сходящиеся ряды этими св-вами не обладают.

1-1/2+1/3-1/4…. Условно сх-ся.