Ответы на вопросы, математика печать. Понятие функции, способы задания функций. Область определения. Четные и нечетные, ограниченные, монотонные функции. Примеры
 Скачать 183.88 Kb. Скачать 183.88 Kb.
|
|
Связь между дифференцируемостью и непрерывностью функции. Если функция y=f(x) дифференцируема в т.х0 , то она непрерывна в этой точке. Док-во. Согласно определению производной y’= lim ∆y/∆x ∆x→0 согласно теореме о связи предела с БМ величинами y’= ∆y/∆x + α׀ *∆x ∆xy’=∆y+∆x+α(∆x) если ∆x→0. то и ∆y →0.т.е. непрерывна Непрерывна в т. х0 функция y’=f(x) не обязательно дифференцируема в этой точке. 10. Основные правила дифференцирования функций одной переменной (одно из этих правил доказать). Осн.правила диф-ния ф-ции одной переменной: 1.Производная постоянной равна нулю,т.е. с’=0. 2.Произв.арг-та равна 1,т.к. х’=1. 3.Произв-я алгебрач.суммы конечного ч-ла дифференцируемых ф-ций равна такой же сумме производных этих ф-ций, т.е. (u+ν)’=u’+ ν’. 4.Произв.произведений 2-х дифференц-х ф-ций (uν)’=u’ν+uν’. Следствие1:Пост.множ-ль можно выносить за знак производной: (cu)’=cu’. Следствие2: (uvw)’=u’vw+uv’w+uvw’ Доказательство: Пусть u=u(x) и ν=ν(x) – дифференцируемые ф-ции. Найдём производную ф-ции y=uν. 1º.Дадим аргументу х приращение ∆х≠0. Тогда ф-ции u и ν получат наращенные зн-я u+∆u и ν+∆ν, а ф-ция y – значение y+∆y=(u+∆u)(ν+∆ν). 2º.Найдём приращ.ф-ции ∆y=(u+∆u)(ν+∆ν)-uν = uν + ∆uν + u∆ν + ∆u∆ν-uν = ∆uν + u∆ν + ∆u∆ν. 3º.Составим отношение ∆y/∆x, кот.представим в виде ∆y/∆x=(∆y/∆x)ν + u(∆ν/∆x) + (∆u/∆x)(∆ν/∆x)∆x. 4º.Найдём предел этого отнош-я при ∆х→0, используя теоремы о пределах lim∆x→0∆y/∆x= lim∆x→0(∆u/∆x)ν + u lim∆x→0(∆ν/∆x) + lim∆x→0(∆u/∆x)∙lim∆x→0(∆ν/∆x)∙lim∆x→0∆x. На основании опр-я производной получили,что y’=u’ν+uν’+u’ν’∙0 или y’=u’ν+uν’.чтд. 5.Производная частного двух дифференцируемых ф-ций м.б.найдена по ф-ле: (u/ν)’=(u’ν-uν’)/ν2. (ν≠0). 11.Формулы производных основных элементарных функций (одну из формул вывести). Производная сложной функций. Формулы производных основных элементарных функции. 1. С’ = 0 2. x’=1 3. (u+v)’=u’+v’ 4. (uv)’=u’v+uv’ 5. (cu)’= cu’ 6. (u/v)’= u’v-uv’/v2 7. (un)’= nun-1*u’ 8. (√г)э=(1.2√г)*гэ 9. (1.г) =-1.г2*гэ 10. (уг)э= уг*гэ 11. (au)’= au lna*u’ 12. (lnu)’=1/u*u’ 13. (logau)’ = (1/ulna)*u’ Выводим формулу y=lnx
x. ∆x≠0 y+∆y=ln(x+∆x) 2.Находим приращение функции∆y=f(x+∆x)-f(x) ∆y=ln(x+∆x)-lnx=ln(x+∆x/x)= ln (1+∆x/x) 3.Cоставляем отношение ∆y/∆x ∆y/∆x= 1/∆x*ln (1+∆x/x) 4.Находим предел этого отношения при ∆x→0 т.е. y’=lim∆y/∆x (если этот предел существует). y’= lim∆y/∆x= lim 1/∆xln(1+∆x/x)= (0/0)= lim ln(1+y)/xy=1/xlimln(1+y)1/y= 1/xlimlne=1/x Производная сложной функции Пусть y=f(u) и u=φ(x) – дифференцируемые функции от своих аргументов, тогда производная сложной функции y=f (φ(x) существует и равна производной данной функции но промежуточному аргументу и умноженной на производную самого промежуточного аргумента по независимой переменной х, т.е. y’=f’(u)’*ux’ y’=lim ∆y/∆x= lim ∆y*∆u/∆x*∆u= lim ∆y/∆u*lim∆u/∆x= lim ∆y/∆u= f’(u)*u’ (если∆x→0, то и ∆u→0, т.к. u= φ(x)- непрерывна. 12. Теоремы Ролля и Лагранжа (без доказательства). Геометрическая интерпретация этих теорем. Теорема Ролля. Пусть ф-ция y=f(x) удовлетворяет след-м усл-ям: 1)непрерывна на отр.[а;b]; 2)дифференцируема на инт-ле(а;b); 3)на концах отрезка принимает равные зн-я,т.е. f(a)=f(b). Тогда внутри отрезка сущ-ет по крайней мере одна такая точка ξпринал.(а,b), в кот.производная ф-ция равна нулю:f’(ξ)=0. Геом.смысл т.Ролля: Если выполнены усл-я теоремы, то внутри отрезка [а;b] найдётся хотя бы одна точка, в кот. касат-я к гр-ку ф-ции будет ||-на оси абсцисс;в этой точке производная и будет равна нулю. Теорема Лагранжа. Пусть ф-ция y=f(x) удовлетвор.след-м усл-ям: 1)непрерывна на отр. [а;b]; 2)дифференцируема на инт-ле(а;b); Тогда внутри отрезка сущ-ет по крайней мере одна такая точка ξпринал.(а,b), в кот.производная равна частному от деления приращения ф-ции на приращение аргумента на этом отрезке, т.е. f’(ξ)=(f(b)-f(a))/b-a. Геом.смысл т.Лагранжа:внутри отр. [а;b] найдётся хотя бы одна точка ξпринад.(а,b),в кот. касательная к гр-ку ф-ции, проведённая через т.ξ будет ||-на секущей (АВ). 13. Достаточные признаки монотонности функции (один из них доказать). Тео-ма (достаточное условие возр.фун-и). Если производная диф-мой фун-и положительна внутри некоторого промежутка Х, то она возр.на этом промежутке.Док-во: Рас-трим два знач-я x1 и x2 на данном промежутке Х. Пусть x2>x1, x1,x2 принадл-ит Х.Докажем, что f(x2)>f(x1). f(x2)-f(x1)=f’(a)(x2-x1),где х1 Тео-ма (достаточное условие убыв.фун-и). Если производная диф-мой фун-и отрицательна внутри некоторого промежутка Х, то она убывает на этом промежутке. 14. Определение экстремума функции одной переменной. Необходимый признак экстремума (доказать). Опр.экстремума ф-ции одной пер-ной. Экстремум-это максимум и минимум ф-ции. Опр1:Точка х0 наз-ся точкой максимума ф-ции f(x),если в некоторой окрестности точки х0 выполняется неравенство f(x)≥f(x0). Опр2:Точка х1 наз-ся точкой максимума ф-ции f(x),если в некоторой окрестности точки х1 выполн-ся неравенство f(x)≤f(x1). Значения ф-ции в точках х0 и х1 наз-ся соотв-но максимумом и минимумом ф-ции. Максимум и минимум ф-ции объединяются под общим названием экстремума ф-ции. На одном промежутке ф-ция может иметь несколько экстремумов,причём может случиться, что минимум в одной т-ке больше максимума в другой fmin(x2)>fmax(x0),см. рис. X2 X1 f(x2) f(x1) f(x0) X0 Необходимое усл-е экстремума. Для того, чтобы ф-ция y=f(x) имела экстремум в точке х0, необходимо, чтобы её производная в этой точке равнялась 0 (f’(x0)=0) или не существовала. Точки, в кот.выполнено необх.усл-е экстремума,т.е. производная равна нулю или не сущ-ет, наз-ся критическими (или стационарными). Эти точки должны входить в обл.определения ф-ции.(Если в точке х0 дифференцируемая функция y=f(x) имеет экстремум, то в нек-ой окрестности этой точки выполнены условия тео-мы Ферма, и, следовательно, производная фун-и в этой точке равна нулю.Т.е.f’(x0)=0. Но фун-я может иметь экстремум и в точках, в которых она не дифференцируема.) Первое достаточное условие экстремума. Теорема. Если при переходе через точку х0 производная диф-мой фун-и y=f(x) меняет свой знак с плса на минус, то точка х0 есть точка максимума фун-и y=f(x), а если с минуса на плюс, - то точка минимума. Доказательство. Пусть производная меняет знак с плюса на минус, т.е. в некотором интервале (а, х0) производная положительна (f’ (x) >0), а в некотором интервале (х0, b) – отрицательна (f’ (x) < 0). Тогда в соответствии с достаточным условием монотонности функции f(x) возрастает на интервале (а, х0) и убывает на интервале (х0, b). По определению возрастающей функции f(x0) > f(x) при всех х принадлежащем (а, х0), а по определению убывающей функции f(x) < f(x0) при всех х принадлежащем (х0, b), т.е. f(x0)≥f(x) при всех х принадлежащем(а, b), следовательно, х0 – точка максимума функции y=f(x). Второе достаточное условие экстремума. Теорема. Если первая производная f’(x) дважды дифференцируемой функции равна нулю в некоторой точке х0, а вторая производная в этой точке f”(x0) положительна, то х0 есть точка минимума функции f’(x); если f”(x0) отрицательна, то в x0 – точка максимума. Доказательство. Пусть f’(x0) =0, а f” (x0) >0. Это означает, что f” (x) = (f’(x0))’ >0 также и в некоторой окрестности точки х0, т.е. f’(x) возрастает на некотором интервале (a, b), содержащую точку х0. Но f’(x0) =0, следовательно, на интервале (а, х0) f’ (x) >0, т.е. f’ (x) при переходе через точку х0 меняет знак с минуса на плюс, т.е. х0 – точка минимума. 15. Достаточные признаки существования экстремума (доказать одну из теорем). Первое достаточное условие экстремума. Теорема. Если при переходе через точку х0 производная диф-мой фун-и y=f(x) меняет свой знак с плса на минус, то точка х0 есть точка максимума фун-и y=f(x), а если с минуса на плюс, - то точка минимума. Доказательство. Пусть производная меняет знак с плюса на минус, т.е. в некотором интервале (а, х0) производная положительна (f’ (x) >0), а в некотором интервале (х0, b) – отрицательна (f’ (x) < 0). Тогда в соответствии с достаточным условием монотонности функции f(x) возрастает на интервале (а, х0) и убывает на интервале (х0, b). По определению возрастающей функции f(x0) > f(x) при всех х принадлежащем (а, х0), а по определению убывающей функции f(x) < f(x0) при всех х принадлежащем (х0, b), т.е. f(x0)≥f(x) при всех х принадлежащем(а, b), следовательно, х0 – точка максимума функции y=f(x). Второе достаточное условие экстремума. Теорема. Если первая производная f’(x) дважды дифференцируемой функции равна нулю в некоторой точке х0, а вторая производная в этой точке f”(x0) положительна, то х0 есть точка минимума функции f’(x); если f”(x0) отрицательна, то в x0 – точка максимума. Доказательство. Пусть f’(x0) =0, а f” (x0) >0. Это означает, что f” (x) = (f’(x0))’ >0 также и в некоторой окрестности точки х0, т.е. f’(x) возрастает на некотором интервале (a, b), содержащую точку х0. Но f’(x0) =0, следовательно, на интервале (а, х0) f’ (x) >0, т.е. f’ (x) при переходе через точку х0 меняет знак с минуса на плюс, т.е. х0 – точка минимума. 16. Понятие асимптоты графика функции. Горизонтальные, наклонные и вертикальные асимптоты. Примеры. Опр. Асимптотой гра-ка фун-и y=f(x) наз-ся прямая, обладающая тем свой-вом, что расстояние от точки (x, f(x)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. Теорема 1. Пусть функция y=f(x) определена на некоторой окрестности точки х0 (исключая, возможно, саму эту точку) и хотя бы один из переделов функции при х-> х0 +0 (справа) равен бесконечности, т.е. lim при х стремящимся к х0 –(+) 0 = бесконечность. Тогда прямая х=х0 является вертикальной асимптотой графика функции y=f(x). Теорема 2. Пусть фун-я y=f(x) определена при достаточно больших х и сущ. конечный предел фун-и lim при х стремящимся к бесконечности f(x) = b. Тогда прямая y=b есть горизонтальная асимптота графика фун-и y=f(x). Теорема 3. Пусть фун-я y=f(x) определена при достаточно больших х и существует конечные пределы lim при х стремящ-ся к беско-ти f(x)/x = k и lim прия х стремящ-ся к беско-ти [f(x) – kx] = b. Тогда прямая y=kх+b явл-ся наклонной асимптотой графика фун-и y=f(x). 17. Общая схема исследования функций и построения их графиков. Пример. Общая схема исследования функций и построение их графиков. Пример. 1. область определения. Точки разрыва. 2. если есть точки разрыва, то находим ВА 3. исследуем поведение функций при x→∞, т.е. находим ГА 4. y’. y’=0, схема знаков производных между критическими точками, устанавливаем точки экстремума 5. точки пересечения гр.функций с осями 0х и 0у 6. исследование на четность/нечетность функции Исследовать и построить график у = е 2х-х2 1.d (у)= (-∞ж+∞) 2. е 2х - х2= е-х2 = е-∞=0 d =0- ГА 3.у’= (е 2х - х2)’= е 2х - х2*(2-2х) у’ =0 2-2х=0 х=1 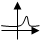 18. Функции нескольких переменных. Примеры. Частные производные (определение). Экстремум функции нескольких переменных и его необходимые условия. Опр. Пусть имеется n переменных величин, и каждому набору их значений из некоторого множества Х соответствует дно вполне определенное значение переменной величины z. Тогда говорят, что задана фун-я нескольких переменных z=f(x1, …, xn). Пример: Фун-я z=a1x1 + a2x2 +…+ anxn + b, где a, b – постоянные числа, наз-ся линейной. Опр. Частной производной фун-и нескольких переменных по одной из этих переменных наз-ся предел отношения соответствующего частного приращения фун-и к приращению рассматриваемой независимой переменной при стремлении последнего к нулю (если этот предел существует). Опр. Точка M (x0, y0) наз-ся точкой максимума (минимума) фун-и z=f(x,y), если сущ-ет окрестность точки Mб такая, что для всех точек (x,y) из этой окрестности выполняется неравенство f (x0, y0) ≥ f(x, y), (f (x0, y0) ≤ f(x, y)). Теорема. Пусть точка (х0,y0) – есть точка экстремума диф-мой фун-и z=f(x, y). Тогда, частные производные f’x(x0, y0) и f’y(x0, y0) в этой точке равны нулю. Точки, в которых выполнены необходимые условия экстремума z=f(x, y), т.е. частные производные z’x и z’y равны нулю, называются критическими или стационарными. 19. Понятие об эмпирических формулах и методе наименьших квадратов. Подбор параметров линейной функции (вывод системы нормальных уравнений). Метод наименьших квадратов. Дана экспериментальная зависимость
n-экспериментальных точек Суть метода наименьших квадратов
Формулы, служащие для аналитического представления опытных данных, получили название эмпирических формул.
(y1-f(x1))2+(y2-f(x2))2+(yn-f(xn))2→min Пусть в качестве функции y=f(x) взята линейная функция y=ax+b и задача сводится к отысканию таких значений параметров a и b, при которых функция S = ∑(axi+b-yi)2 принимает наименьшее значение i=1 заметим, что функция S=S(a,b)есть функция 2 ух переменных a и b, а xi ;yi – постоянные числа, найденные экспериментально. Т.о. для нахождения прямой решим систему S’a=0 S’b=0 Или ∑2(axi+b-yi) xi=0 ∑2(axi+b-yi) =0 После алгебраических преобразований эта система принимает вид (∑xi2)a+(∑xi)b= ∑xi yi (∑xi)a+ nb=∑ yi (1) Система называется системой нормальных уравнений Эта система имеет единственное решение т.к. ее определитель =׀А׀ ∑ xi2∑xi = n∑ xi2 -(∑xi)2 ≠0 ∑xi n Найдем частные производные (1) S”aa=2∑ xi2=A S”ab=2∑ xi=B ЫЭии=2т=С Выражение ∆=ФИ-С2 = 4 (т∑ чш2-∑ чш)2Ю0 |
