Математика Обыкновенные дроби. Понятие об обыкновенной дроби
 Скачать 0.67 Mb. Скачать 0.67 Mb.
|
|
Тема: Сложение и вычитание дробей с одинаковыми знаменателями. Цели урока: изучить новый материал, научить складывать и вычитать дроби с одинаковыми знаменателями, развивать математическую речь, внимание, воспитывать аккуратность, интерес к предмету, активность, усидчивость Ход урока. 1. Организационный момент. Друзья мои! Я очень рада Войти в приветливый ваш класс И для меня уже награда Вниманье ваших умных глаз. 2. Мотивация урока. Начать наш урок хочу пословицей. Прочитайте её. Как вы понимаете смысл пословицы? МАТЕМАТИКЕ УЧИТЬСЯ – ВСЕГДА ПРИГОДИТЬСЯ. 2) Ребята, а зачем заниматься математикой? Не зря говорят: МАТЕМАТИКА – КОРОЛЕВА НАУК! БЕЗ НЕЁ НЕ ЛЕТЯТ КОРАБЛИ, БЕЗ НЕЁ НЕ ПОДЕЛИШЬ НИ АКРА ЗЕМЛИ, ДАЖЕ ХЛЕБА НЕ КУПИШЬ, РУБЛЯ НЕ СОЧТЁШЬ, ЧТО ПОЧЁМ, НЕ УЗНАЕШЬ, А УЗНАВ, НЕ ПОЙМЁШЬ! Над какой темой мы работали на предыдущих уроках? Как вы думаете, всё ли вы знаете о дробях? Хотите узнать новое? Не боитесь трудностей? А что (кто) поможет вам справиться с трудностями? Пожелайте друг другу удачи. 3. Актуализация опорных знаний. Проверка д/з. 1) Из двух дробей с одинаковыми знаменателями меньше та, у которой а) больше числитель; б) меньше числитель; в) среди ответов нет правильных 2). Расставьте в порядке возрастания дроби: 3). Расставьте дроби в порядке убывания: 4). Найдите ошибку в записях: а) 5). Дробь, в которой числитель меньше знаменателя, называют а) правильной дробью б) неправильной дробью г) среди ответов нет правильных 6). При каких значениях, а дробь 7). Может ли правильная дробь быть больше, чем 1? Решить № 708, 709, 710. 4. Изучение нового материала. Буханку хлеба разделили на 8 равных частей (долей) (на доске висит наглядность). Сначала на тарелку положили 2 доли, а потом еще 5 долей. На тарелке оказалось 7 долей, то есть - При сложении дробей с одинаковыми знаменателями числители складывают, а знаменатель оставляют тот же. С помощью букв правило сложения можно записать так: - Буханку хлеба разрезали на 8 равных частей. - На тарелку положили 7 долей, а потом 4 доли съели. Осталось три доли, то есть - При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатель оставляют тот же. С помощью букв правило вычитания можно записать так: Как складывают дроби с одинаковыми знаменателями? При сложении дробей с одинаковыми знаменателями числители складывают а знаменатель оставляют тот же. - Как вычитают дроби с одинаковыми знаменателями? При вычитании дробей с одинаковыми знаменателями из числителя уменьшаемого вычитают числитель вычитаемого, а знаменатель оставляют тот же. - Запишите правила сложения и вычитания дробей с одинаковыми знаменателями с помощью букв. 5. Закрепление нового материала. Решить № 718, 820, 724. 6. Зарядка для глаз (Звучит музыка) Реснички опускаются... Глазки закрываются... Мы спокойно отдыхаем... Сном волшебным засыпаем... Дышится легко... ровно... глубоко... Наши руки отдыхают... Отдыхают... Засыпают... Шея не напряжена И рассла-бле-на... Губы чуть приоткрываются... Все чудесно расслабляется... Дышится легко... ровно... глубоко... (Пауза.) Мы спокойно отдыхаем... Сном волшебным засыпаем... (Громче, быстрей, энергичней.) Хорошо нам отдыхать! Но пора уже вставать! Крепче кулачки сжимаем. Их повыше поднимаем. Пoтянулись! Улыбнулись! 7. Самостоятельная работа. Решить № 722, 399 (3). 8. Итоги урока. Рефлексия. Д/з. - Что нового узнали на уроке? - Чему научились? - Оцените свои знания по таблице: Знаю: (что такое умножение) Сомневаюсь: Не знаю: Выучить п. 24. Решить № 711, 719. 721, 723. Тема: Сложение и вычитание дробей с одинаковыми знаменателями. Цели урока: закрепить правила сложения и вычитания дробей с одинаковыми знаменателями, развивать математическую речь, внимание, память; воспитывать аккуратность, интерес к предмету, активность, усидчивость. Ход урока. 1. Организационный момент. Здравствуйте, садитесь! Я знаю каждый в классе гений, Но без труда талант не впрок Скрестите шпаги ваших мнений Мы вместе сочиним урок! Мои соавторы и судьи, Оценкой вас не накажу За странный слог не обессудьте, 2. Мотивация урока. 3. Актуализация опорных знаний. Проверка д/з. - Как складывают дроби с одинаковыми знаменателями? - Как вычитают дроби с одинаковыми знаменателями? - Запишите правила сложения и вычитания дробей с одинаковыми знаменателями с помощью букв. Вычислить: 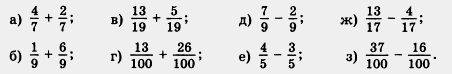 Найти значения выражений: 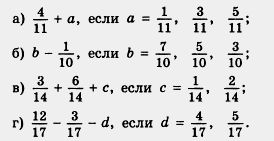 4. Решение упражнений на сложение и вычитание дробей с одинаковыми знаменателями. Решить № 726, 725, 728. 5. Физкультминутка. Поднимает руки класс - это "раз" Повернулась голова - это "два" "Руки вниз, вперёд смотри - это "три". Руки в стороны пошире развернули на "четыре" С силой их к плечам прижать - это "пять" Всем ребятам надо сесть - это "шесть". 6. Самостоятельная работа. Решить № 730 (1). 7. Итоги урока. Рефлексия. Д/з. Решить № 727, 729. Тема: Дроби и деление натуральных чисел. Цели урока: обобщить понятие обыкновенной дроби, развивать математическую речь, внимание, память; воспитывать аккуратность, интерес к предмету, активность, усидчивость. Ход урока. 1. Организационный момент. Эмоциональный настрой на урок. Дети, вам тепло? (Да!) В классе светло? (Да!) Прозвенел уже звонок? (Да!) Уже закончился урок? (Нет!) Только начался урок? (Да!) Хотите учиться? (Да!) Значит можно всем садиться! 2. Мотивация урока. 3. Актуализация опорных знаний. Проверка д/з. Вспомним определения правильных и неправильных дробей. И поиграем в игру «Хлопушка». Я читаю дроби, а если вы услышали среди них неправильную дробь, то ваша задача хлопнуть. Расположить числа в порядке возрастания. В порядке убывание Какая из точек лежит на координатном луче левее? А 4. Изучение нового материала. Разделим 2 одинаковых яблока между тремя детьми. Число 2 не делится нацело на 3. Поэтому разделим каждое яблоко на 3 равные части и дадим каждому ребенку по одной части от каждого яблока. Каждая часть — это Дробь получилась при делении 2 яблок на 3 равные части. Поэтому черту дроби можно понимать как знак деления: С помощью дробей можно записать результат деления двух любых натуральных чисел. Если деление выполняется нацело, то частное является натуральным числом. Если же разделить нацело нельзя, то частное является дробным числом. Например, Запишем число 3 в виде дроби со знаменателем 5. Для этого надо найти такое число, при делении которого на 5 получилось бы 3. Таким числом является 3 • 5, то есть 15. Значит, Запишите в виде дроби частные: 2:5; 1 : 10; 15 : 8; 7:1; 20 : 4; 77: 10 5. Закрепление нового материала. Решить № 733. 735, 737, 740. 6. Самостоятельная работа. Решить № 812 (1). 7. Итоги урока. Рефлексия. Д/з. Каким числом является частное, если деление выполняется нацело? Каким числом является частное, если деление не выполняется нацело? Выучить п.25, решить № 734, 736, 738. Тема: Смешанные числа. Цели: образовательные: совершенствовать навыки учащихся в работе с обыкновенными дробями, закрепить навыки выделения целой части из неправильной и представления смешанного числа в виде неправильной дроби; проверить знания и умение учащихся по изученному материалу. развивающие: развитие логического мышления, памяти, внимания, развития самостоятельности. воспитательные: развитие интереса к предмету, формирование умения осуществлять самоконтроль. Ход урока. 1. Организационный момент. Здравствуйте, ребята! Прошу занять свои места. Слушайте меня внимательно, На вопросы отвечайте, Всё, ребята, подмечайте, Ничего не забывайте, Меня, прошу, не подкачайте. 2. Мотивация урока. А знаете ли вы, что названия “числитель” и “знаменатель” ввёл в употребление греческий учёный-математик Максим Плануд. Долгое время дроби считались самым трудным разделом математики. У нас есть поговорка: “попал в тупик”, т.е. попал в такое положение, откуда нет выхода. У немцев аналогичная поговорка гласит: “попасть в дроби”. Она означает, что человек, попавший в “дроби”, оказался в затруднительном положении. Но сегодня на уроке мы докажем, что дроби не смогут нас поставить в трудное положение. 3. Актуализация опорных знаний. Проверка д/з. Каким числом является частное, если деление выполняется нацело? Каким числом является частное, если деление не выполняется нацело? 1. Вычислить: 2/9+5/9; 4/12+6/12; 9/15 – 6/15; 12/18 – 10/18; 2. Найти ошибку: а) правильные дроби: 3/7; 3/3; 18/9; 1/5; 4 3/8; 5. б) 3/4меньше 1/4; 10/7 больше 1; 6/6 больше 1; 3/5=1; 8/7 меньше 1; 3. Вычислить: а) 15/19 – (2/19+3/19) (1 уч.) (10/19) 20/23 – 10/23 + 3/23 (2 уч.) (13/23) Математический диктант. Записать в тетрадь полученные ответы. Затем сравнить с ответами на доске. 1)Сколько минут в 1 часе? 2)Какую часть составляют семь часов от суток? 3)Какую часть составляет 1 метр от 1 км? 4)Записать правильную дробь со знаменателем 5. 5)Записать неправильную дробь с числителем 4. 6) 7)Незнайка решил совершить за день 10 хороших поступков. Но, к сожалению, ему удалось сделать 1 часть того, что он запланировал. Сколько хороших поступков совершил 5 Незнайка за день? 8)Знайка прочитал за день 1 части книги. Сколько надо дней, чтобы прочитать всю 4 книгу? 9)Мама купила 6 кг конфет. Витя сразу съел 2 всех конфет и у него заболел живот. 3 Сколько кг конфет съел Витя? Ответы на доске: учащиеся проверяют и подсчитывают количество правильных ответов. 60 мин; 7 ; 1 ; 1,2,3,4 ; 4 ; 5; 2; 4 дня; 4 кг. 24 1000 5 1,2,3,4 9 4. Изучение нового материала. 1)Поработайте в парах. На партах у вас по 5 конфет. Разделите их поровну. Сколько конфет получит каждый? Запишите результат на листочке. 2)Проверим, что получилось. (2 целых конфеты и 1/2 ) Что можете сказать об этой записи? (В записи есть натуральное число и правильная дробь) 3)В ответе задачи получили правильную дробь? (Да) Прочитайте число. Цель достигли? Как бы вы назвали такое число? 4)В математике такие числа называются СМЕШАННЫЕ. 5)Какая у нас тема урока? ТЕМА УРОКА: СМЕШАННЫЕ ЧИСЛА (запишем тему урока в тетрадь) 6)В словаре Сергея Ивановича Ожегова слово смешанный имеет следующие значения: а) Образовавшийся путём смешения чего-нибудь б) Составленный или составившийся из разных частей, элементов, участков. Что же мы смешиваем в нашем числе? (целое число и дробное) 7)Где мы можем проверить наши выводы? Откройте учебник на стр. 183, прочитайте правило про себя. 8)Из каких частей состоит смешанное число? (Смешанное число состоит из целой части и дробной части) Чтобы из неправильной дроби выделить целую часть, надо: разделить с остатком числитель на знаменатель; неполное частное будет целой частью; остаток (если есть) дает числитель, а делитель – знаменатель дробной части. - Как записать смешанное число в виде неправильной дроби? Чтобы представить смешанное число в виде неправильной дроби, нужно: умножить его целую часть на знаменатель дробной части; к полученному произведению прибавить числитель дробной части; записать полученную сумму числителем дроби, а знаменатель дробной части оставить без изменения. 5. Закрепление нового материала. Решить № 742, 744, 746., 759 (1). 6. Физкультминутка. Поднимает руки класс - это "раз" Повернулась голова - это "два" "Руки вниз, вперёд смотри - это "три". Руки в стороны пошире развернули на "четыре" С силой их к плечам прижать - это "пять" Всем ребятам надо сесть - это "шесть". 7. Самостоятельная работа. Решить № 759 (2), 789. 8. Итоги урока. Рефлексия. Д/з. Выучить п. 26, решить № 743, 745, 747. 1)Какую цель ставили перед собой на уроке? Добились цели? С какими числами познакомились? Из каких частей состоит смешанное число? Какую дробь можно записать в виде смешанного числа? Где будем использовать смешанные числа? 2)Кто испытывал затруднения при работе со смешанными числами? А у кого всё получалось? С каким настроением пойдёте домой? 3)Всё ли мы теперь узнали с вами о дробях? На следующем уроке продолжим знакомиться с дробями. |
