оо. Вопросы к зачету. Последовательности, их общий вид, способы задания
 Скачать 0.58 Mb.
|
|
Последовательности, их общий вид, способы задания. Числовая последовательность – это функция переменной n, которая принадлежит множеству натуральных чисел N.  Xn – общий член последовательности Последовательность можно задать несколькими способами: - Аналитически или, проще говоря, формулой. - Реккурентно. Здесь известно несколько первых членов прогрессии и есть формула, которая позволяет вычислить последующие. - Описательно, простым перечислением всех элементов последовательности. Арифметическая и геометрическая прогрессии, их общий член и частичные суммы. Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом.  Элемент a с номером n называется общим членом последовательности. А число d – разностью афифметической прогрессии. Сумма первых n членов прогрессии вычисляется по формуле: 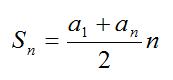 Геометрическая прогрессия – это такая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число q – знаменатель прогрессии. Сумма первых n членов прогрессии: 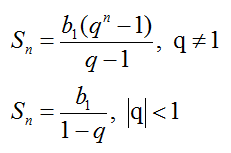 Предел последовательности. Предел последовательности – это такой объект, к которому стремятся члены последовательности с ростом порядкового номера n. Скажем иначе. Это число, в окрестности которого лежат все члены последовательности, начиная с некоторого. Переменная n в последовательностях всегда стремится к бесконечности, в сторону увеличения натуральных чисел. 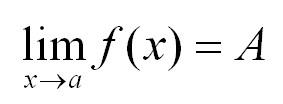 Бесконечно малые и бесконечно большие величины, ограниченные последовательности. Бесконечно малая — числовая последовательность, предел которой равен нулю. limαn=0 n→∞ Бесконечно большая — числовая последовательность, стремящаяся (равна) к бесконечности определённого знака. lim xn=∞ n→∞ Теоремы о единственности предела, о предельном переходе в неравенствах, о сжатой переменной. Теорема о единственности предела: последовательность, не может одновременно стремиться к двум различным пределам, то есть если предел последовательности существует, то он единственный. Теорема о предельном переходе в неравенствах: если элементы сходящейся последовательности {xn}, начиная с некоторого номера, удовлетворяют неравенству xn ≥ b (xn ≤ b), то и предел a этой последовательности удовлетворяет неравенству a ≥ b (a ≤ b). Теорема о сжатой переменной: Пусть даны три последовательности  ,  и  , причем   . Пусть последовательности и имеют один и тот же предел а:  . Тогда последовательность так-е имеет предел а:  Пусть даны  последовательности и существует :  :  ,  . Известно, что  . Тогда  .Связь с ограниченностью. Если последовательность имеет конечный предел, то она является ограниченной. Пределы суммы, разности, произведения, частного и степени. 1) Предел суммы двух функций равен сумме их пределов:  2) Предел разности равен разности пределов 3) Предел произведения двух функций равен произведению их пределов:  .4)Предел частного двух функций равен пределу делимого, деленного на предел делителя, если предел делителя не равен:  .5) Предел степени переменной равен той же степени предела основания  Внесем знак предела внутрь скобок, а степень останется при этом снаружи. Лемма о произведении бесконечно малой на ограниченную. Произведение бесконечно малой функции  при на ограниченную функцию есть бесконечно малая функция.Теорема о монотонной ограниченной последовательности Вейерштрасса.  Иррациональная степень, элементарные функции. Пусть  – иррациональное число, а  .Степенью числа с иррациональным показателем называется действительное число  , такое что для любых  , таких что  выполняется неравенство  , если  , и  , если  . Если же  , то полагаем  .Обозначение:  . Предел функции. Определения разных пределов. Пределы суммы, разности, произведения, частного и степени. Замечательные пределы. обозначения двух математических тождеств со взятием предела:  О маленькое.  , «о малое от  » обозначает «бесконечно малое относительно »[1], пренебрежимо малую величину при рассмотрении Непрерывность. Непрерывность суммы, разности, произведения и частного. Непрерывность сложной функции. Непрерывность обратной функции. Непрерывность элементарных функций. Теоремы Больцано-Коши и Вейерштрасса. Использование непрерывности для вычисления пределов. Ряды. Примеры геометрической прогрессии, гармонического ряда. Сходящиеся и расходящиеся ряды. Свойства: предел общего члена, умножение на число, сумма/разность, объединение членов. Положительные ряды: сравнение двух рядов, признаки Даламбера и Коши, отношение положительных рядов. Положительные ряды: переместительное свойство, произведение рядов. Знакочередующиеся ряды, признак Лейбница. Абсолютно сходящиеся ряды: определение с примерами, теорема, переместительное свойство, произведение рядов, оценка суммы и видоизмененный признак Даламбера. Производная. Определение и примеры, геометрический смысл. Дифференцируемость и непрерывность. Производные простейших элементарных функций. Производная суммы, разности, произведения и частного. Производная обратной функции. Производная сложной функции. Производная f(x)g(x) и logf(x)g(x). Таблица производных. Производная параметрически заданной функции. Теоремы Ферма, Ролля, Лагранжа и Коши. Дифференциал функции. Правило Лопиталя. Формула Тейлора (напомнить про факториалы). Первообразная и неопределенный интеграл. Свойства неопределенных интегралов. Таблица основных интегралов. Неопределенный интеграл. Метод подстановки (в обе стороны). Метод интегрирования по частям. Интегрирование рациональных функций (в общих чертах). Определенный интеграл. Определение. Достаточное условие интегрируемости. Свойства определенного интеграла. Функция верхнего предела. Формула Ньютона-Лейбница. Замена переменных. Интегрирование по частям. Примеры вычисления площади круга, объемов шара и конуса. |