Поставьте в правильной последовательности этапы решения задач регрессионного анализа
 Скачать 1.61 Mb. Скачать 1.61 Mb.
|
|
M / M / v Входящий поток – простейший, дисциплина обслуживания – с ожиданием G / G /1 Система однолинейная G / M /1 Закон распределения времени обслуж – экспоненциальный, дисциплин обс – с ожиданием M / M / v / k = v Входящий поток – простейший, дисциплина обслуживания – с явными потерями P(tож<с) – это вероятность того, что время ожидания меньше какой-то «с». При этом, чем больше P(tож<с), тем лучше качество обслуживания Зарождение теории телетрафика начало 20 века Вероятность занятия i любых линий из общего числа линий V для модели M/M/v.k=v рассчитывается по формуле Первая формула Эрланга В условиях обозначенных Кендалла установите соответствие Закон распределения времени обслуживания вызовов - v Закон распределения промежутков между вызовами - А Максимальное состояние, в котором может находится система – k Число источников нагрузки – N Вероятность занятия i любых линий из общего числа линий V для модели M/M/v,k = v,N рассчитывается по формуле Формула Энгсета Поставьте в правильной последовательности этапы решения задач регрессионного анализа: (по порядку) · Предварительная обработка экспериментальных данных – 1 · Выбор вида уравнения регрессии – 2 · Вычисление коэффициентов уравнения регрессии – 3 · Проверка адекватности построения функции результатам наблюдения – 4 С помощью какой величины определяется теснота связи в уравнении регрессии Ответ – коэффициента корреляции Компактная запись математической модели однолинейной системы с ожиданием, обслуживающую простейший поток вызовов: Ответ – M/M/1 В каких единицах измеряется интенсивность нагрузки: Ответ – Эрланг, часо-занятие в час Полнодоступный пучок из 16 линий обслуживает поток вызовов. Определить нагрузку Y, которая может поступать на этот пучок при заданной величине потерь по вызовам PB = 0,175. (Ответ округлите до ближайшего целого) Ответ: 16 На обслуживающее устройство за 5 час поступило 22 вызовов. Среднее время разговора равно 5,3 минут. Вычислить интенсивность нагрузки. Ответ: 0,39 Расчет объема оборудования производится по нагрузке: Ответ – расчетной Параметр потока (λ лямбда) является характеристикой: Ответ: числа вызывающих моментов На на однолинейную систему поступает простейший поток с параметром 15 пакетов/с. Длительность обслуживания пакетов имеет равномерное распределение в пределах 0.02…0.04 с. Найти среднее время ожидания в очереди. Ответ: 0,01273 Чему равна дисперсия случайно величины для экспоненциального распределения, если математическое ожидание равно 4. Ответ – 16 Математической моделью простейшего потока является Ответ: Pk ( t ) Свойство «выравнивания» нагрузки заключается в: Ответ – уменьшении дисперсии Коэффициент детерминации может принимать значения Ответ – от 0 до 1 Для системы с ожиданием восстановите формулу Pv=d*a/b-c Ответы: Pt это d V это b Y это c Теоретическое значение переменной – это значение, полученное по уравнению регрессии плюс ошибка регрессии Сколько параметров имеет распределение Вейбулла 2 На коммутационную систему в течение ЧНН поступает поступает 50 вызовов. Средняя длительность занятия системы каждым вызовом составляет 170 с. Определить среднее число вызовов, поступивших за время 170 c (ответ округлить до 4 десятичных знаков) Ответ: 2,3611 На обслуживающее устройство за 4 час поступило 34 вызовов. Среднее время разговора равно 5,4 минут. Вычислить интенсивность нагрузки. Ответ: 0,765 На вход двухканальной СМО с отказами поступает пуассоновский поток заявок с интенсивностью 20 выз/час. Средняя длительность обслуживания заявки 36 с. Вычислить вероятность занятия одного канала. Ответ: 0,16 В сервис-центре оператора связи один дежурный обслужил за два часа 20 клиентов, потратив на обслуживание по 120с на каждого, а второй обслужил 2 клиента, потратив по 20 минут на каждого. На какого оператора нагрузка больше? Ответ: 1 по заданному распределению найти выборочную среднюю и СКО ответ: 0,46, 0,30 На вход коммутационной системы поступает простейший поток с параметром 3 вызова в минуту. Рассчитайте минимальное количество линий, необходимых для обслуживания, при условии: - среднее время обслуживания 50 секунд - потери не должны превышать 1% Введите интенсивность нагрузки ответ: 2.5 На вход коммутационной системы поступает простейший поток с параметром 3 вызова в минуту. Рассчитайте минимальное количество линий, необходимых для обслуживания, при условии: - среднее время обслуживания 50 секунд - потери не должны превышать 1% По таблицам Пальма определите число линий Ответ: 7 На вход коммутационной системы поступает два простейших потока с математическим ожиданием 9.4 Эрл и 5.1 Эрл соответственно. На выходе ступени объединенная нагрузка распределяется пропорционально коэффициентам 0.1, 0.3, 0.6 определить среднее значение нагрузки на второе направление Ответ: 4,35 На вход коммутационной системы поступает два простейших потока с математическим ожиданием 2.0 Эрл и 6.1 Эрл соответственно. На выходе ступени объединенная нагрузка распределяется пропорционально коэффициентам 0.1, 0.3, 0.6 определить среднее значение нагрузки на первое направление ответ: 0,81 На вход одноканальной СМО поступает простейший поток заявок с интенсивностью 11 заявок в час. Среднее время обслуживания заявки 5 минуты. Вычислить вероятность занятости всех линий (ответ округляйте до сотых) ответ: 0,48 Интенсивность трафика в 150 пакетов в секунду со средней длинной пакета 81 байт поступает на выделенную линию с пропускной способностью 4 Мбит/с. Вычислить нагрузку линии (в эрлангах). Ответ округляйте до тысячных, разделитель – запятая Ответ: 0,024 На вход трехканальной АТС (с отказами) поступает пуассоновский поток заявок с параметром 5 выз/ч. Средняя длительность обслуживания заявки 12 мин. Вычислить среднюю долю времени, в течение которой АТС вообще не загружена. Ответ округляйте до тысячных ответ: 0,375 На вход двухканальной СМО с отказами поступает пуассоновский поток заявок с интенсивностью 20 выз/час. Средняя длительность обслуживания заявки 36 с. Вычислить вероятность того, что система свободна (до сотых). Ответ: 0,82 На обслуживающее устройство за 11 час поступило 32 вызовов. Среднее время разговора равно 6,1 минут. Вычислить интенсивность нагрузки. Ответ: 0,29 Задержку между двумя последовательными пакетами называют Джиттер Система из 8 каналов обслуживает 100 абонентов. Удельная нагрузка 0,06 Эрл. Определить вероятность потерь по вызовам (до тысячных) Ответ: 0,75 (не точно) Установите соответствие Флюктуация задержки IP-пакета – IPDV Коэффициент ошибок пакетов – IPER Задержка доставки IP-пакета IPLR Характеристики непрерывности об.. определяют возможность пользования полученной услугой с заданными атрибутами в течение запрошенного интервала времени На обслуживающее устройство за 4 час поступило 38 вызовов. Среднее время разговора равно 2,1 минут. Вычислить интенсивность нагрузки. Ответ: 0,3325 38:4:60*2.1 Управление очередями, осуществляемое путем: (тут не полный скрин был, что-то из этого) установление приоритетов во входящем трафике 1. сортировки входящего трафика по видам (например, по допустимым задержкам, по занимаемой ширине полосы пропускания) 2. ограничения или сброса входящей нагрузки 3. кэширования 4. распределения приоритетов во входящем трафике Характеристики доступности услуг оценивают возможность получения услуг (с заранее специфицированными допусками и с соблюдением других заданных условий) по запросу пользователя. Самоподобие речевого трафика улучшает показатели качества обслуживания. Соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями называют законом распределения Интенсивность потока является характеристикой числа вызовов По заданному эмпирическому распределению рассчитать параметр, если случайная величина Х распределена по закону Пуассона Х 0 1 2 3 4 N 250 200 100 50 10 Ответ: 0.967213115 Определить вероятность поступления точно 4 вызовов при простейшем потоке, если вызовы поступают в среднем через 15 секунд, а среднее время обслуживания одного вызова 45 секунд. Ответ округлите до двух знаков после запятой. Ответ: 0,16 На вход одноканальной СМО поступает простейший поток заявок с интенсивностью 11 заявок в час. Среднее время обслуживания заявки 5 минуты. Определите величину потерь (Ответ округляйте до сотых) ответ: 0,48 Величина коэффициента регрессии характеризует ответ: среднее изменение результата при изменении фактора на одну единицу В модели парной линейной регрессии величина У является ответ: неслучайной Статистической зависимостью называется - связь переменных, на которую накладывается воздействие случайных факторов На обслуживающее устройство за 6 часов поступило 91 вызовов. Среднее время разговора равно 8,2 минут. Вычислить интенсивность нагрузки (ответ округлить до 2 десятичных знаков) 2,07  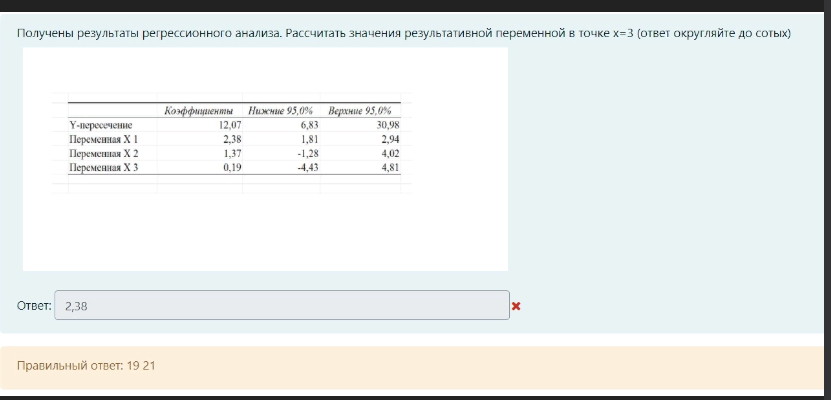    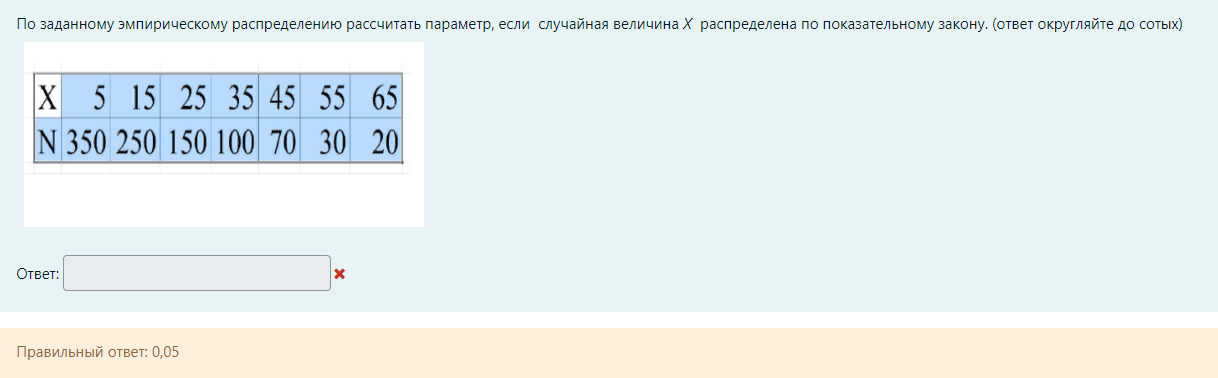 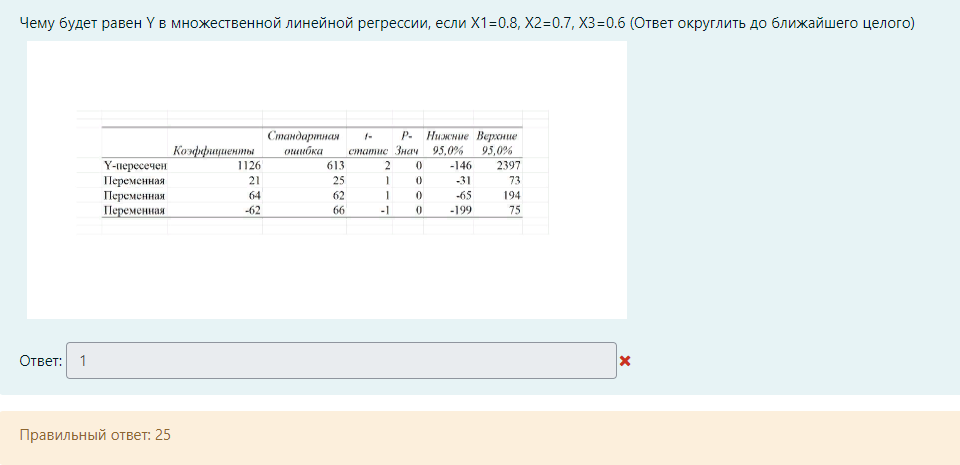 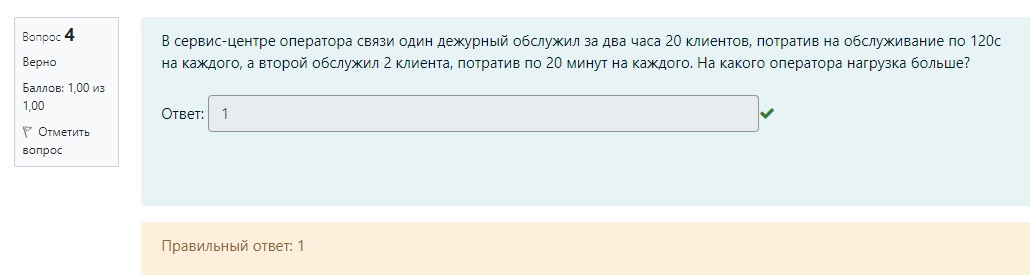  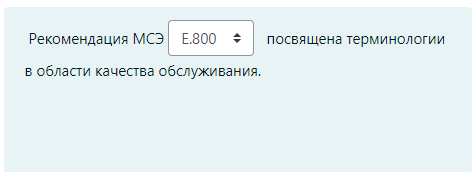 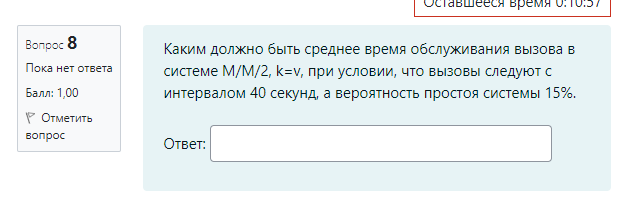 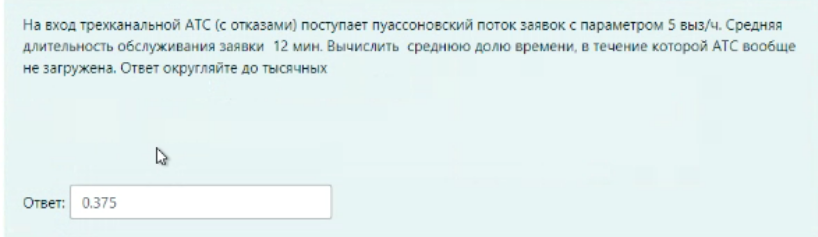 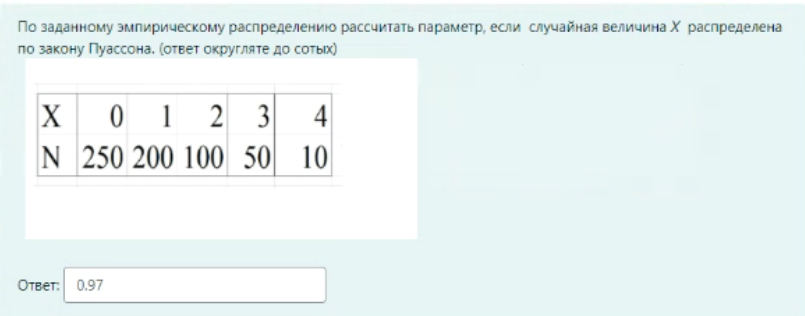  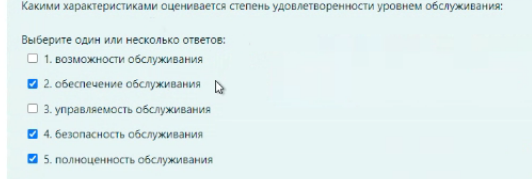 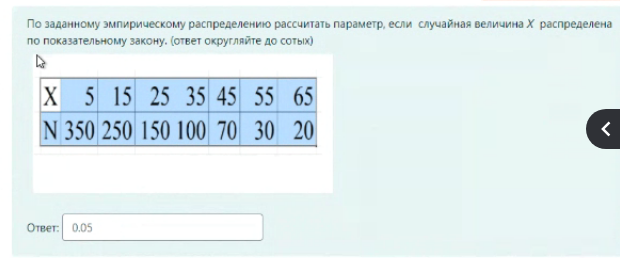     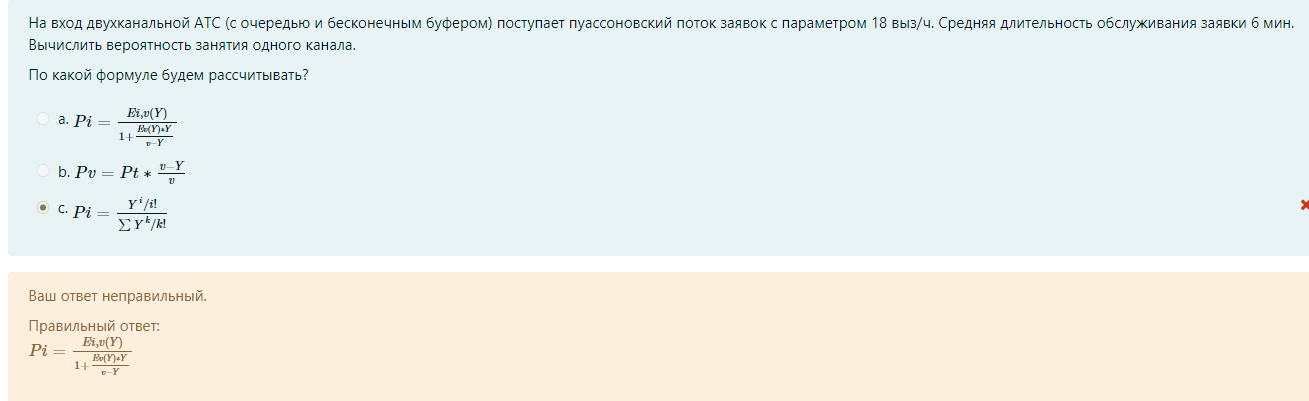 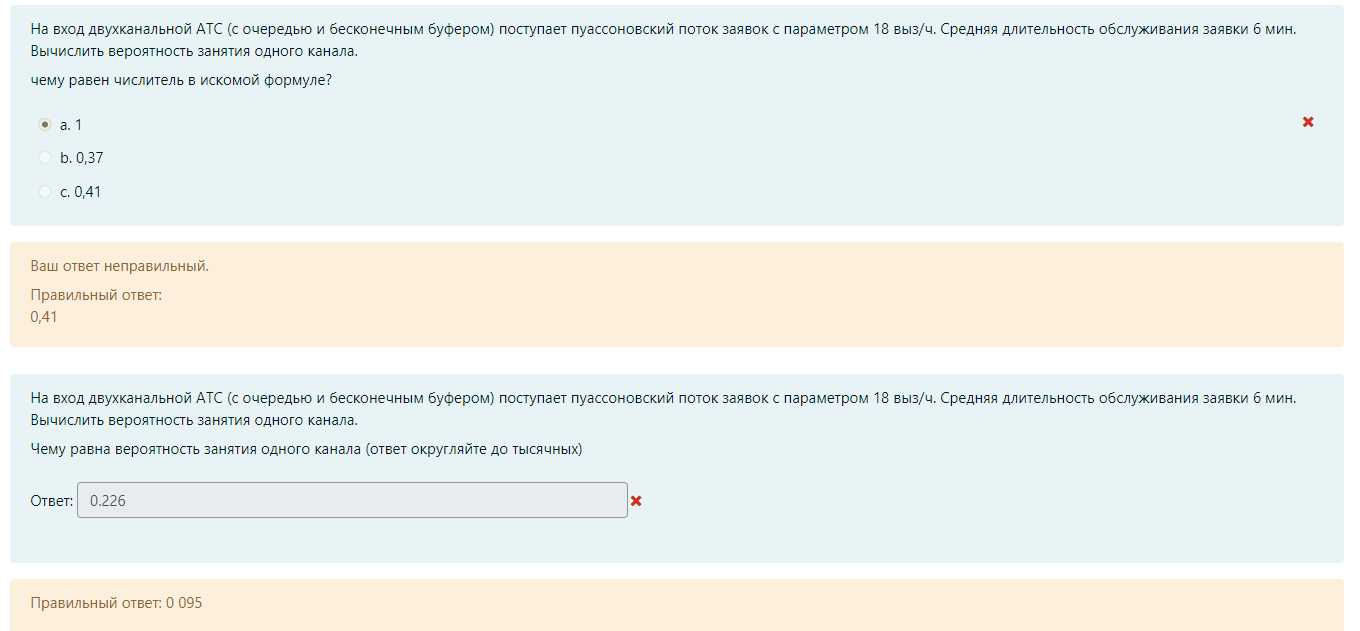 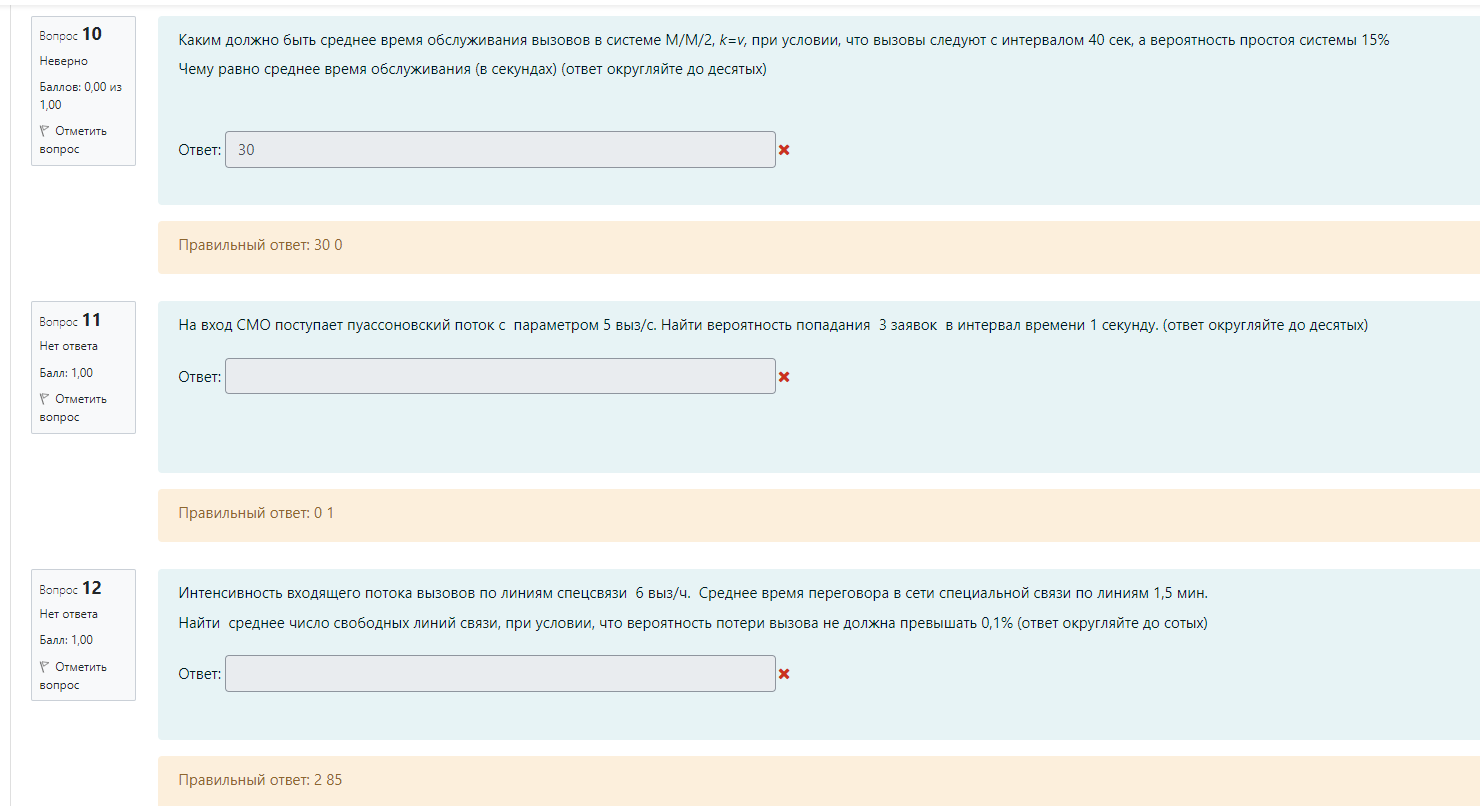 |
