ПК-1
|
ПК-1.4 Умеет собирать и анализировать данные о работе сети, статистические параметры трафика; проводить расчет интерфейсов внутренних направлений сети; вырабатывать решения по оперативному переконфигурированию сети, изменению параметров коммутационной подсистемы, сетевых платформ; изменять параметры коммутационной подсистемы, маршрутизации трафика, организации новых и расширении имеющихся направлений связи
|
|
№
|
Задание
|
Ответ
|
Вес
|
|
|
|
|
На коммутационную систему в течение ЧНН поступает 50 вызовов. Средняя длительность занятия системы каждым вызовом составляет 170 с. Определить среднее число вызовов, поступивших за время 170 c (ответ округлить до 2 десятичных знаков)
2,36
4,36
3,36
2,76
2,06
|
|
1
|
|
|
Расчитайте интенсивность нагрузки, если вызовы поступают в среднем через 7,7 секунд, а среднеее время обслуживания одного вызова 5,3секунд c (ответ округлить до 2 десятичных знаков)
0,86
0,69
0,96
1,69
|
|
1
|
|
|
На обслуживающее устройство за 3 час поступило 31 вызовов. Среднее время разговора равно 8,2 минут. Вычислить интенсивность нагрузки (ответ округлить до 2 десятичных знаков)
1,21
1,51
1,41
1,31
|
|
1
|
|
|
В каких единицах измеряется интенсивность нагрузки. Выберите один или несколько ответов:
Эрланг
часо-занятие
часо-занятие в час
проценты
промилле
|
|
1
|
|
|
Система из 8 каналов обслуживает 100 абонентов. Удельная нагрузка 0.06 Эрл. Определить вероятность потерь по вызовам.
(ответ округляйте до тысячных)
0,145
0,122
1,000
0,001
|
|
1
|
|
|
На вход коммутационной системы поступает простейший поток с параметром 3 вызова в минуту. Рассчитайте интенсивность нагрузки (ответ округляйте до десятых) при условии:
- потери не должны превышать 1%
- среднее время обслуживания 50 секунд
3,5
4,5
2,5
5,5
|
|
1
|
|
|
На полнодоступный пучок из v=9 линий поступает простейший поток вызовов с параметром 150 выз/час. Время обслуживания одного вызова распределено экспоненциально и равно 12 с. Найти потери по времени (ответ округлить до 2 десятичных знаков)
0,00
0,45
0,12
1,00
|
|
1
|
|
|
В условных обозначенных Кендалла установите соответствие
1 Закон распределения промежутков между вызовами
2 Число источников нагрузки
3 Закон распределения времени обслуживания вызовов
4 Максимальное состояние, в котором может находится система
N - 2
A - 1
K - 4
B - 3
|
|
1
|
|
|
Вероятность занятия V линий из общего числа линий V для модели M/M/v,k=v рассчитывается по формуле
Формула Энгсета
Вторая формула Эрланга
Формула Кроммелина
Первая формула Эрланга
|
|
1
|
|
|
Вероятность занятия V линий из общего числа линий V для модели M/M/v,k=v,N рассчитывается по формуле
Формула Энгсета
Вторая формула Эрланга
Формула Кроммелина
Первая формула Эрланга
|
|
1
|
|
|
Выберите математическую модель системы с ожиданием, учитывающую простейший поток вызовов.
G/M/1
M/D/1
M/M/v,k=v
M/M/v
M/M/v,k=v,N
|
|
1
|
|
|
Расчет объема оборудования производится по нагрузке
Расчетной
ЧНН
средней
|
|
1
|
|
|
На обслуживающее устройство за 4 час поступило 38 вызовов. Среднее время разговора равно 2,1 минут. Вычислить интенсивность нагрузки. (ответ округлить до 2 десятичных знаков)
0,33
0,43
0,53
0,23
|
|
1
|
|
|
Свойство «выравнивания» нагрузки заключается в:
увеличении дисперсии
уменьшении дисперсии
неизменности дисперсии
|
|
1
|
|
|
Определить вероятность поступления точно 4 вызовов при простейшем потоке, если вызовы поступают в среднем через 15 секунд, а среднее время обслуживания одного вызова 45 секунд. (ответ округлить до 2 десятичных знаков)
0,19
0,26
0,16
0,29
|
|
1
|
|
|
На вход двухканальной СМО с отказами поступает пуассоновский поток заявок с интенсивностью 20 выз/ч. Средняя длительность обслуживания заявки 36 с. Вычислить вероятность занятия одного канала (ответ округлить до 2 десятичных знаков)
0,02
0,20(0,16)
0,22
0,05
|
|
1
|
|
|
Параметр потока (λ) является характеристикой:
числа вызовов
числа промежутков между вызовами
числа вызывающих моментов
|
|
1
|
|
|
В модели M/D/v дисперсия времени обслуживания равна:
0
1/λ
λ
1/λ2
|
|
1
|
|
19
|
В системах с явными потерями длина очереди (j) принимает значение:
j>0
Отсутствует
j=0
|
|
1
|
|
20
|
Число состояний СМО с ожиданием определяется:
k=i
k=j
k=v+j
|
|
1
|
|
21
|
Математической моделью простейшего потока является:
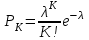
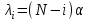
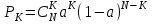
|
|
1
|
|
22
|
Математической моделью примитивного потока является:
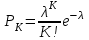
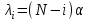
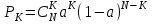
|
|
1
|
|
23
|
1-я формула Эрланга записывается в виде:
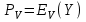
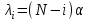
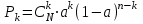
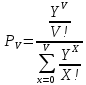
|
|
1
|
|
24
|
Расчетная нагрузка связана со средней следующим соотношением:
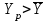
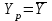
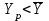
|
|
1
|
|
25
|
Для стационарных и ординарных потоков параметр (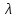 ) и интенсивность ( ) и интенсивность (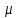 ) связаны: ) связаны:
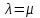
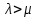
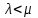
|
|
1
|
|
26
|
В формуле 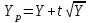 величина (t): величина (t):
коэффициент пропорциональности
коэффициент корреляции
коэффициент доверия
|
|
1
|
|
27
|
Функция распределения промежутков между вызовами простейшего потока имеет распределение:
показательное
нормальное
вейбулла
|
|
1
|
|
28
|
Какие основные составляющие включают в математические модели систем распределения информации
входящий поток вызовов
схему системы распределения информации
исходящий поток вызовов
дисциплина обслуживания
|
|
1
|
|
29
|
Как изменяется пропускная способность в полнодоступном пучке линий с увеличением величины потерь ( V= const):
увеличивается
уменьшается
не изменяется
|
|
1
|
|
30
|
Как изменяется пропускная способность в полнодоступном пучке линий с увеличением емкости этого пучка (Р=const)?
увеличивается
уменьшается
не изменяется
|
|
1
|
|
31
|
Каковы соотношения Рв, Рv в полнодоступном пучке, обслуживающем вызовы простейшего потока, дисциплина обслуживания явные потери?
Рв = Рv
Рв > Рv
Рв < Рv
|
|
1
|
|
32
|
Каковы соотношения Рн, Рв, Рt, Рv в полнодоступном пучке, обслуживающем вызовы примитивного потока, дисциплина обслуживания явные потери?
Рв = Рv
Рв > Рv
Рв < Рv
|
|
1
|
|
33
|
Если среднее число одновременно занятых линий равно 5, чему равна интенсивность обслуженной нагрузки
10
5
1
|
|
1
|
|
34
|
Если среднее число одновременно занятых линий равно 5, чему равна пропускная способность системы распределения информации?
5
1
10
|
|
1
|
|
35
|
Как изменяется средняя длина очереди в системе M /M/ v с увеличением числа линий
увеличивается
уменьшается
не изменяется
|
|
1
|
|
36
|
Одинарным поток заявок является в том случае, когда за малый промежуток времени вероятность поступления более чем одной заявки близка к:
0
1
0,5
|
|
1
|
|
37
|
Рассчитать среднюю интенсивность вызовов, поступающих диспетчеру, если поступило 120 вызовов в течение суток
4
5
6
|
|
1
|
|
38
|
На вход одноканальной системы поступает простейший поток с параметром 4 вызова в час. Время является случайной величиной, распределенной в соответствии с законом Вейбула. Среднее время обслуживания = 3 мин., среднее квадратическое отклонение равно = 2 мин. Рассчитать среднее время ожидания в очереди (в секундах).
14,40
0,004
20,65
0,24
|
|
1
|
|
40
|
Интенсивность трафика в 50 пакетов в секунду со средней длиной пакета 47 байт поступает на выделенную линию с пропускной способностью 2 Мбит/с. Вычислить нагрузку в линии (в эрлангах).
0,001
0,009
0,091
0,012
|
|
1
|
|
41
|
Цифровая линия связи с пропускной способностью 2.048 Мбит/с в среднем принимает 128 пакетов в секунду. Пакет содержит в среднем 320 байт данных. Найдите коэффициент использования линии.
0,31
0,02
0,17
|
|
1
|
|
42
|
Какой поток вызовов называется простейшим
нестационарный ординарный поток с последействием
стационарный ординарный поток с последействием
стационарный ординарный поток без последействия
|
|
1
|
|
43
|
Среднее число заявок в произвольный момент времени в буфере системы типа M/D/1 равно 3. Чему равна дисперсия времени обслуживания заявок
2
1
0
0,5
|
|
1
|
|
44
|
Среднее число заявок в произвольный момент времени в буфере системы типа M/M/1 равно 3. Чему равна нагрузка в системе.
0,35
0,25
0,45
|
|
1
|
|
45
|
Доля времени, в течение которого все соединительные пути, доступные группе источников, заняты, называют:
потери по линиям
потери по нагрузке
потери по времени
|
|
1
|
|
46
|
Для количественной оценки качества обслуживания с ожиданием рассчитываются следующие характеристики:
среднее время ожидания по отношению ко всем поступившим вызовам
вероятность ожидания задержанного вызова свыше времени t
интенсивность поступающей нагрузки
потери по времени
|
|
1
|
|
47
|
Под пропускной способностью коммутационной системы понимается:
интенсивность потерянной нагрузки
интенсивность поступающей нагрузки
интенсивность обслуженной нагрузки
|
|
1
|
|
48
|
Для количественной оценки качества обслуживания с явными потерями рассчитываются следующие величины
среднее время ожидания по отношению ко всем поступившим вызовам
вероятность ожидания задержанного вызова свыше времени t
интенсивность поступающей нагрузки
потери по времени
|
|
1
|
|
49
|
В функции Эрланга E23(46) число линий равно
46
23
2
0,5
|
|
1
|
|
50
|
В функции Эрланга E23(46) интенсивность нагрузки
23
2
0,5
46
|
|
1
|
|
 Скачать 1.61 Mb.
Скачать 1.61 Mb.