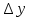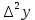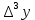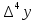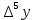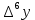Курсовая интерполяция полей. Курсовая Леша. Построенние интерполяционного многочлена
 Скачать 0.63 Mb. Скачать 0.63 Mb.
|
|
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «Тульский государственный университет» Институт прикладной математики и компьютерных наук Кафедра вычислительной техники Курсовая работа по дисциплине ЧИСЛИННЫЕ МЕТОДЫ на тему: ПОСТРОЕННИЕ ИНТЕРПОЛЯЦИОННОГО МНОГОЧЛЕНА Студент группы . _________ (Ф.И.О.) (подпись, дата) Руководитель работы _________ (Ф.И.О., должность) (подпись, дата) Комиссия: ________________________ ________________________ ________________________ Тула 2022 МИНОБРНАУКИ РОССИИ ФГБОУ ВО «Тульский государственный университет» Институт прикладной математики и компьютерных наук Кафедра «Вычислительная техника» З А Д А Н И Е На курсовой проект (курсовую работу) по дисциплине (наименование дисциплины указать полностью) ____________________________________________________________ _____________________________________________________________________________ студенту(ке) группы ____________ Ф.И.О. студента ________________________________ _____________________________________________________________________________ Тема проекта (работы) _________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________ Входные данные _____________________________________________________________ _____________________________________________________________________________ _____________________________________________________________________________ Задание получил ___________________ «______» __________________20____г. (подпись студента) Срок предоставления задания «______» ________________________ 20____г. Руководитель ___________________ ___________________________________________ (подпись) (расшифровка подписи) «__» ______________________ 20___г. К защите. Руководитель _________________ _____________________________________ (подпись) (расшифровка подписи) Замечания руководителя _______________________________________________________ __________________________________________________________________________________________________________________________________________________________ «____» _________________________ 20___г. При защите курсового проекта (работы) наличие рецензии обязательно. СОДЕРЖАНИЕ ВВЕДЕНИЕТемой курсовой работы является построение интерполяционных многочленов. Тема достаточно актуальна так как, интерполяция — это метод нахождения неизвестных промежуточных значений некоторой функции по имеющемуся дискретному набору ее известных значений. И в реальной жизни часто приходится работать с интерполяцией. И решение таких задач очень востребовано в наше время так как, интерполяция применяется в различных областях. Таких как, интерполяция поверхности осадков в метеорологии, интерполяция высот в геологии, вычисление уклонов в строительстве и во многих других областях. Целью работы является закреплением теоретических знаний по курсу «Численные методы» и изучением различных методов интерполяции. Задачи работы: - получить навык в построении интерполяционного многочлена с заданными характеристиками; - получить навык разработки программных средств для интерполяции функции, заданной таблично. В ходе выполнения курсовой работы необходимо разработать программу для интерполирования функции и фиксирования погрешности с помощью многочленов Бесселя и Стирлинга. 1. ЗАДАНИЕ Построить интерполяционные многочлены n-ой степени для функции, заданной таблично на интервале [a, b] с шагом h, используя интерполяционный многочлен Бесселя и интерполяционный многочлен Стирлинга, для функции 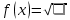 . Построить график для исходной функции. . Построить график для исходной функции. 2. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ Интерполяционные многочлены Стирлинга и Бесселя: Интерполяционные формулы — в математике формулы, дающие приближённое выражение функции 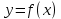 при помощи интерполяции, то есть через интерполяционный многочлен при помощи интерполяции, то есть через интерполяционный многочлен 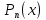 степени степени 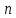 , значения которого в заданных точках , значения которого в заданных точках 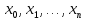 совпадают со значения совпадают со значения 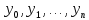 функции функции 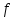 в этих точках. в этих точках. Рассмотрим задачу построения интерполяционного многочлена для функции f, заданной своими значениями 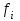 и и 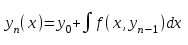 равномерной сетки с шагом h. равномерной сетки с шагом h.Пусть точка х* расположена вблизи некоторого узла, который обозначим 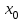 . Требуется построить интерполяционный многочлен четной степени. В качестве узлов интерполирования следует выбрать сетку, симметричную относительно узла . Требуется построить интерполяционный многочлен четной степени. В качестве узлов интерполирования следует выбрать сетку, симметричную относительно узла 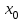 : :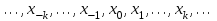 (1) (1)Для представления интерполяционных многочленов Стирлинга и Бесселя используют центральные конечные разности и средние арифметические соседних конечных разностей одного и того же порядка 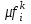 . .Центральные разности 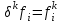 для построения центральных интерполяционных формул определяются по формулам - для построения центральных интерполяционных формул определяются по формулам -Первого порядка: 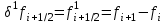 или 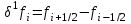 ; ;k-ого порядка 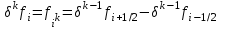 ; (2) ; (2)средние арифметические соседних конечных разностей одного и того же порядка: 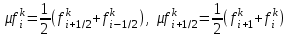 (3) (3)Интерполяционный многочлен Стирлинга от переменной t обычно обозначается 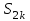 : :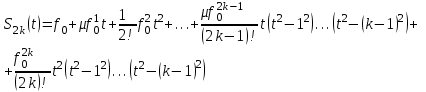 (4) (4)Пусть теперь точка интерполирования 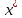 лежит между узлами лежит между узлами 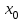 и и 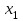 в близи точки в близи точки 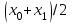 . Требуется построить интерполяционный многочлен нечетной степени. Тогда сетка, минимизирующая погрешность, симметрична относительно точки . Требуется построить интерполяционный многочлен нечетной степени. Тогда сетка, минимизирующая погрешность, симметрична относительно точки 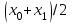 , т.е. относительно точки , т.е. относительно точки 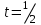 . .На сетке 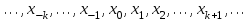 можно получить интерполяционный многочлен Бесселя, обычно обозначаемый можно получить интерполяционный многочлен Бесселя, обычно обозначаемый 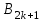 : :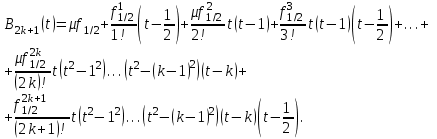 (5) (5)Итак, рассмотрено два интерполяционных многочлена: многочлен Стирлинга, который используется при построении многочлена четной степени и строится по нечетному числу узлов, и многочлен Бесселя, который используется при построении многочлена нечетной степени и строится по четному числу узлов. Если же степень многочлена фиксирована не жестко, т.е. может быть, как четной, так и нечетно, то целесообразно использовать многочлен Стирлинга в случае, когда 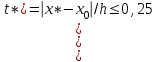 , (6) , (6)т.е. когда точка интерполирования 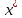 расположена ближе к узлу расположена ближе к узлу 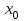 , чем к середине между узлами. Многочлен Бесселя следует использовать в случае, когда , чем к середине между узлами. Многочлен Бесселя следует использовать в случае, когда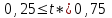 , (7) , (7)т.е. когда точка интерполирования 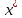 расположена ближе к середине между узлами расположена ближе к середине между узлами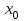 и и 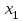 . Одно из условий (6) или (7) всегда может быть обеспечено выбором соответствующего узла в качестве . Одно из условий (6) или (7) всегда может быть обеспечено выбором соответствующего узла в качестве 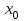 . .3. ВХОДНЫЕ И ВЫХОДНЫЕ ДАННЫЕ3.1 Входные данныеДля вычисления интерполяционного многочлена Стирлинга и Бесселя используются следующие переменные: double X* - искомое точка на отрезке интерполяции в textbox1; double a,b – нижняя и верхняя граница отрезка исследуемой функции в textBox2 и textBox3 соответственно; int n – количество заданных точек на отрезке в textBox4; int S – степень многочлена в textBox5. 3.2 Выходные данныеПо итогу выполнения программы на выход идут следующие элементы: - double Stirling – значение функции в точке X*, полученное при помощи полинома Стирлинга; - double Bassel - значение функции в точке X*, полученное при помощи полинома Бесселя; - long timeSt – время подсчета полинома Стирлинга; - long timeBs – время подсчета полинома Бесселя. 4. АЛГОРИТМЫ ПОСТРОЕНИЯ ИНТЕРПОЛЯЦИОННЫХ МНОГОЧЛЕНОВАлгоритм представлен в виде блок-схем: Блок-схема 1 - конструктора класса Function, находящий узел 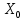 , и строящий конечные разности k-того порядка и подсчитывающий значения функции в промежутке от , и строящий конечные разности k-того порядка и подсчитывающий значения функции в промежутке от 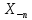 до до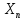 , где n – степень многочлена; , где n – степень многочлена;Блок-схема 2 – метода EndDifference(int n) функция, вычисляющая конечные разности k-того порядка. Блок-схема 3 – метода Factorial(int a)- функция, вычисляющая факториал от a. Блок-схема 4 - метода Stirling()функция, вычисляющая значение в точки при помощи интерполяционного полинома Стирлинга. Блок-схема 5 – метода Bessel()функция, вычисляющая значение в точки при помощи интерполяционного полинома Бесселя. 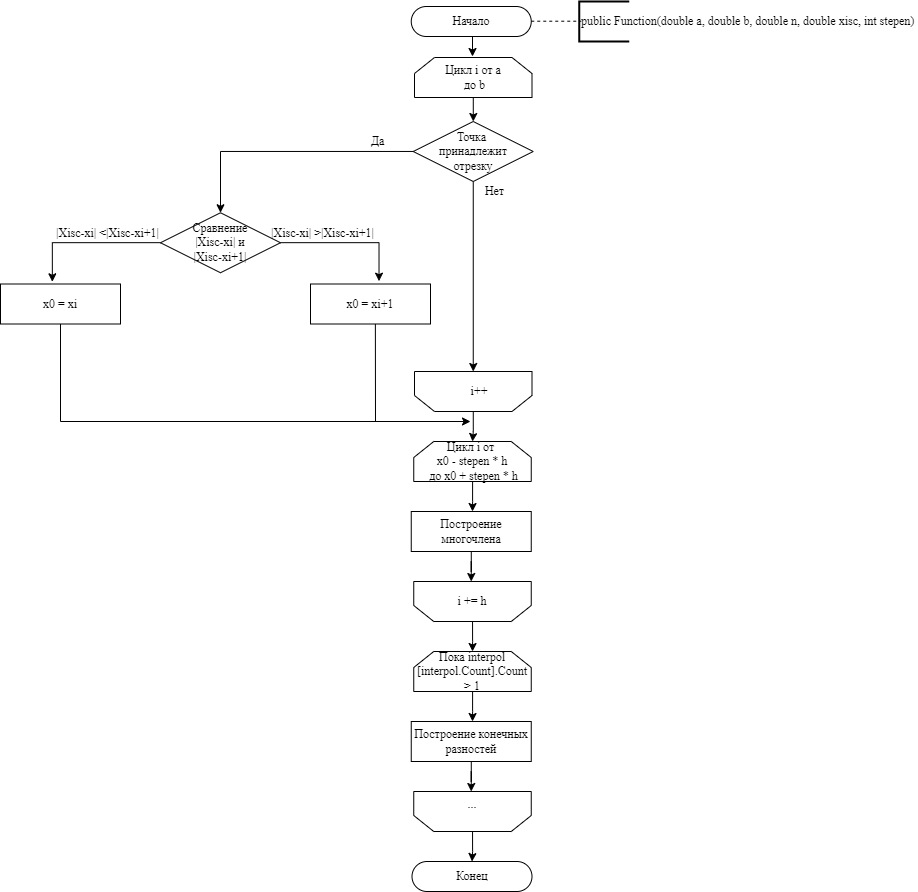 Блок-схема 1 – Конструктора класса Function 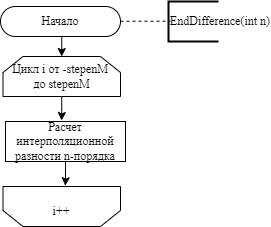 Блок-схема 2 – Метода EndDifference 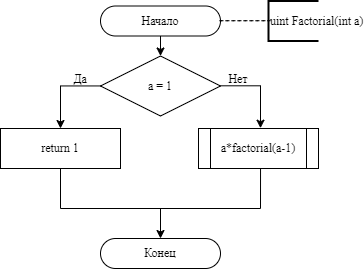 Блок-схема 3 – Метода Factorial 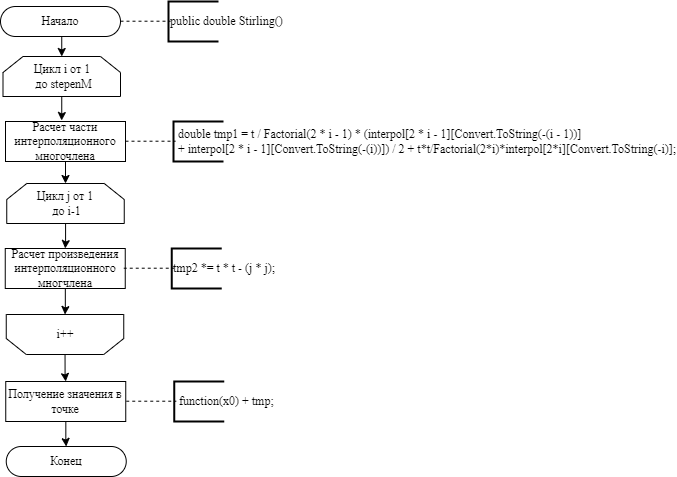 Блок-схема 4 – Метода Stirling  Блок-схема 5 – Метода Bessel 5. ОПИСАНИЕ ОСНОВНЫХ ФУНКЦИЙ ПРОГРАММЫПрограмма содержит следующие основные функции: public Function (double a, double b, int n, double xisc, int stepen)- конструктор класса Function, находящий узел 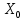 , и строящий конечные разности k-того порядка и подсчитывающий значения функции в промежутке от , и строящий конечные разности k-того порядка и подсчитывающий значения функции в промежутке от 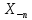 до до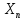 , где n – степень многочлена. , где n – степень многочлена.public void EndDifference(int n) - функция, вычисляющая конечные разности k-того порядка. ulong Factorial(int a) – функция, вычисляющая факториал от a. public double Stirling()- функция, вычисляющая значение в точки при помощи интерполяционного полинома Стирлинга. public double Bessel()- функция, вычисляющая значение в точки при помощи интерполяционного полинома Бесселя. private void Interpolation_Click(object sender, EventArgs e) – функция, вызывающая подсчет многочленов в точке и выводящая результат в таблицу. Для начала заполняются поля входные данные описанные в пункте 3 в textBox. Далее, при нажатии кнопки вызывается метод private void Interpolation_Click(object sender, EventArgs e), который сначала запускает поиск значения в точке при обоих интерполяционных многочленов. Далее происходит заполнения таблицы точных значений и построение графика по точкам, данным в диапазоне (точное значение функции) и точкам, посчитанным с помощью интерполяционных многочленов Стирлинга и Бесселя. При вызове конструктора класса, куда подается низшая и верхняя граница функции, кол-во узлов, искомая точка и степень многочлена происходит нахождение узла 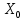 . Он определяется, как ближайший узел к . Он определяется, как ближайший узел к 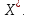 Затем происходит построение нового диапазона значений функций от 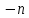 до до 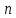 , где n степень многочлена. Это нужно, чтобы при нахождении многочлена Стирлинга в угловых точках изначального отрезка не возникала ошибка при попытке обратиться к несуществующему индексу. , где n степень многочлена. Это нужно, чтобы при нахождении многочлена Стирлинга в угловых точках изначального отрезка не возникала ошибка при попытке обратиться к несуществующему индексу.После построения нового диапазона значений строим конечные разности и запускаем алгоритм Стирлинга и Бесселя, описанных в пункте 2. 6. РЕЗУЛЬТАТЫ РАБОТЫ ПРОГРАММЫПриведем несколько примеров работоспособности программы для наглядности возьмем разное степень многочлена маленькую и большую. С помощью кнопки «Пример» у нас заполняются наши textBoxы уже заготовленными данными. После нажатия кнопки «Интерполировать» мы выводим таблицу значений X и Y в dataGridView1, график интерполяции многочлена Бесселя, интерполяционный многочлен Стирлинга и график первоначальной функции выводится в chart1, значение интерполяции Y в dataGridView2. Исходная функция 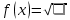 cо степенью многочлена равной трем, результат программы представлен на рисунке 1. cо степенью многочлена равной трем, результат программы представлен на рисунке 1.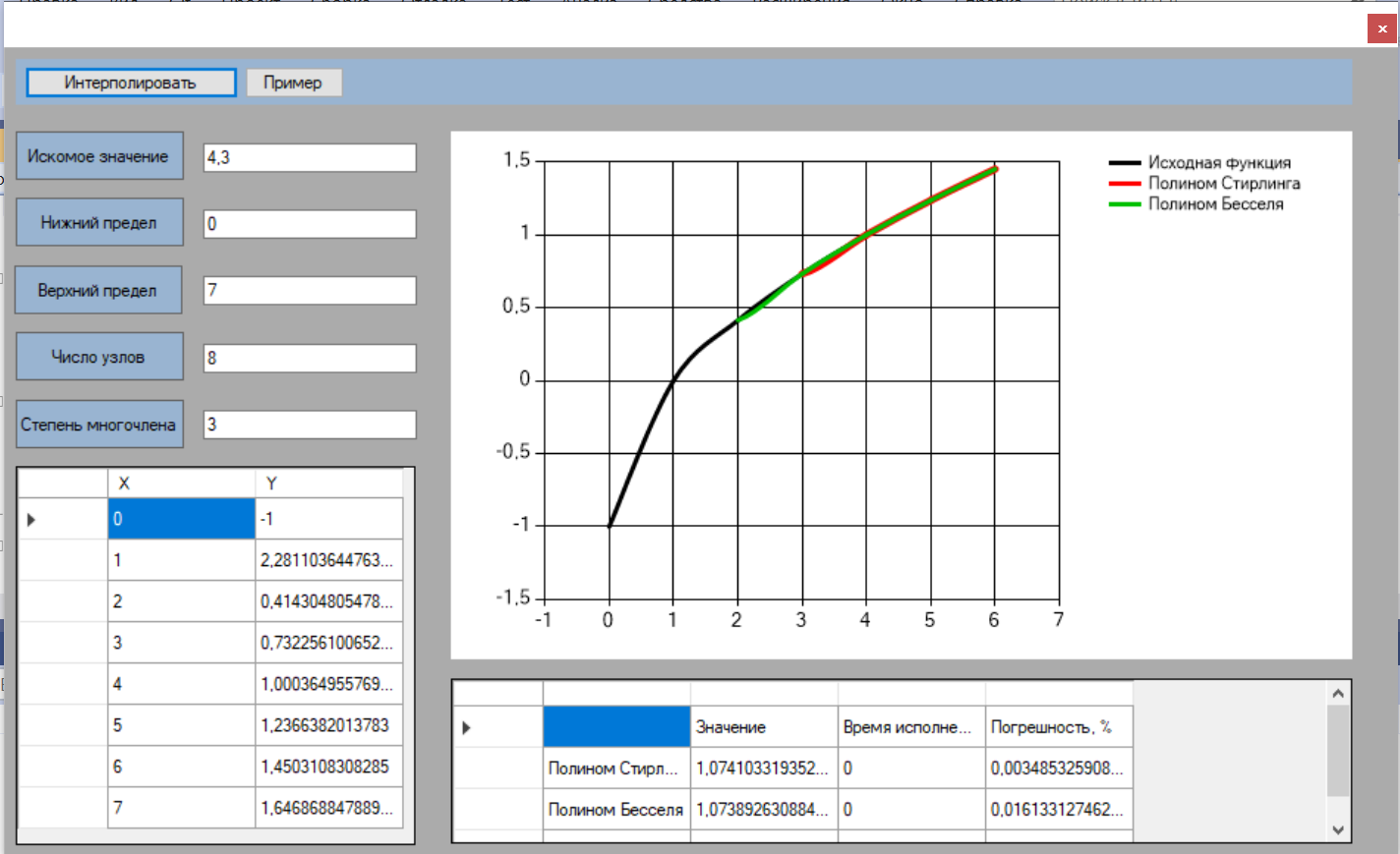 Рисунок 1 – Результат программы со степенью три Исходная функция 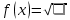 cо степенью многочлена равной семи, результат программы представлен на рисунке 2 cо степенью многочлена равной семи, результат программы представлен на рисунке 2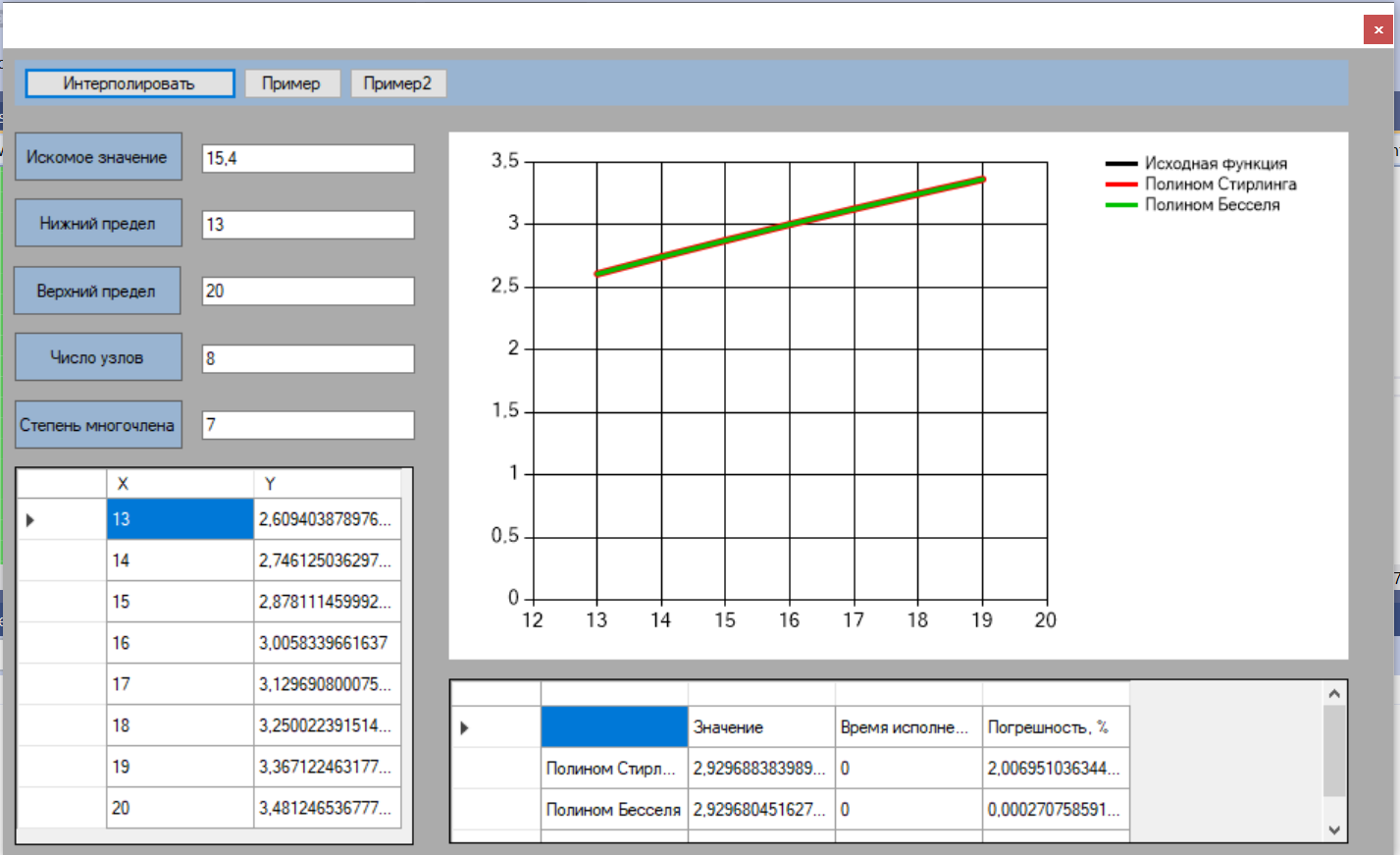 Рисунок 2 – Результат программы со степенью семь Исходная функция 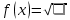 cо степенью многочлена равной десяти, результат программы представлен на рисунке 3 cо степенью многочлена равной десяти, результат программы представлен на рисунке 3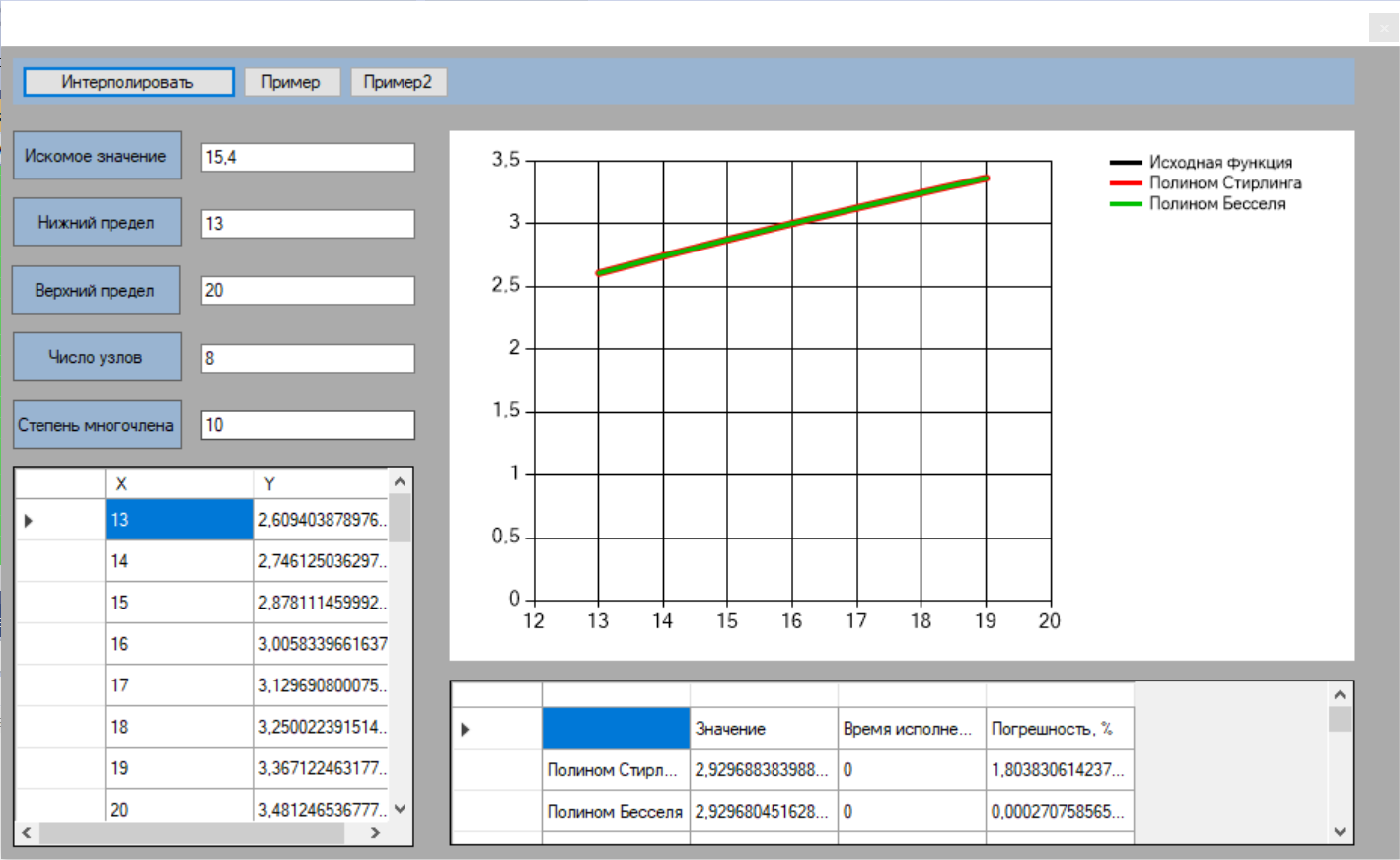 Рисунок 3 – Результат программы со степенью десять 7. ПРОВЕРКА КОРРЕКТНОСТИ РАБОТЫ ПРОГРАММЫМы должны проверить корректность работоспособности программы. Для этого мы, используя формулы подставляем наши значения, получаем ответ и сравниваем его с ответом программы. Начнем с полинома Стирлинга. Формула Стирлинга (4). Возьмем точку X= 4,3 с диапазоном от 0 до 7 с шагом 1, тогда 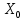 = 4 ,поскольку 4,3 ближе к 4. Посчитаем коэффициент t: = 4 ,поскольку 4,3 ближе к 4. Посчитаем коэффициент t: 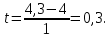 Затем построим конечную разность функции. Конечная разность представлена на таблице 1: Таблица 1 – Конечная разность
Мы построили конечные разности для многочлена третьей степени, степени относительно 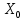 . Теперь посчитаем значение в точке: . Теперь посчитаем значение в точке: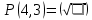 Результат, получившийся ручным путём, хоть и имеет не большую погрешность и является сходным с программным. Программа работает корректно. Теперь надо проверить следующий полином, полином Бесселя. У нас уже есть посчитанный коэффициент t=0.3 и посчитанная конечная разность в таблице 1. Теперь мы можем сразу в формулу (5) подставить наши значения и выяснить корректность роботы полинома Бесселя. Считаем значение в точке: 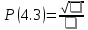 Результат, получившийся ручным путём, хоть и имеет не большую погрешность и является сходным с программным. Программа работает корректно. 8. СРАВНИТЕЛЬНЫЙ АНАЛИЗ ИНТЕРПОЛЯЦИОННЫХ МНОГОЧЛЕНОВДля сравнительного анализа проведем эксперимент. За исходные данные возьмем 3 варианта: с малой степенью, со средней и высокой. В процессе будем засекать время работы программы, без операции ввода исходных данных. Результаты сравнительного анализа сведем в таблицу 2. Таблица 2 – Сравнительный анализ
Исходя из наших выводов, эти два полинома считает почти одинаково, но в интерполировании с помощью полинома Стирлинга больше погрешность, так как выбранная точка находится ближе к середине узлов 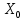 и и 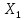 при этом при увеличении степени многочлена существенно точность не меняется. При большинстве значений разность не существенная, как можно видеть из рисунков 1-3. Также из графиков функции видно, что многочлены накладываются друг на друга, что также говорит о универсальности обоих многочленов. при этом при увеличении степени многочлена существенно точность не меняется. При большинстве значений разность не существенная, как можно видеть из рисунков 1-3. Также из графиков функции видно, что многочлены накладываются друг на друга, что также говорит о универсальности обоих многочленов. ЗАКЛЮЧЕНИЕВ ходе курсовой работы мной были закреплены теоретические знания по курсу «Численные методы» и получены практические навыки построения интерполяционного многочлена с заданными характеристиками. В ходе выполнения данной работы были подробно изучены два интерполяционных многочлена, Стирлинга и Бесселя. Было реализовано программное обеспечение на языке высокого уровня С# с использованием интегрированной среды разработки программ MS Visual Studio 2019. для интерполяции функции, заданной таблично. БИБЛИОГРАФИЧЕСКИЙ СПИСОКПолное руководство по языку программирования С#. [Электронный ресурс] - URL: https://metanit.com/ (дата обращения 06.05.2022). Уроки программирования с нуля. [Электронный ресурс] - URL: http://mycsharp.ru/ (дата обращения 09.052022). C Sharp [Электронный ресурс] - URL: https://ru.wikipedia.org/ (дата обращения 12.05.2022). Программирование, NET: [Электронный ресурс] - URL: https://habr.com/ (дата обращения 15.05.2022). Документация по C# [Электронный ресурс] - URL: https://docs.microsoft.com/ (дата обращения 22.05.2022). Справочник - А.А. Гусак, В.М. Гусак [Электронный ресурс] – URL: https://matica.org.ua/metodichki-i-knigi-po-matematike/spravochnik-a-a-gusak-v-m-gusak (дата обращения 29.05.2022) ГОСТ 28397-89 Языки программирования. Термины и определения. ГОСТ 19.504 – 79 Руководство программиста. Требования к содержанию и оформлению. ГОСТ 19.404 – 79 Единая система программной документации. Пояснительная записка. Требования к содержанию и оформлению ПРИЛОЖЕНИЕ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||