|
Рамки. 2201-5353_Рамки. Пояснительная записка 37 с., 9 рис., 10 источников
 1 Измерение расхода методом переменного перепада давлений 1 Измерение расхода методом переменного перепада давлений
Принцип действия расходомеров данного типа, объединенных единым методом измерений, основан на измерении перепада давления, образующегося в результате местного изменения скорости потока жидкости, газа или пара.
Метод переменного перепада давления один из наиболее старых и изученных методов измерения расхода. Это, а также возможность косвенной градуировки и поверки стандартизованных первичных преобразователей — сужающих устройств, реализующих метод, их простота и надежность, серийный выпуск вторичных преобразователей — дифманометров обусловило его чрезвычайно широкое (преимущественное по сравнению с другими) использование в практике промышленных измерений расхода. И вместе с тем в основе этого чисто гидродинамического метода лежат столь сложные физические процессы деформации потоков, столь большое число неконтролируемых факторов влияет на характер этих процессов, что применение его в настоящее время ограничено областями, где требуется относительно низкая точность измерений, хотя возможности его «метрологического совершенствования» далеко не исчерпаны.
Рассмотрим идеальную физическую картину явлений, лежащих в основе метода измерения расхода по перепаду давления на сужающем устройстве.
На рисунке 1.1, а приведена идеализированная картина потока, протекающего в трубопроводе 1 через сужающее устройство 2 типа «диафрагма», а также графики распределения давления (рисунок 1.1, б) и скорости (рисунок 1.1, в).
Выделим в трубопроводе три сечения: А-А — перед сужающим устройством, где еще нет его влияния на поток; В-В — место наибольшего сужения струи; С-С— сечение после сужающего устройства, где устанавливаются скорость и давление потока.
Изменение давления струи по оси трубопровода практически совпадает с изменением давления около его стенки, за исключением участка перед диафрагмой и непосредственно в ней. Однако если скорость потока W3в сечении С-С в идеальном случае равна скорости Wдо сужения, т. е. в сечении А-А, то давление Р’3в сечении С-С не достигает прежнего значения на величину 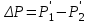 , называемую безвозвратной потерей давления. Эта потеря давления связана с затратой части энергии потока на вихреобразования в мертвых зонах (в основном за диафрагмой) и на трение. , называемую безвозвратной потерей давления. Эта потеря давления связана с затратой части энергии потока на вихреобразования в мертвых зонах (в основном за диафрагмой) и на трение.
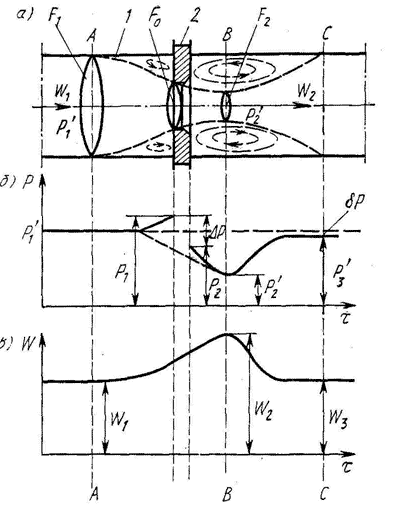
Рисунок 1.1 – Картина течения вещества через диафрагму (а) и эпюры давления (б) и скорости(в)
 Выведем уравнение расхода для несжимаемой жидкости, протекающей через диафрагму. При этом примем следующие предпосылки: движение жидкости установившееся, поток однороден и его фазовое состояние не меняется при прохождении через диафрагму, поток полностью заполняет все сечение трубопровода до и после сужающего устройства, отсутствуют возмущения потока, а прямые участки трубопровода достаточно велики. Выведем уравнение расхода для несжимаемой жидкости, протекающей через диафрагму. При этом примем следующие предпосылки: движение жидкости установившееся, поток однороден и его фазовое состояние не меняется при прохождении через диафрагму, поток полностью заполняет все сечение трубопровода до и после сужающего устройства, отсутствуют возмущения потока, а прямые участки трубопровода достаточно велики.
Для горизонтального участка трубопровода уравнение энергии потока несжимаемой жидкости для сечений А-А и В-В (рисунок 1.1) будет
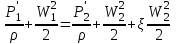 , (1.1) , (1.1)
где 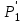 и и 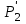 — абсолютные статические давления соответственно в сечениях А-А и В-В; — абсолютные статические давления соответственно в сечениях А-А и В-В;
W1и W2— скорости потока соответственно в сечениях А-А и В-В;
ρ — плотность жидкости;
ξ — коэффициент гидравлических потерь;
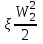 — потеря энергии на трение на участке А-А—В-В. — потеря энергии на трение на участке А-А—В-В.
Согласно уравнению неразрывности струи
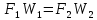 (1.2) (1.2)
 где F1и F2 — площади поперечного сечения потока соответственно в сечениях А-А и В-В. где F1и F2 — площади поперечного сечения потока соответственно в сечениях А-А и В-В.
Введем следующие обозначения:
F0/F1 =d 2/D 2=m, (1.3)
F2/F0 = μ, (1.4)
где F0и d— площадь и диаметр входного отверстия сужающего устройства;
D— диаметр трубопровода;
т — относительная площадь (модуль) сужающего устройства ;
μ — коэффициент сужения струи.
Из уравнения (1.2) и выражений (1.3) и (1.4) имеем
W1= μmW2(1.5)
Подставляя это значение W1в уравнение (1.2), определим скорость потока в месте наибольшего сужения:
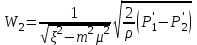 (1.6) (1.6)
Обычно перепад давления измеряют не в сечениях А-А и В-В (т. е. не 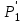 — —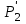 ), а непосредственно до и после сужающего устройства, а именно ), а непосредственно до и после сужающего устройства, а именно 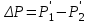 . Соотношение между указанными перепадами устанавливается с помощью поправочного коэффициента ψ, т. е. . Соотношение между указанными перепадами устанавливается с помощью поправочного коэффициента ψ, т. е.
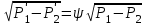 (1.7) (1.7)
Тогда уравнение (1.6) примет вид
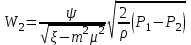 (1.8) (1.8)
Массовый расход вещества
G = W2F2ρ = W2 μF0ρ
Подставляя сюда F2 из выражения (1.8), получим
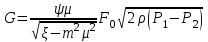 (1.9) (1.9)
Коэффициенты μ и ψ не могут быть определены независимо друг от друга. Исходя из этого, их объединяют в один экспериментально определяемый комплексный коэффициент 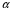 , называемый коэффициентом расхода: , называемый коэффициентом расхода:
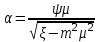 (1.10) (1.10)
Таким образом, учитывая выражения (1.9) и (1.10) и принимая во внимание, что F0 = πd2/4, получим уравнения для массового G и объемного Q расходов несжимаемой жидкости:
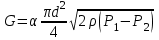 (1.11) (1.11)
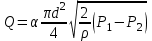 (1.12) (1.12)
Если через сужающее устройство протекает сжимаемая среда (газ или пар), то вследствие понижения давления увеличивается ее объем. Это приводит к тому, что скорость потока возрастает и становится больше скорости несжимаемой среды. В результате на сужающем устройстве увеличивается перепад давления.
Учет указанного явления производится введением в уравнения расходов (1.11) и (1.12) дополнительного коэффициента ε < 1, называемого поправочным множителем на расширение измеряемой среды.
Тогда уравнения для массового G и объемного Q расходов сжимаемой среды запишем в виде:
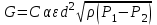 (1.13) (1.13)
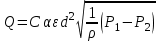 (1.14) (1.14)
где 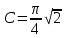 — постоянный коэффициент; — постоянный коэффициент;
ρ — плотность среды в рабочих условиях на входе в сужающее устройство, т. е. при давлении P1 и температуре T1перед сужающим устройством.
Уравнения (1.13) и (1.14) являются основными уравнениями расхода как для сжимаемых, так и несжимаемых сред, при этом для последних ε = 1. Использование уравнений (1.13) и (1.14) возможно только при условии, что скорость газа или пара меньше критической скорости.
|
|
|
 Скачать 0.76 Mb.
Скачать 0.76 Mb.