Рамки. 2201-5353_Рамки. Пояснительная записка 37 с., 9 рис., 10 источников
 Скачать 0.76 Mb. Скачать 0.76 Mb.
|
2.2 Оценка погрешности косвенных измеренийНаиболее часто используют классификацию видов измерений по способу получения числового значения измеряемой величины. В этом случае все измерения делят на четыре основных вида: – прямые измерения; – косвенные измерения; – совокупные измерения; – совместные измерения Косвенными называют измерения, результат которых определяют на основе прямых измерений величин, связанных с измеряемой величиной известной зависимостью 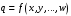 , где , где 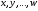 – результаты прямых измерений, – результаты прямых измерений, 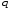 – измеряемая величина. – измеряемая величина. Находить значения некоторых величин легче и проще путем косвенных измерений, чем путем прямых. Иногда прямые измерения невозможно осуществить. Нельзя, например, измерить плотность твердого тела, определяемую обычно по результатам измерений объема и массы. Косвенные измерения некоторых величин позволяют получить значительно более точные результаты, чем прямые. Находить значения некоторых величин легче и проще путем косвенных измерений, чем путем прямых. Иногда прямые измерения невозможно осуществить. Нельзя, например, измерить плотность твердого тела, определяемую обычно по результатам измерений объема и массы. Косвенные измерения некоторых величин позволяют получить значительно более точные результаты, чем прямые.Специфической особенностью косвенных измерений являются одновременные прямые измерения значений аргументов, что позволяет подставить полученные значения аргументов в зависимость 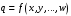 и рассчитать значение измеряемой величины, отвечающее моменту времени измерения аргументов. Измеряя значения аргументов, результат всегда получают с некоторой определенной погрешностью, зависящей от метода измерения соответствующего аргумента и используемых СИ. Эта погрешность всегда может быть оценена. и рассчитать значение измеряемой величины, отвечающее моменту времени измерения аргументов. Измеряя значения аргументов, результат всегда получают с некоторой определенной погрешностью, зависящей от метода измерения соответствующего аргумента и используемых СИ. Эта погрешность всегда может быть оценена. Погрешность результата q также будет функционально связана с погрешностями измеряемых величин х, у, …, w. Значения х, у, …, w обычно находят путем прямых измерений, и их погрешности определяются чаще всего пределами допускаемых погрешностей применяемых средств измерений. Систематические погрешности полагают исключенными путем введения поправок. Иногда погрешности измерений аргументов бывают заданы не их границами, а характеристиками составляющих: среднеквадратическим отклонением (СКО) случайной погрешности и доверительными границами неисключенной систематической погрешности. В зависимости от применяемых методов и средств измерений, а также от условий, в которых производятся измерения величин х, у, …, w, значения их погрешностей могут быть независимы или коррелированы между собой. Погрешность результата q также будет функционально связана с погрешностями измеряемых величин х, у, …, w. Значения х, у, …, w обычно находят путем прямых измерений, и их погрешности определяются чаще всего пределами допускаемых погрешностей применяемых средств измерений. Систематические погрешности полагают исключенными путем введения поправок. Иногда погрешности измерений аргументов бывают заданы не их границами, а характеристиками составляющих: среднеквадратическим отклонением (СКО) случайной погрешности и доверительными границами неисключенной систематической погрешности. В зависимости от применяемых методов и средств измерений, а также от условий, в которых производятся измерения величин х, у, …, w, значения их погрешностей могут быть независимы или коррелированы между собой.Для нахождения погрешности результата косвенного измерения можно воспользоваться следующими правилами: 1. Если окончательный результат измерения выражается суммой или разностью двух или более измеренных значений: 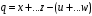 , (2.6) , (2.6)погрешности ∆x, …, ∆w независимы и случайны, то абсолютная погрешность результата может быть найдена по формуле: 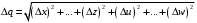 , (2.7) , (2.7)Когда погрешности аргументов коррелированы, значение ∆q может превышать полученное по приведенной выше формуле, но всегда удовлетворяет условию 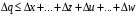 (2.8) (2.8)2. Если окончательный результат измерения выражается произведением или частным двух или более измеренных значений: 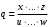 , (2.9) , (2.9)погрешности 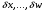 независимы и случайны, то относительная погрешность результата может быть найдена по формуле независимы и случайны, то относительная погрешность результата может быть найдена по формуле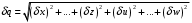 , (2.10) , (2.10)Когда погрешности аргументов коррелированы, значение 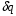 может превышать полученное по приведенной формуле, но всегда удовлетворяет условию может превышать полученное по приведенной формуле, но всегда удовлетворяет условию 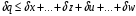 , (2.11) , (2.11)3. Если окончательный результат измерения является функцией одной величины: 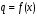 , (2.11) , (2.11)то погрешность результата составляет 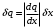 , (2. 12) , (2. 12) 4. В общем случае погрешность функции нескольких величин 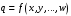 , погрешности которых независимы и случайны, находится по формуле: , погрешности которых независимы и случайны, находится по формуле: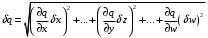 (2.13) (2.13)В любом случае погрешность никогда не превышает значения 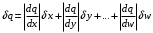 (2.14) (2.14)Из уравнений расхода (1.13) и (1.14) следует, что значение расхода является результатом косвенных измерений. Поэтому погрешность измерения расхода может быть определена в соответствии с выражением (2.13), если известны погрешности измерения величин, входящих в уравнения расхода. Так, среднеквадратическую погрешность измерения массового расхода 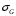 можно определить по известным среднеквадратическим погрешностям можно определить по известным среднеквадратическим погрешностям 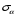 , , 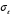 , , 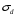 , , 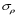 , , 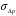 , при отсутствии корреляционной зависимости между ними, получаем: , при отсутствии корреляционной зависимости между ними, получаем: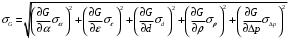 (2.15) (2.15) Уравнение расхода содержит две группы величин, различающихся способом получения их значений. К первой группе относятся Уравнение расхода содержит две группы величин, различающихся способом получения их значений. К первой группе относятся 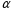 и и 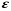 , значения которых найдены в результате обработки большого числа измерений и для которых известны среднеквадратические погрешности , значения которых найдены в результате обработки большого числа измерений и для которых известны среднеквадратические погрешности 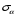 и и 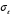 . Ко второй группе величин относятся . Ко второй группе величин относятся 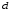 , , 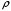 и и 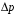 , которые определяются по результатам однократных измерений и для которых по метрологическим характеристикам средств измерений могут быть определены только предельные значения погрешностей. Для возможности использования (2.13) принимается, что для второй группы величин среднеквадратическая погрешность измерений с вероятностью 0,95 равна половине максимальной (предельной), тогда , которые определяются по результатам однократных измерений и для которых по метрологическим характеристикам средств измерений могут быть определены только предельные значения погрешностей. Для возможности использования (2.13) принимается, что для второй группы величин среднеквадратическая погрешность измерений с вероятностью 0,95 равна половине максимальной (предельной), тогда 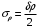 , , 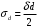 , , 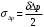 . Обычно, дифманометры снабжены устройствами для извлечения квадратного корня из измеряемого перепада . Обычно, дифманометры снабжены устройствами для извлечения квадратного корня из измеряемого перепада 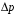 для получения равномерной по расходу шкалы. В этом случае класс дифманометра характеризует точности измерений для получения равномерной по расходу шкалы. В этом случае класс дифманометра характеризует точности измерений 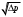 , а не , а не 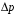 . Вычисляя производные в (2.15), получаем: . Вычисляя производные в (2.15), получаем: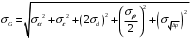 (2.16) (2.16)При изготовлении сужающих устройств принимается очень малые значения допусков на диаметр отверстия 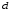 . Окончательно, получим: . Окончательно, получим: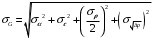 (2.17) (2.17) |
