|
Рамки. 2201-5353_Рамки. Пояснительная записка 37 с., 9 рис., 10 источников
 3 Расчет расходомера с СУ 3 Расчет расходомера с СУ
Исходные данные:
– Измеряемая среда –воздух.
– Расход – 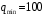 м3/ч, м3/ч, 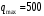 м3/ч м3/ч
– Диаметр трубопровода – наружный 108 мм, толщина стенки 4 мм.
– Вид СУ—ИСА 1932.
– Перепад давлений на СУ – 10000 Па.
– Максимальная потеря давления на СУ –…. кПа.
– Рабочая температура – 50 оС.
– Рабочее давление (избыт) – 0.4 МПа.
– Влажность среды – 75%.
– Материал трубопровода—Ст35.
– Материал СУ—40Х.
Местные сопротивления до СУ – шаровый кран.
3.1 Расчет диаметра отверстия СУ
Массовый расход через СУ определяется по следующей формуле (5.1) ГОСТ 8.586.1—2005:
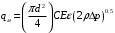 , (3.1) , (3.1)
Примем коэффициент расхода 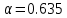 .Так как воздух—сжимаемая среда, .Так как воздух—сжимаемая среда, 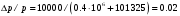 (мало), то коэффициент сжатия примем (мало), то коэффициент сжатия примем 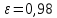 . Плотность воздуха при температуре 50 . Плотность воздуха при температуре 50 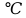 по [10] равна 1,093 кг/м3. по [10] равна 1,093 кг/м3.
Из формулы (3.1) выразим неизвестный диаметр сопла d:
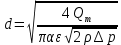 (3.2) (3.2)
Подставляя заданные и принятые величины, найдем значение d:
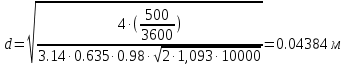 . .
Определим относительный диаметр 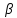 по формуле (3.1) ГОСТ 8.586.1: по формуле (3.1) ГОСТ 8.586.1:
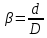 , (3.3) , (3.3)
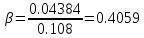 . .
Проверим правильность нахождения 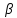 . .
По уравнению (5.9) ГОСТ 8.586.1 определим число Рейнольдса:
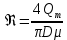 , (3.4) , (3.4)
Коэффициент динамической вязкости воздуха при температуре 50 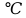 по [10] равен 19,1 по [10] равен 19,1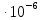 Па Па с. с.
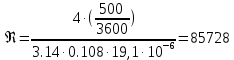 . .
Сопла ИСА 1932 применяют при 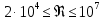 и и 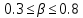 . .
 Рассчитаем вспомогательную величину Рассчитаем вспомогательную величину
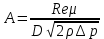 , (3.5) , (3.5)
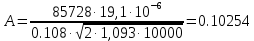
Относительно неизвестной величины 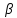 решим следующее уравнение ((В.17) ГОСТ 8.586.1): решим следующее уравнение ((В.17) ГОСТ 8.586.1):
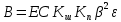 , (3.6) , (3.6)
Решение уравнения (3.6) может быть выполнено любым итерационным методом. При применении метода бисекции решение уравнения выполняют в следующей последовательности:
– рассчитывают значение
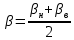 , (3.7) , (3.7)
где 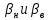 — верхнее и нижнее значение — верхнее и нижнее значение 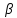 соответственно из допустимого диапазона. В качестве соответственно из допустимого диапазона. В качестве 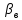 возьмем значение возьмем значение 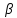 , рассчитанное по (3.3) , рассчитанное по (3.3)
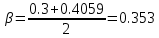
Коэффициент истечения С находим по формуле (5.6) ГОСТ 8.586.2:
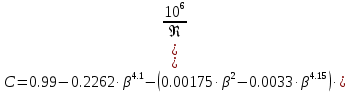 (3.8) (3.8)
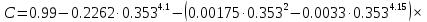
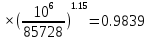
Коэффициент скорости выхода Е рассчитываем по 3.3.10 ГОСТ 8.586.1:
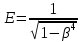 , (3.9) , (3.9)
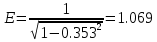
Коэффициенты Кш и Кп принимаем равными 1.
Рассчитываем В:
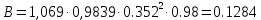 . .
 – проверяем выполнение неравенства (В.20) ГОСТ 8.586.1: – проверяем выполнение неравенства (В.20) ГОСТ 8.586.1:
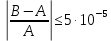 , (3.10) , (3.10)
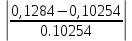 =0.25 =0.25
Так как неравенство (3.10) не выполняется, рассчитываем новое значение 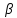 по формуле (3.7), в которой принимаем по формуле (3.7), в которой принимаем 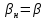 , рассчитанное на первом шаге итерации. Для нового значения , рассчитанное на первом шаге итерации. Для нового значения 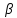 рассчитываем В по (3.5) и проверяем выполнение неравенства (3.10). рассчитываем В по (3.5) и проверяем выполнение неравенства (3.10).
Решая дальше данные уравнения, определяем, что неравенство (3.10) будет выполняться при 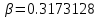 . .
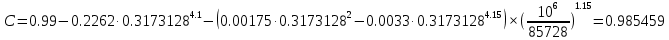
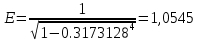 , ,
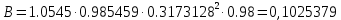 . .
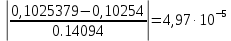 . .
Так как неравенство (3.9) выполняется, то значение 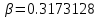 принимаем как окончательное. принимаем как окончательное.
В соответствии с найденным значением 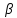 пересчитаем значение пересчитаем значение 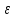 по формуле (А.14) ГОСТ 8.586.1: по формуле (А.14) ГОСТ 8.586.1:
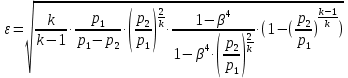 , (3.11) , (3.11)
где k— показатель адиабаты. По таблице 6 [3] для воздуха k=1.4,
р1—давление среды в ИТ до СУ, р2—давление среды в ИТ после СУ.
р1=ра+ри . (3.12)
р2=р1-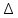 р. (3.13) р. (3.13)
р1=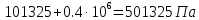
р2=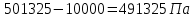
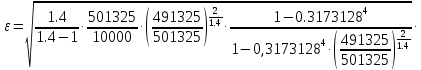
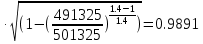
Коэффициент расхода
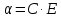 (3.14) (3.14)
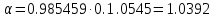
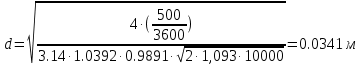 . .
После этого произведем проверку расчета путем подстановки всех найденных величин в правую часть уравнения (3.1):
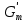 = =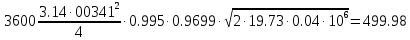 кг/с кг/с
Определим относительную погрешность вычислений:
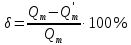 . (3.15) . (3.15)
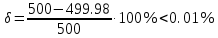
 Так как Так как 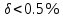 расчеты можно считать верными. расчеты можно считать верными.
|
|
|
 Скачать 0.76 Mb.
Скачать 0.76 Mb.