Рамки. 2201-5353_Рамки. Пояснительная записка 37 с., 9 рис., 10 источников

• Название: Пояснительная записка 37 с., 9 рис., 10 источников
• Анкор: Рамки
• Дата: 30.04.2022
• Размер: 0.76 Mb.
• Имя файла: 2201-5353_Рамки.docx
• Тип: Пояснительная записка; #505697
• страница: 6 из 10

2.3. Неопределенности измерений

Неопределенность измерений – это характеристика недостоверности измерений, принятая на международном уровне [3].

Понятие «неопределенность» произошло от английского слова «uncertainty». Неопределенность отражает отсутствие точного знания (истинного) значения измеряемой величины Y и выражает сомнение в том, насколько точно результат измерения у представляет Y. В соответствии с определением, неопределенность – это параметр, связанный с результатом измерений у и характеризующий разброс значений, которые можно обоснованно приписать измеряемой величине Y. Первая буква слова «uncertainty» 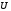стала обозначением этого параметра. Приведенное определение лучше всего иллюстрируется стандартной формой записи результата измерения 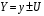, 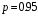. Из выражения видно, что вероятный разброс значений Y находится в диапазоне ±U относительно результата измерения у (рисунок 2.1), а степень обоснованности нахождения значений Y в этом интервале определяется вероятностью (уровнем доверия) .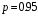



Рисунок 2.1 – Определение неопределенности измерения
По источнику возникновения неопределенности измерений, подобно погрешностям, можно разделять на инструментальные, методические и субъективные.

По характеру проявления погрешности разделяют на систематические, случайные и грубые. В «Руководстве по выражению неопределенности измерения» отсутствует классификация неопределенностей по этому признаку. В самом начале этого документа указано, что перед статистической обработкой рядов измерений все известные систематические погрешности должны быть из них исключены. Поэтому деление неопределенностей на систематические и случайные не вводилось. Вместо него приведено деление неопределенностей по способу оценивания на два типа:

– неопределенность, оцениваемая по типу А (неопределенность типа А) – неопределенность, которую оценивают статистическими методами,

– неопределенность, оцениваемая по типу Б (неопределенность типа Б) – неопределенность, которую оценивают не статистическими методами.

Соответственно предлагается и два метода оценивания:

–оценивание по типу А — получение статистических оценок на основе результатов ряда измерений,

–оценивание по типу Б — получение оценок на основе априорной нестатистической информации.

Составляющие типа А оцениваются как стандартные неопределенности ( 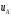), равные среднеквадратическим отклонениям (СКО) средних арифметических многократных наблюдений.

Составляющие типа В ( 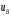) оцениваются как стандартные (среднеквадратические) отклонения, получаемые из известных границ, в которых могут находиться значения измеряемых величин.

Все составляющие формируют суммарную стандартную неопределенность 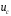, которая вычисляется по правилу суммирования дисперсий: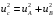

(2.18)

откуда путем извлечения корня из обеих частей равенства, получа­м выражение, называемое законом распространения неопределенности: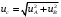

(2.19)

Интервальной оценкой неопределенности является расширенная неопределенность U, которую получают путем умножения стандартной суммарной неопределенности 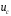на коэффициент охвата :

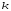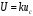(2.20)

В общем случае коэффициент охвата находят как коэффициент Стьюдента для вероятности 0,95.

Схожесть понятий «погрешность измерений» и «неопределенность измерений» трактуется в [4].

Погрешность измерения (error of measurement): Результат измерения (измеренное значение величины) минус опорное значение величины (опорное значение величины (reference quantity value) – значение величины, используемое как основа для сравнения со значением величины того же рода).

Примечание 1 – Понятие «погрешность измерения» может быть использовано двояко:

a) когда имеется единственное опорное значение величины, которое появляется при выполнении калибровки посредством эталона с регламентированным значением величины, имеющим незначительную неопределенность измерения, или если дано приписанное (стандартизованное) значение величины; в таком случае погрешность измерения известна, и

b) если измеряемая величина предполагается представленной однозначно определенным истинным значением или рядом истинных значений величины незначительного размаха; в таком случае погрешность измерения неизвестна.

Неопределенность измерения (uncertainty of measurement): Неотрицательный параметр, характеризующий разброс значений величины, приписываемых измеряемой величине на основе используемой информации.

Примечание 1 – Неопределенность измерения включает в себя составляющие, обусловленные систематическими эффектами, такие как составляющие, связанные с поправками и приписанными эталонам значениями величин, а также с неопределенностью определения (измеряемой величины). Иногда оцененные систематические эффекты не исключают из связанных с ними составляющих неопределенности измерений.

Примечание 2 – Параметр может быть, например, стандартным отклонением, называемым стандартной неопределенностью измерения (или заданным кратным ей), или половиной ширины интервала, имеющего установленную вероятность охвата.

Примечание 3 – В общем случае неопределенность измерения содержит много составляющих. Некоторые из этих составляющих могут быть оценены по типу А оценки неопределенности измерения из статистического распределения значений величины в серии измерений и охарактеризованы стандартным отклонением.

Другие составляющие, которые могут быть оценены по типу В оценки неопределенности измерения, могут также быть охарактеризованы стандартным отклонением, оцененным из функций плотности вероятности, основанных на опыте или другой информации.

Примечание 4 – В общем случае подразумевается, что неопределенность измерения связана с определенным значением, приписанным измеряемой величине. С изменением этого значения изменяется соответствующая неопределенность.

Согласно данному документу, можно предложить общее правило: результаты измерений в большинстве метрологических ситуаций характеризуются неопределенностью, а нормативы точности средств измерений, измерительных и контрольных процедур характеризуются погрешностью. Таким образом, понятия «неопределенность» и «погрешность» рекомендуется гармонично использовать без взаимного противопоставления и исключения одного из них.

Для определения неопределенности можно использовать такую характеристику прибора, как класс точности. Этапы расчета:

1. Вычисление среднего арифметического значение параметра из всех измерений в данной точке: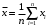

(2.21)

2. Для источников неопределенности случайного характера вычисляем неопределенность по типу А: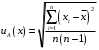

(2.22)

3. Для источников неопределенности систематического характера (приборная погрешность) вычисляем неопределенность по типу Б: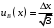

(2.23)

где ± 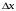– пределы допускаемой приборной погрешности.

4. Вычисляем суммарную стандартную неопределенность: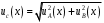



5. Для доверительной вероятности (вероятности охвата) р = 0.95 (рекомендуется в Руководстве по расчету неопределенности) задаем коэффициент охвата k = 2 и вычисляем расширенную неопределенность измерений: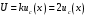