курсовой метрология. Пояснительная записка 38 листов, табл. 5, библиографический список 5 наименований
 Скачать 121.1 Kb. Скачать 121.1 Kb.
|
Задание 2. Определение значения погрешности измеренияПри измерении напряжение показания вольтметра 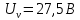 . Поправка к показаниям прибора . Поправка к показаниям прибора 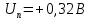 . Определить значение погрешности измерения и погрешности средства измерений (вольтметра), если действительное значение напряжения . Определить значение погрешности измерения и погрешности средства измерений (вольтметра), если действительное значение напряжения 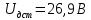 . .Ход решения. Определим погрешность средства измерения-вольтметра, которая находиться по формуле (4): 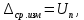 (4) (4)где 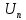 – поправка к показаниям прибора, В; – поправка к показаниям прибора, В;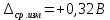 . .Определим измеряемую величину по формуле (5): 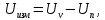 (5) (5)где 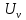 – показания прибора, В; – показания прибора, В;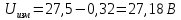 . .Определим абсолютную погрешность, подставив полученные данные в формулу (6): 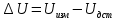 , (6) , (6)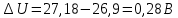 . .Определим относительную погрешность измерения, подставив полученные данные в формулу (7): 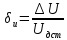 , (7) , (7)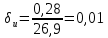 . .Задание 3. Разность результата измерения и истинного значенияСлучайная погрешность измерения напряжения распределена по нормальному закону. При обработке результатов измерений получены следующие оценки погрешностей: систематическая погрешность 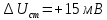 ; оценка ; оценка 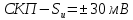 . Определить вероятность того, что результат измерения отличается от истинного значения не более чем на . Определить вероятность того, что результат измерения отличается от истинного значения не более чем на 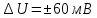 , при условии, что поправка на систематическую погрешность не вводится. , при условии, что поправка на систематическую погрешность не вводится.Ход решения. Для оценки результатов измерений, содержащих случайные погрешности, пользуются понятиями и методами теории вероятностей и математической статистики, поскольку закономерности в появлении этих значений нет. Результат отдельного наблюдения при многократном прямом измерении какой-либо физической величины из-за наличия случайных погрешностей представляет собой случайную величину. Вероятность событияявляется количественной оценкой объективной возможности его появления. Вероятность достоверного события равна единице, а вероятность невозможного события – нулю. События, вероятности появления которых больше нуля и меньше единицы, являются событиями случайными. Применительно к области измерений можно считать, что при проведении равноточных наблюдений каждая из множества возможных незначительных причин случайных изменений результатов может появиться или не появиться. В итоге случайные измерения, появляющиеся при каждом измерении, могут быть любыми как по размеру, так и по знаку. Наличие систематической погрешности делает интервал несимметричным относительно нуля. В этом случае доверительная вероятность определяется по формуле (8). 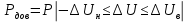 , (8) , (8)Нижнюю границу доверительного интервала найдем по формуле 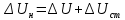 (9) (9)Верхнюю границу доверительного интервала найдем по формуле 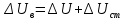 (10) (10)Определим нормированные границы доверительного интервала по формуле (11): 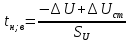 (11) (11)где 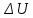 – отличие от истинного значения; – отличие от истинного значения;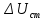 – систематическая погрешность; – систематическая погрешность;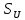 – оценка СКП; – оценка СКП;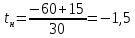 . .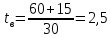 . .Значение нормированной интегральной функции нормального распределения определяем по таблице значений функции стандартного нормального закона распределения. Для определения доверительной вероятности в случае несимметричного интервала воспользуемся формулой (12). 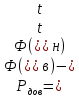 , (12) , (12)где 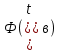 – верхнее значение интегральной функции нормального распределения; – верхнее значение интегральной функции нормального распределения;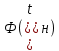 – нижнее значение интегральной функции нормального распределения; – нижнее значение интегральной функции нормального распределения;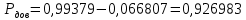 . .Таким образом доверительная вероятность при 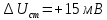 будет равна формуле (8). будет равна формуле (8).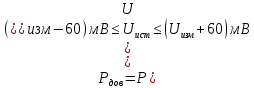 . . |
