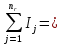курсовой метрология. Пояснительная записка 38 листов, табл. 5, библиографический список 5 наименований
 Скачать 121.1 Kb. Скачать 121.1 Kb.
|
Значения  (графа 4 таблица 5) рассчитаны путем использования значений функции стандартного нормального закона распределения по таблице П3.3 приложение 3 [2] (с учетом нормализованной функции экспериментального распределения) по формуле (23) (графа 4 таблица 5) рассчитаны путем использования значений функции стандартного нормального закона распределения по таблице П3.3 приложение 3 [2] (с учетом нормализованной функции экспериментального распределения) по формуле (23)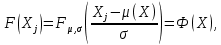 (23) (23)где 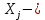 результат j-го наблюдения случайной величины результат j-го наблюдения случайной величины 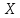 ; ;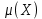 – математическое ожидание случайной величины – математическое ожидание случайной величины 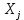 ; ;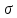 – дисперсия случайной величины – дисперсия случайной величины 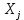 ; ;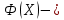 значение функции стандартного нормального закона распределения при значение функции стандартного нормального закона распределения при 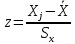 . .Лучшей оценкой 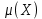 является среднее арифметическое является среднее арифметическое 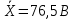 результатов наблюдений, а лучшей оценкой результатов наблюдений, а лучшей оценкой  является выборочное стандартное отклонение является выборочное стандартное отклонение 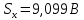 (среднее квадратическое отклонение) результатов наблюдений. (среднее квадратическое отклонение) результатов наблюдений.В этом случае значение функци нормального распределения по экспериментальным данным для j-го результата наблюдений будет определяться по таблице П3.3 приложение 3 [2] по выражению 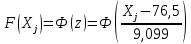 , (24) , (24)Значение величины 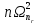 находим путем подстановки суммы результатов по графе 11 таблицы 5 в формулу (25) находим путем подстановки суммы результатов по графе 11 таблицы 5 в формулу (25)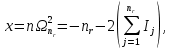 (25) (25)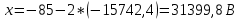 . .По таблице П3.7 приложение 3 [2] находим значение функции распределения 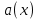 для для 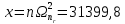 : :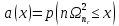 . .Так как 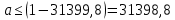 то гипотеза о соответствии эмпирического и теоретического законов распределения не принимается, т.е. экспериментально полученная совокупность результатов набледений не принадлежит нормально распределенной генеральной совокупности. то гипотеза о соответствии эмпирического и теоретического законов распределения не принимается, т.е. экспериментально полученная совокупность результатов набледений не принадлежит нормально распределенной генеральной совокупности.Стандартную неопределенность измерений 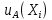 типа А входной величины типа А входной величины 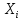 , при которой результат измерений определяют как среднее значение из повторных независимых наблюдений , при которой результат измерений определяют как среднее значение из повторных независимых наблюдений 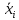 , с учетом того, что для прямых измерений с многократными наблюдениями при условии, что , с учетом того, что для прямых измерений с многократными наблюдениями при условии, что 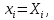 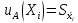 , а количество входных величин , а количество входных величин 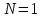 , определяем по формуле (26) , определяем по формуле (26)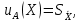 (26) (26)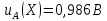 . .Число степеней свободы будет равно 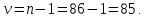 Для оценки неопределенности типа В необходимо выявить все источники систематических эффектов на основании всей имеющейся информации. Основными источниками систематических эффектов является погрешность средства измерения (основная и дополнительные погрешности) – вольтметра цифрового. Источником информации для определения границ погрешностей СИ является: метрологические характеристики СИ (таблица 2) и условия измерения: температура окружающего воздуха (среды) − 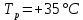 ; предел допускаемой абсолютной основной погрешности СИ ; предел допускаемой абсолютной основной погрешности СИ 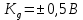 ; дополнительная погрешность в % (±) от верхнего предела измерений в зависимости от измерения влияющей величины ; дополнительная погрешность в % (±) от верхнего предела измерений в зависимости от измерения влияющей величины 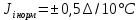 ; нормирующее значение СИ ; нормирующее значение СИ 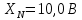 ; номинальная рабочая температура окружающего воздуха ; номинальная рабочая температура окружающего воздуха 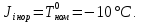 Предельная основная погрешность СИ определяем по формуле (27): 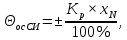 (27) (27)где 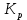 − класс точности средства измерения; − класс точности средства измерения;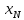 − нормирующее значение средства измерения; − нормирующее значение средства измерения;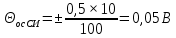 . .Границу дополнительной погрешности СИ определяем по формуле (28) 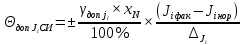 , (28) , (28)где 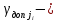 предел допускаемой приведенной дополнительной погрешности СИ в зависимости от предел допускаемой приведенной дополнительной погрешности СИ в зависимости от 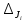 установленного интервала изменения внешней влияющей величины установленного интервала изменения внешней влияющей величины 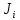 , выраженная в , выраженная в 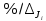 ; ;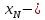 нормирующее значение СИ; нормирующее значение СИ;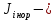 номинальное значение внешней влияющей величины; номинальное значение внешней влияющей величины;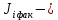 фактическое значение внешней влияющей величины; фактическое значение внешней влияющей величины;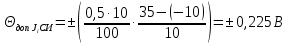 . .Вследствие отсутствия какой-либо дополнительной информации о характере распределения величин  и и  внутри указанных интервалов принимаем, что они могут принять любое значение внутри интервалов с одинаковой вероятностью, что соответствует равномерному закону распределения. Поэтому можем рассчитать неопределенности от применения СИ, как неопределенности, оцениваемые по типу В, по формуле (29) внутри указанных интервалов принимаем, что они могут принять любое значение внутри интервалов с одинаковой вероятностью, что соответствует равномерному закону распределения. Поэтому можем рассчитать неопределенности от применения СИ, как неопределенности, оцениваемые по типу В, по формуле (29)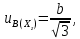 (29) (29)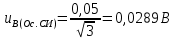 ; ;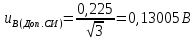 . .Суммарную стандартную неопределенность, оцененную только по типу В, рассчитываем по формуле (30): 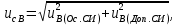 (30) (30)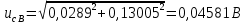 . .Для частного случая (прямые независимые многократные измерения), когда 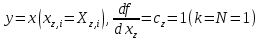 и когда измеряемая величина и когда измеряемая величина 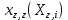 распределена по нормальному закону. Суммарную стандартную неопределенность, включающую стандартные неопределенности, оцененные по типу А, так и по типу В, рассчитываем по формуле (31): распределена по нормальному закону. Суммарную стандартную неопределенность, включающую стандартные неопределенности, оцененные по типу А, так и по типу В, рассчитываем по формуле (31):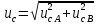 , (31) , (31)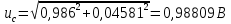 . .Расширенную неопределенность результата измерения, соответствующую интервалу с уровнем доверия примерно 95 %, определяем по формуле (32): 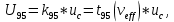 (32) (32)где 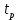 – распределение Стьюдента; – распределение Стьюдента;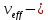 число эффективных степеней свободы число эффективных степеней свободы Для этого необходимо определить значение числа степеней свободы при получении соответствующих стандартных неопределенностей и рассчитать число эффективных степеней свободы 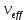 . .Число степеней свободы при определении неопределенности измерения напряжения в сети переменного тока 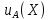 от повторных наблюдений от повторных наблюдений 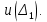 Значение давления Значение давления 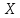 получено на основе 85 независимых повторных наблюдений, что позволяет оценить число степеней свободы для получено на основе 85 независимых повторных наблюдений, что позволяет оценить число степеней свободы для 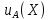 как как 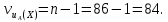 Заявленную неопределенность (относительную неопределенность), равную границам интервалов изменения погрешности СИ (основной и дополнительной), полученную на основе априорной информации, можно считать известной точно, т.е. не обладающей неопределенностью, поэтому 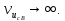 При определении неопределенности 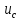 число эффективных степеней свободы может быть определено по формуле (33), которая называется формулой Уэлча-Саттертуэйта: число эффективных степеней свободы может быть определено по формуле (33), которая называется формулой Уэлча-Саттертуэйта: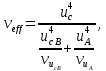 (33) (33)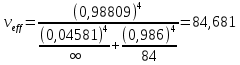 . .Из таблицы П3.6 [2] получаем 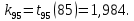 Это дает возможность рассчитать расширенную неопределенность по формуле (34) Это дает возможность рассчитать расширенную неопределенность по формуле (34)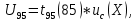 (34) (34)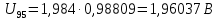 / /Измерения проводились при помощи вольтметра цифрового. Результат измерения: 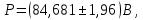 где число, стоящее после знака ( где число, стоящее после знака (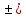 , − (расширенная неопределенность) , − (расширенная неопределенность) 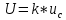 , полученная для (суммарной стандартной неопределенности и коэффициента охвата , полученная для (суммарной стандартной неопределенности и коэффициента охвата 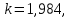 соответствующего уровню доверия соответствующего уровню доверия 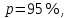 для нормального распределения, при для нормального распределения, при 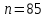 . . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||