Анализ сигналов и систем. Kursovaya_Rabota_АСИС. Пояснительная записка к курсовой работе Анализ сигналов и систем
 Скачать 1.47 Mb. Скачать 1.47 Mb.
|
Построение АЧХ и ФЧХ спектра непериодического сигналаРяд Фурье справедлив для периодических сигналов. Спектр периодического сигнала дискретен. Если сигнал непериодический, то ряд Фурье применить нельзя. Однако, непериодический сигнал (одиночный) можно представить как периодический с периодом Т→∞. Прямое преобразование Фурье: 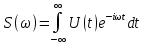 Обратное преобразование Фурье: 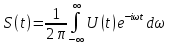 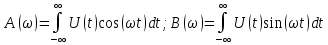 Модуль и аргумент спектральной плотности определяются выражениями: 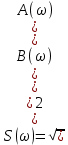 Первое из этих выражений можно рассматривать как АЧХ, а второе – как ФЧХ сплошного спектра непериодического сигнала U(t).   w, Гц U,В 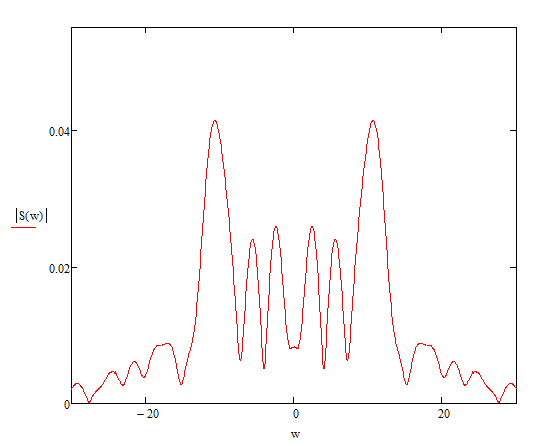 Рисунок 8 – АЧХ непериодического сигнала   w, Гц Θ, рад 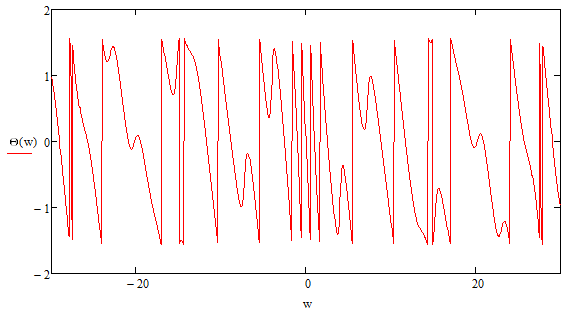 Рисунок 9 – ФЧХ непериодического сигнала Рассмотрим соотношение спектров периодического и непериодического сигналов на примере нескольких первых гармоник включая нулевую: 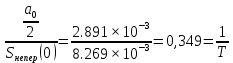 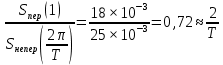 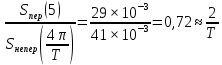 Вывод: модуль спектральной плотности одиночного импульса и огибающая линейчатого спектра периодического сигнала, полученного путём повторения заданного импульса, совпадают по форме и отличаются масштабом. Спектр периодического сигнала связан со спектром соответствующего ему непериодического сигнала соотношением: 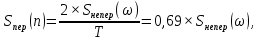 где где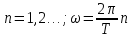   Гц U,В 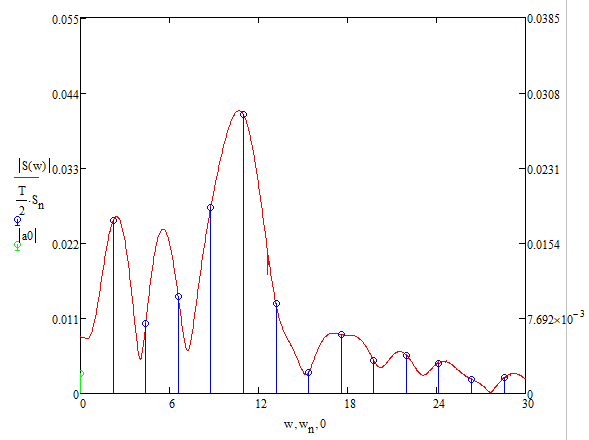 Рисунок 10 – Сравнение спектров периодического (смасштабированного в T/2 раз на ненулевых частотах и в Т раз на нулевой частоте) и непериодического сигналов   Гц Θ, рад 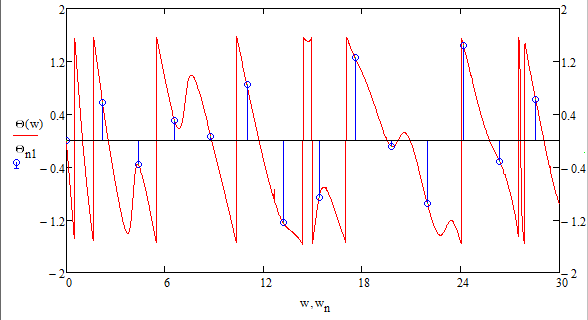 Рисунок 11 – Сравнение ФЧХ периодического и непериодического сигналов Энергия и средняя мощность периодического сигналаПусть сигнал s(t) (ток, напряжение) представляет собой сложную периодическую функцию времени с периодом Т. Энергия такого сигнала, длящегося от t=-∞ до t=∞, бесконечно велика. Основной интерес представляет средняя мощность периодического сигнала и распределение этой мощности между отдельными гармониками сигнала. Очевидно, что средняя мощность сигнала, рассматриваемого на всей оси времени, совпадает с мощностью, средней за один период Т. Таким образом, средняя мощность периодического сигнала 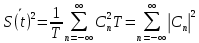 При использовании тригонометрической формы ряда Фурье, учитывая, что 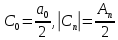 получаем получаем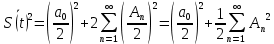 Если s(t) представляет собой ток i(t), то при прохождении его через сопротивление r выделяется мощность (средняя): 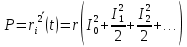 Символом 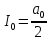 обозначена постоянная составляющая, а In =An – амплитудой n-ой гармоники тока. обозначена постоянная составляющая, а In =An – амплитудой n-ой гармоники тока.Энергия периодического сигнала за 1 период: 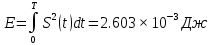 Для данного сигнала средняя мощность равна: 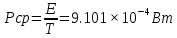 Итак, средняя мощность периодической последовательности равна сумме средних мощностей всех составляющих в спектре и не зависит от начальных фаз отдельных составляющих. |
