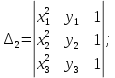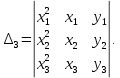Анализ сигналов и систем. Kursovaya_Rabota_АСИС. Пояснительная записка к курсовой работе Анализ сигналов и систем
 Скачать 1.47 Mb. Скачать 1.47 Mb.
|
АППРОКСИМАЦИЯ СИГНАЛАДля того, чтобы иметь возможность применить к исследованию сигнала математические методы, необходимо аппроксимировать его математической функцией, удобной для дальнейшего анализа и в то же время достаточно точно передающей форму сигнала. Для этой цели обычно используют гармонические и полиномиальные функции, а также прямые. Так как сигнал является периодическим, то его следует рассматривать на временном интервале, равном периоду сигнала. Функция разбивается на несколько участков с различным характером зависимости напряжения от времени. Выбираются участки по описанию близкие к гармонической зависимости, либо к полиномиальной зависимости. Для исследования сигнала его нужно представить в аналитической форме. После разбиения интервала, на котором представлен сигнал, на характерные участки, определяем координаты точек, соединяющих участки и координаты точек на концах интервала аппроксимации. Аппроксимирующую функцию построим из совокупности степенных функций 1-й и 2-й степени. Графики таких функций являются прямые и параболы соответственно. Для каждого участка составим уравнения прямой (или параболы), проходящей через точки – границы участка (причем, если линия является параболой, то необходимо задать координаты еще одной какой-либо точки, т.к. уравнение параболы однозначно определяется по трем точкам). Данный метод сразу позволяет получить непрерывную аппроксимирующую функцию. Уравнение прямой имеет вид y(x)=kx+b. Пусть заданы координаты двух точек (x1,y1) и (x2,у2), через которые проходит данная прямая, тогда коэффициенты k и b определятся по формулам:
Уравнение параболы имеет вид у(х) = ах2 + bx + с. Пусть заданы координаты трех точек (х1у1,), (x2,у2) и (х3,у3), через которые проходит данная парабола, тогда коэффициенты а, b и с определятся по формулам:
На рисунке 3 представлен исходный сигнал.  Рисунок 3 – исходный сигнал Выделим 12 участков аппроксимации. Определим точки сопряжения линий, координаты точек представлены в таблице 5. Воспользовавшись формулами (1-9), получим выражения для аппроксимирующей функции. Вычисления проводились с использованием программы Mathcad. Проведём аппроксимацию и построим график модели сигнала. На рисунке 4 показаны аналитические уравнения каждого из участков и их границы. Вид аппроксимированного сигнала представлен на рисунке 5. Таблица 5 - Координаты точек аппроксимации
 Рисунок 4 – Аналитические уравнения участков 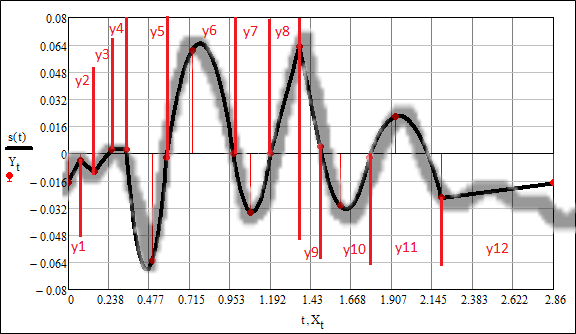 Рисунок 5 – Аппроксимированный сигнал |

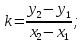
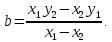
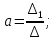
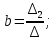
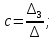
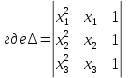 ;
;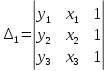 ;
;