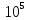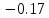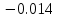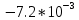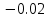Анализ сигналов и систем. Kursovaya_Rabota_АСИС. Пояснительная записка к курсовой работе Анализ сигналов и систем
 Скачать 1.47 Mb. Скачать 1.47 Mb.
|
Бигармоническое воздействиеТаблица 13 – Параметры сигналов
На НЭ воздействуют два гармонических сигнала: 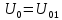 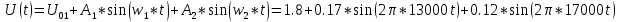   t, c U, B 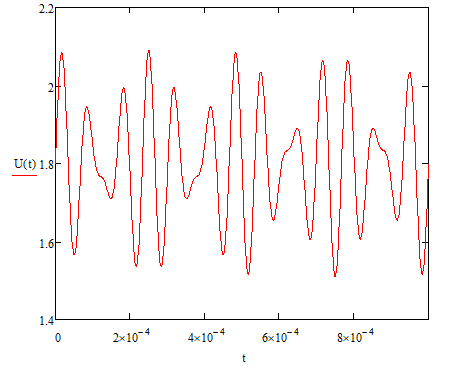 Рисунок 72 – Бигармонический сигнал на входе нелинейного элемента Этот бигармонический сигнал поступает на нелинейный элемент, получим сигнал на выходе нелинейного элемента: 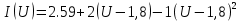 Подставив в формулу выражение для бигармонического сигнала, получим сигнал на выходе нелинейного элемента: 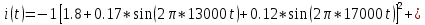 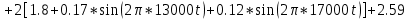   t, c I, A 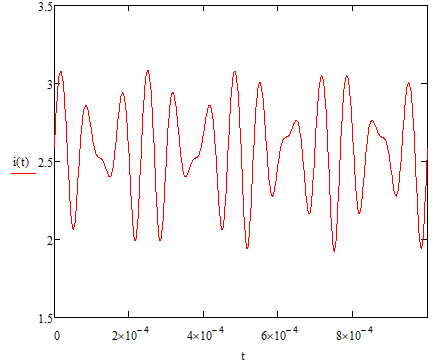 Рисунок 73 – Бигармонический сигнал на выходе нелинейного элемента Для упрощения расчётов рассмотрим слабо нелинейный режим, то есть, когда достаточно учитывать только линейный и квадратичный члены полинома. 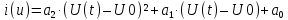 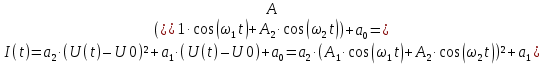 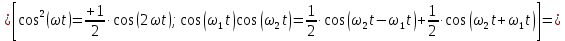 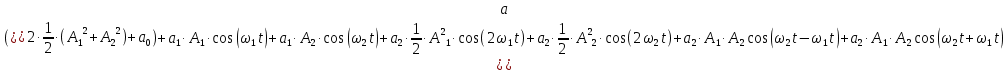 На выходе появляются дополнительные составляющие на комбинационных частотах, которые можно посчитать по формулам: 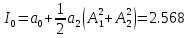 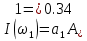 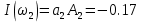 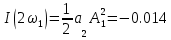 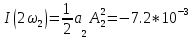 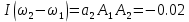 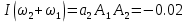 Таблица 14 – Составляющие спектра бигармонического сигнала
 I, A  w, Гц 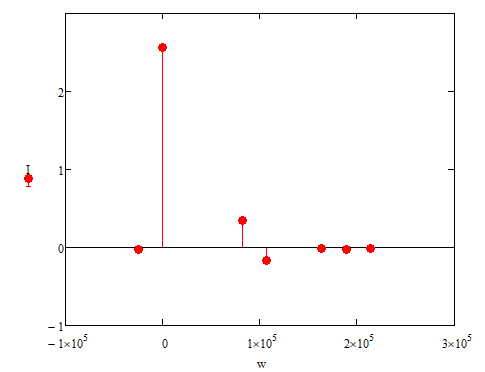 Рисунок 74 – Спектр бигармонического сигнала на выходе нелинейного элемента Моделирование нелинейного элемента в пакете OrCad 16.5Рассмотрим прохождение заданного гармонического сигнала с параметрами: A=0.17В, f=13кГц, через нелинейный элемент GPOLY, настроенный в соответствии с ВАХ, заданной в задании. Коэффициенты: 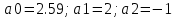 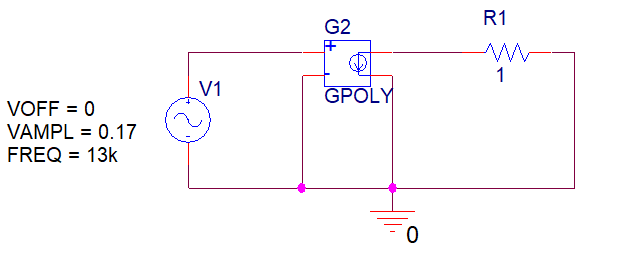 Рисунок 75 - Схема, моделирующая воздействие на НЭ гармонического сигнала  Рисунок 76 – Напряжение на входе V(V1:+) и ток на выходе I(R1) НЭ при воздействии гармоническим сигналом  Рисунок 77 – Спектры напряжения на входе V(V1:+) и тока на выходе I(R1) НЭ при воздействии гармоническим сигналом Теперь рассмотрим случай прохождения через нелинейный элемент бигармонического сигнала с параметрами: A1=0.17В, f1=13кГц и A2=0.12В, f2=17кГц 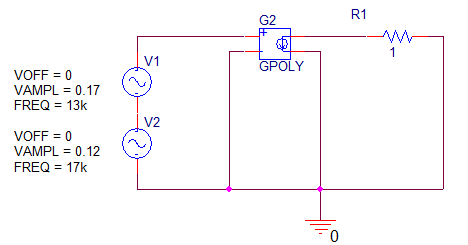 Рисунок 78 – Схема, моделирующая воздействие на НЭ бигармонического сигнала 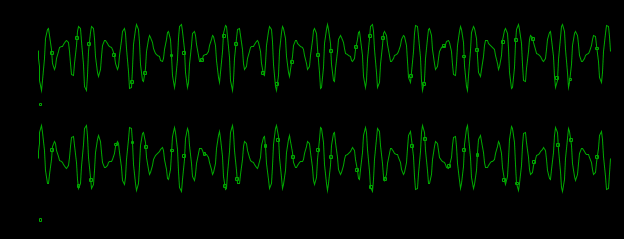 Рисунок 79 - Напряжение на входе V(V1:+) и ток на выходе I(R1) НЭ при воздействии бигармоническим сигналом 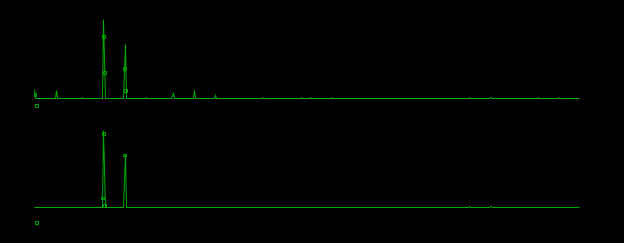 Рисунок 80 – Спектры напряжения на входе V(V1:+) и тока на выходе I(R1) НЭ при воздействии бигармоническим сигналом Теперь рассмотрим случай прохождения через нелинейный элемент исследуемого сигнала. 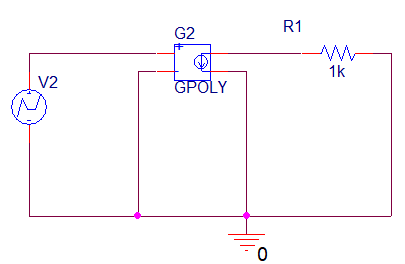 Рисунок 81 – Схема, моделирующая воздействие на НЭ исследуемого сигнала 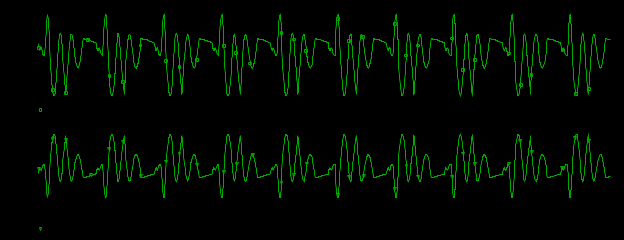 Рисунок 82 – Сигнал на входе V(V2;+) и выходе I(R1) НЭ при воздействии исследуемым сигналом 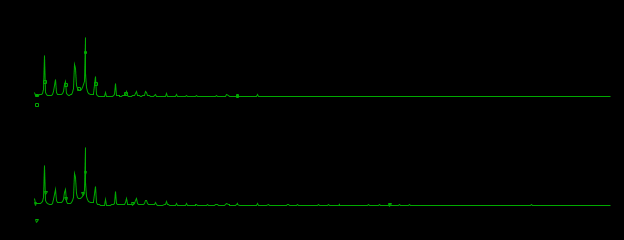 Рисунок 83 – Спектры сигнала на входе V(V2;+) и выходе I(R1) НЭ при воздействии исследуемым сигналом РАСЧЕТ СИГНАЛА НА ВЫХОДЕ ЦЕПИ С ИСПОЛЬЗОВАНИЕМ ИНТЕГРАЛА ДЮАМЕЛЯЗаданная цепь приведена на рисунке 84. 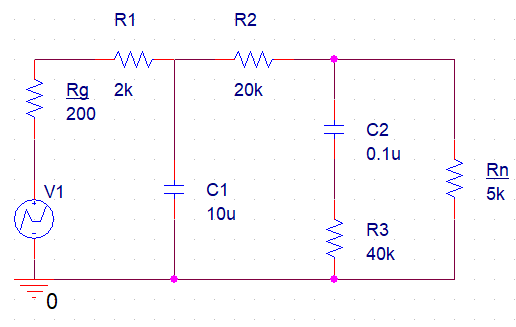 Рисунок 84 – Заданная цепь Приведём результаты, полученные в пакете программ OrCAD. 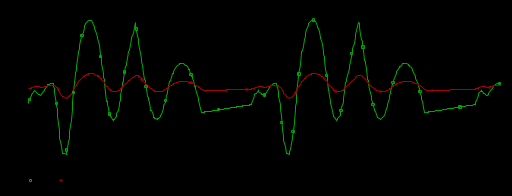 Рисунок 85 – Входной V(V1:+) и выходной V(Rn:2) сигналы Формула интеграла Дюамеля имеет вид: 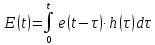 где h(t) – импульсная характеристика цепи. Для нахождения импульсной характеристики цепи наиболее целесообразно найти напряжение на выходном элементе цепи, изображённой на рисунке 86, установив источник 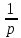 : :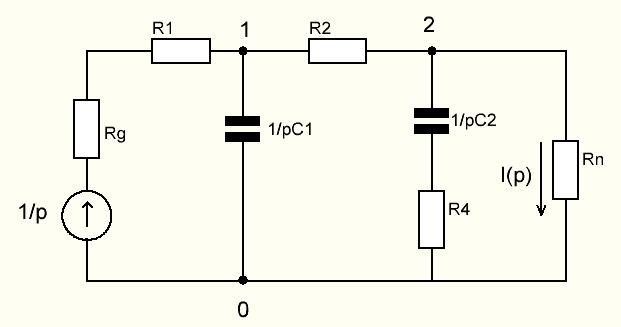 Рисунок 86 – заданная цепь Найдём напряжение с помощью метода узловых потенциалов, используя пакет Mathcad 15: 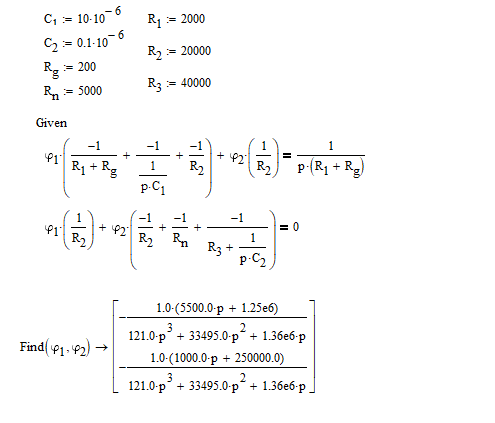 Потенциал во втором узле является выходным напряжением Uout(p). 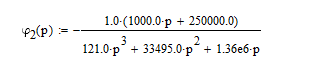 Нйдём обратное преобразование Лаппласа от функции Uout(p). Найденная функция является передаточной функцией цепи 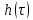 : :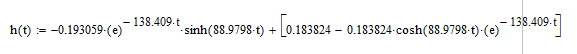 Чтобы найти реакцию цепи Uout(t) на наш сигнал Uin(t) запишем интегралы Дюамеля следующим образом : Чтобы найти реакцию цепи Uout(t) на наш сигнал Uin(t) запишем интегралы Дюамеля следующим образом :для интервала времени от 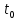 до до 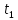 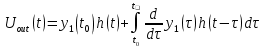 для интервала времени от 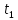 до до 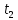 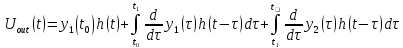 для интервала времени от 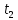 до до 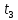 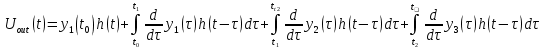 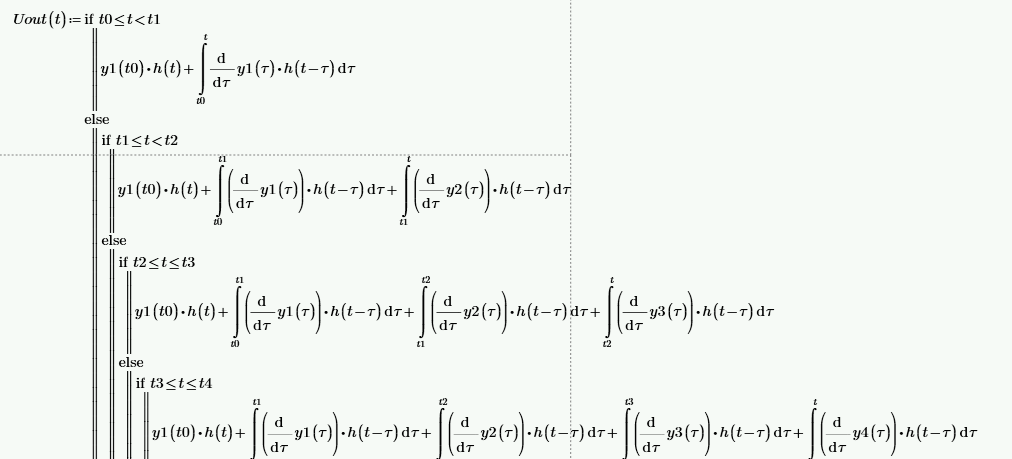 И так далее вплоть до интервала времени 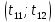 . График получившегося сигнала на выходе изобразим на рисунке 87 . График получившегося сигнала на выходе изобразим на рисунке 87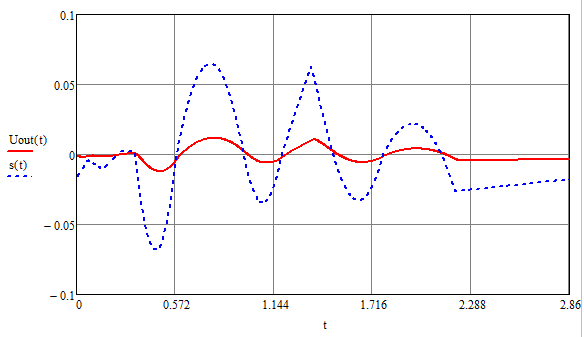 Рисунок 87 - выходной сигнал Uout(t), входной сигнал U(t) ЗАКЛЮЧЕНИЕВ ходе выполнения данной курсовой работы были закреплены изученные ранее методы анализа сигналов. В данной работе был проведён многогранный анализ энцефолограммы. С помощью преобразования Фурье был изучен спектр периодического и непериодического исходных сигналов. Далее были рассмотрены некоторые свойства преобразования Фурье: сдвиг по временной оси, изменение масштаба времени, дифференцирование и интегрирование сигнала, сложение сигналов, разложение сигнала. Проведено восстановление исходного сигнала по спектру. В курсовой работе были рассчитаны энергетические параметры сигнала: средняя мощность и энергия периодического сигнала и энергия непериодического сигнала. Было реализовано ограничение сигнала по уровню 90% его полной энергии. Было рассмотрено влияние действия НЧ и ВЧ помехи на сигнал и их последующее подавление с использованием активного фильтра. В данной работе был разработан активный заграждающий фильтр второго порядка с двойным Т-образным мостом. Использование данного типа фильтра позволяет эффективно подавить помехи. Изучено прохождение сигнала через нелинейный элемент. Проведена степенная, кусочно-линейная аппроксимация ВАХ нелинейного элемента. Рассмотрено прохождение гармонического и бигармонического сигнала через нелинейный элемент. Проведено моделирование воздействия нелинейного элемента на входной сигнал в пакете OrCAD16.5. Получен сигнал на выходе цепи с помощью интеграла Дюамеля. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВГоноровский, И.С. Радиотехнические цепи и сигналы [Текст]: Учебное пособие для вузов / И.С. Гоноровский, Демин М.П. – 5-е издание, переработанное и дополненное. – М.: Радио и связь, 1994. – 481 с. Баскаков, С.И. Радиотехнические цепи и сигналы [Текст]: Учебник для вузов по специальности Радиотехника / С.И. Баскаков. – 2-е издание, переработанное и дополненное – М.: В.Ш., 1988 – 448 с. Разевиг, В.Д. Применение программ P-CAD и PSpice для схемотехнического моделирования на ПВЭМ: В 4 выпусках. Выпуск 3: Моделирование аналоговых устройств [Текст] / В.Д. Разевиг. – М. : Радио и связь, 1992. – 21 с. – 32 с., 120 с. Титце, У. Полупроводниковая схемотехника [Текст]: Справочное руководство / У. Титце, К. Шенк; Перевод с немецкого под редакцией доктора технических наук Алексенко А.Г. – М.: Мир, 1982. – 512 с. Джонсон, Д. Справочник по активным фильтрам[Текст] / Д. Джонсон, Г. Мур. – М.: Энергоатомиздат, 1983. – 128 с. |

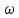 , рад/с
, рад/с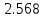
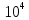
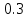 4
4