Анализ сигналов и систем. Kursovaya_Rabota_АСИС. Пояснительная записка к курсовой работе Анализ сигналов и систем

• Название: Пояснительная записка к курсовой работе Анализ сигналов и систем
• Анкор: Анализ сигналов и систем
• Дата: 12.04.2023
• Размер: 1.47 Mb.
• Имя файла: Kursovaya_Rabota_АСИС.docx
• Тип: Пояснительная записка; #1058243
• страница: 10 из 12

4 ИССЛЕДОВАНИЕ ПРОХОЖДЕНИЯ СИГНАЛА ЧЕРЕЗ НЕЛИНЕЙНЫЙ ЭЛЕМЕНТ

4. Аппроксимация степенным полиномом

Для проведения анализа и расчета нелинейных цепей необходимо знать ВАХ или иные аналогичные характеристики нелинейных элементов в аналитической форме. Реальные характеристики имеют довольно сложный вид, затрудняющий точное их описание с помощью простого аналитического выражения. В технике широкое распространение получили способы представления характеристик относительно простыми функциями, лишь приближенно отображающими истинные характеристики. Замена истинной характеристики приближенно представляющей ее функцией называется аппроксимацией характеристики.

Выбор оптимальной аппроксимации зависит от вида нелинейной характеристики, а также от режима работы нелинейного элемента. Одним из наиболее распространенных способов аппроксимации яв­ляется аппроксимация степенным полиномом.

Запишем аппроксимирующий степенной полином в форме: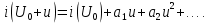



Если под нелинейным элементом подразумевается транзистор, то i — ток коллектора, а u — напряжение, например, между базой и эмиттером.

Коэффициенты a₁, а₂, а₃, ... определяются выражениями: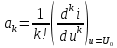



В нашем случае ВАХ нелинейного элемента задана в табличной форме.

Таблица 8 – Координаты ВАХ нелинейного элемента

U, В	0	0,5	1	1,5	2	2,5
I, А	0	0,4	1	1,9	2,95	3,5

Заданная ВАХ нелинейного элемента имеет вид, представленный на рисунке 63: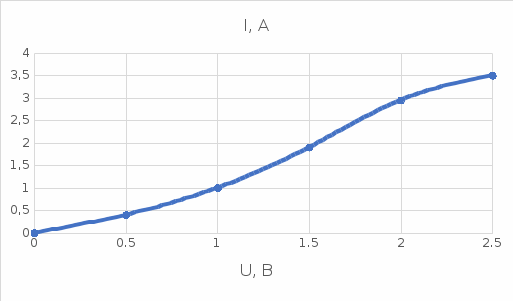



Рисунок 63– ВАХ нелинейного элемента

Точка аппроксимации 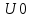выбирается, согласно заданию в таблице 3 ( .

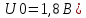Аппроксимируем заданную ВАХ полиномом второй степени. Находим уравнение аппроксимирующей функции по 3-м точкам с координатами (1,5; 1,9), (2; 2,95), (2,5; 3,5).

Берём эти три точки, так как они лежат вблизи рабочей точки.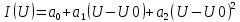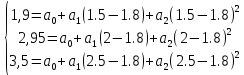





Решаем систему уравнений в системе Mathcad 15 и получаем следующее уравнение: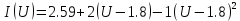



Построим аппроксимированную ВАХ, рассчитав значения аппроксимирующей функции в заданном диапазоне:

U, B

I A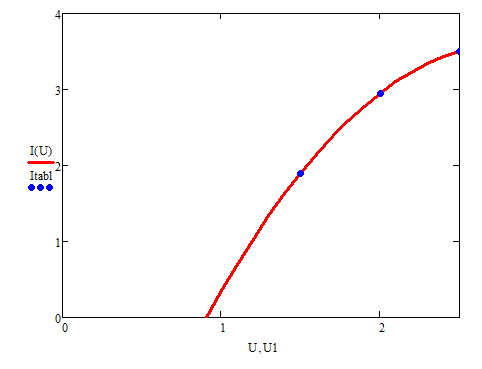


Рисунок 64 - Степенная аппроксимированная ВАХ нелинейного элемента

Пусть на вход нелинейного элемента поступает гармоническое колебание с параметрами:

Таблица 9 – Параметры гармонического сигнала

№	13
U0,В	1,8
A,В	0,17
f,кГц	13

U, В


t, c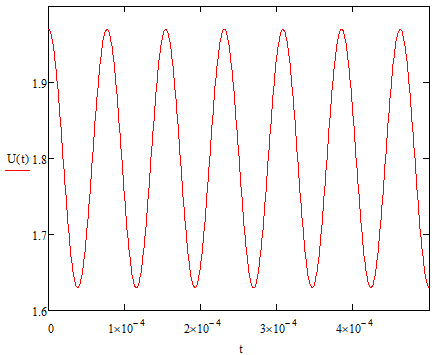


Рисунок 65 – Сигнал на входе нелинейного элемента

Входное напряжение преобразуется в выходной ток: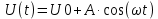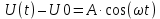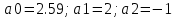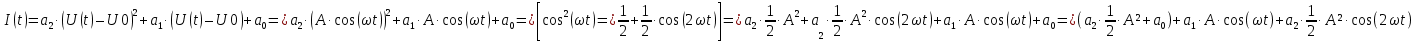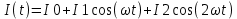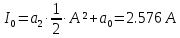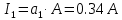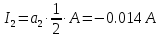


















I, А



t, c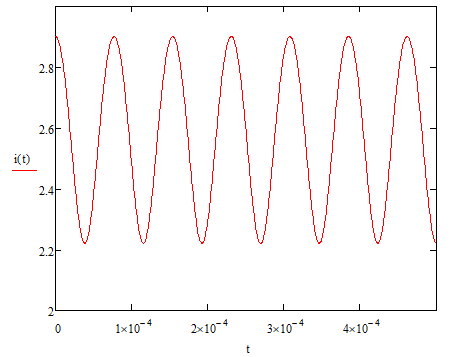


Рисунок 66 – Сигнал на выходе нелинейного элемента


f, Гц

I, A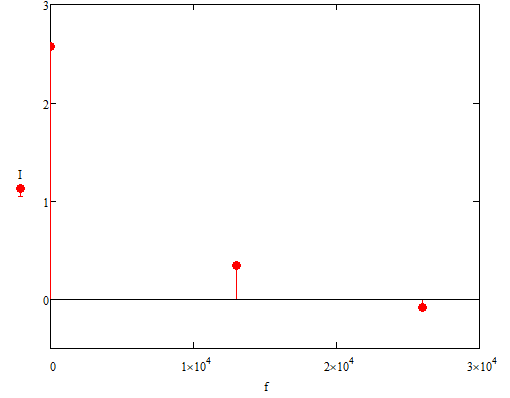



Рисунок 67 – Спектр сигнала на выходе нелинейного элемента

Из рисунка и приведенного выше выражения видны следующие особенности ВАХ при гармоническом воздействии:

- ток покоя i(U0) получает приращение, обусловленное коэффициентами a2,a4… при четных степенях полинома;

- амплитуда I1 гармоники основной частоты ω1 связана с амплитудой возбуждения Um нелинейным соотношением, обусловленным нечетными степенями полинома;

- ток i(t) содержит высшие гармоники с частотами nω1, кратными частоте воздействия ω1.