Анализ сигналов и систем. Kursovaya_Rabota_АСИС. Пояснительная записка к курсовой работе Анализ сигналов и систем
 Скачать 1.47 Mb. Скачать 1.47 Mb.
|
Дифференцирование и интегрирование сигналаДифференцирование сигнала s1(t) можно трактовать как почленное дифференцирование всех гармонических составляющих, входящих в его спектр. Но производная функции еiωt равна iωeiωt, из чего непосредственно вытекает следующие соответствия: 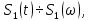 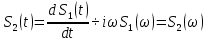 К этому же результату можно прийти так же из общего преобразования Фурье: 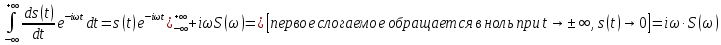 Аналогично: 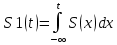 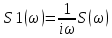   w, Гц U, B 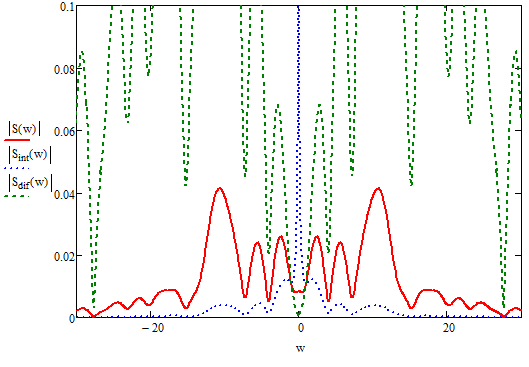  Θ, рад Рисунок 18 – АЧХ исходного S(w), интегрированного Sint(w) и дифференцированного Sdif(w)сигналов  w, Гц 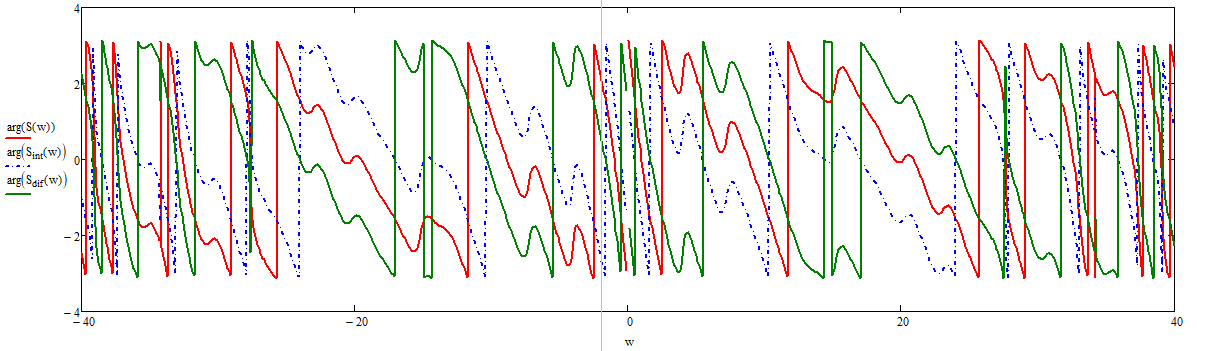 Рисунок 19 – ФЧХ исходного S(w), интегрированного Sint(w) и дифференцированного Sdif(w)сигналов Вывод: спектр продифференцированного сигнала отличается от спектра исходного сигнала множителем iω. При дифференцировании скорость изменения сигнала во времени возрастает. Модуль спектра производной имеет большие значения в области высоких частот по сравнению с модулем спектра исходного сигнала. При интегрировании происходит ослабление высокочастотных спектральных составляющих. Сложение с прямоугольным импульсомПараметры прямоугольного импульса: А*= 40 мВ, t= 0,15 с, Т= 0,85 с.   t, c U, B 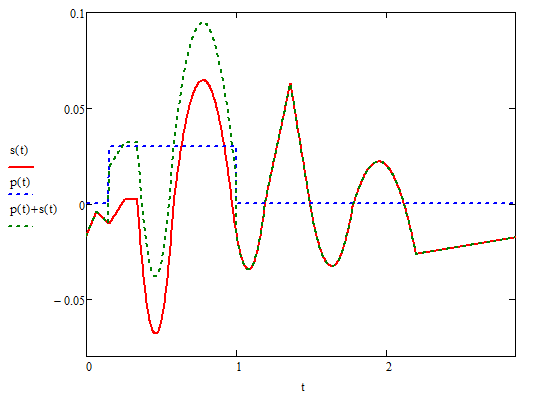  U, B Рисунок 20 – Сложение сигнала с прямоугольным импульсом  w, Гц 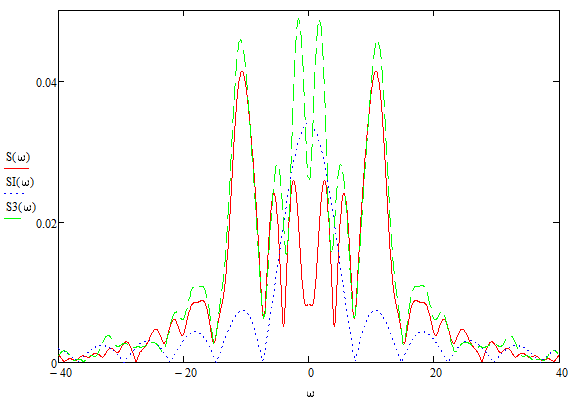  Θ, рад Рисунок 21 – АЧХ исходного сигнала S(w), прямоугольного импульса SI(w) и суммарного сигнала S3(w)  w, Гц 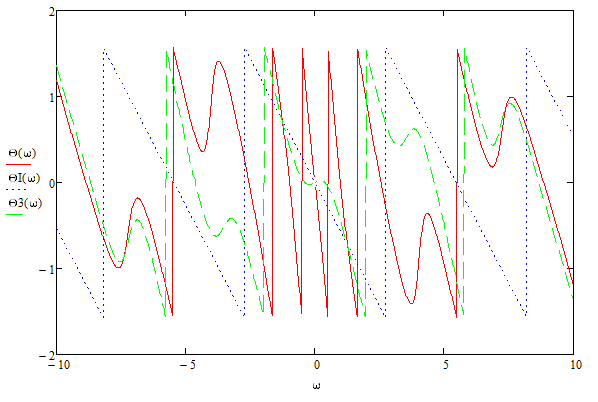 Рисунок 22 – ФЧХ исходного сигнала Θ(w), прямоугольного импульса ΘI(w) и суммарного сигнала Θ3(w) Вывод: так как преобразование Фурье, определяющее спектральную плотность заданной функции времени, является линейным, очевидно, что при сложении сигналов s1(t), s2(t),…, обладающих спектрами S1(ω), S2(ω),…, суммарному сигналу s(t)=s1(t) + s2(t) + … соответствует спектр S(ω)=S1(ω) + S2(ω) + …. Расщепление сигналаПусть 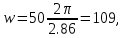 в результате получим: в результате получим:  w, Гц U, B 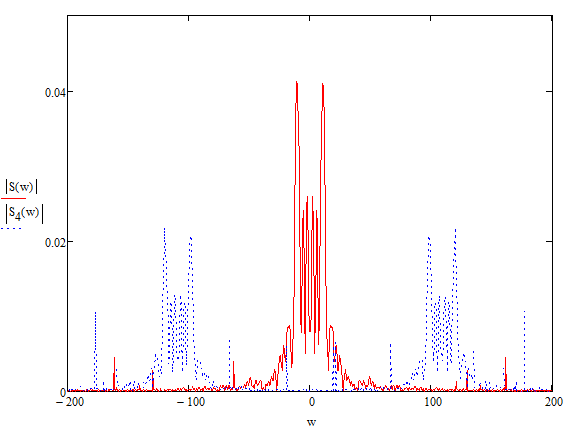 Рисунок 23 – АЧХ исходного S(w) и расщепленного S4(w) сигналов   Θ, рад w, Гц 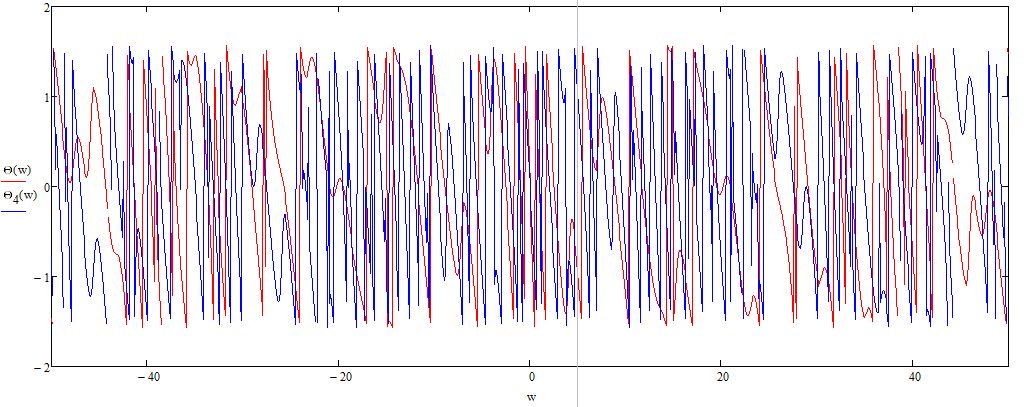 Рисунок 24 – ФЧХ исходного Θ(w) и расщепленного Θ4(w) сигналов Вывод: спектр смещается влево и вправо на ± 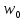 . . |
