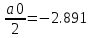Анализ сигналов и систем. Kursovaya_Rabota_АСИС. Пояснительная записка к курсовой работе Анализ сигналов и систем
 Скачать 1.47 Mb. Скачать 1.47 Mb.
|
ИССЛЕДОВАНИЕ СПЕКТРАЛЬНЫХ ХАРАКТЕРИСТИК СИГНАЛАПостроение АЧХ и ФЧХ спектра периодического сигналаДля анализа сигналов и их обработки важное значение имеет разложение заданной функции f(x) по различным ортогональным системам. Бесконечная система действительных функций φ0(x), φ1(x), …φn(x) называется ортогональной на отрезке 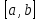 , если , если 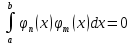 , ,При n≠m При этом предполагается, что 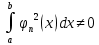 т.е. ни одна из функций рассматриваемой системы не равна тождественно нулю. В математике доказывается, что если функции φn(x) непрерывны, то произвольная кусочно-непрерывная функция f(x), для которой выполняется условие 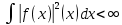 может быть представлена в виде суммы ряда f(x) = C0φ0(x)+ C1φ1(x)+…+Cnφn(x)+…. Для точного разложения сигнала на простейшие ортогональные функции чаще всего используется система основных тригонометрических функций - синусов и косинусов. Это объясняется рядом причин. Во-первых, гармоническое колебание является единственной функцией времени, которая сохраняет свою форму при прохождении через любую линейную цепь (с постоянными параметрами). Изменяются лишь амплитуда и фаза колебания. Во-вторых, разложение сложного сигнала по синусам и косинусам позволяет использовать символический метод, разработанный для анализа передачи гармонических сигналов через линейные цепи. Так как функция, аппроксимирующая заданный сигнал, периодическая, то ее можно представить в виде суммы ряда Фурье в тригонометрической форме, коэффициенты которого вычисляются по формулам: 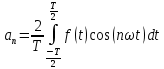 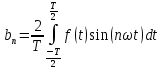 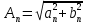 где Т – интервал ортогональности, совпадающий с периодом функции f(t), а 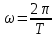 - частота основной гармоники. - частота основной гармоники.Совокупность коэффициентов An называется частотным спектром периодического сигнала. Фаза n - ой гармоники определяется по формуле: 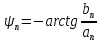 Теоретически несинусоидальный сигнал имеет бесконечный спектр, для анализа рекомендуется ограничиться набором гармоник с частотами, меньшими 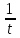 . .Пусть n = 0…25; Т=2,860 с; ω = 2,197 рад/с = 0,349 Гц. Первую гармонику вычислим вручную. Так как наша сложная функция представляет собой последовательность из прямых и парабол, решим отдельно в общем виде интегралы от прямой kt+b, и от параболы at2+dt+c. А уже после подставим коэффициенты k, b, a, d, c и интервалы времени (tn;tn+1) в общее решение, для нахождения a1 и b1. Интегралы от парабол: 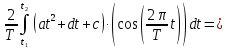 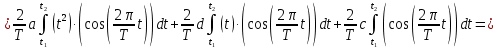 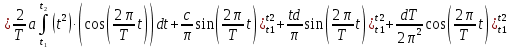 Первый интеграл решим отдельно: 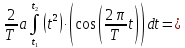 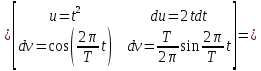 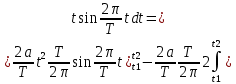 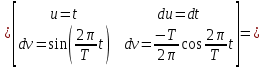 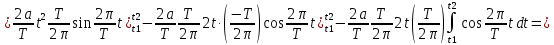 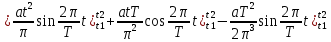 Тогда: 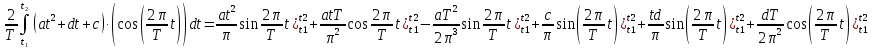 Получившееся решение для интеграла от функции вида at2+dt+c коэффициента a1 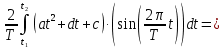 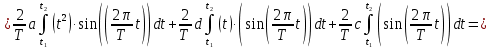 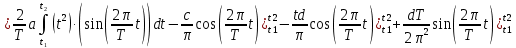 Первый интеграл решим отдельно: 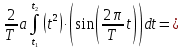 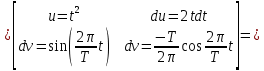 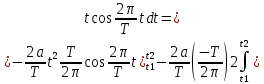 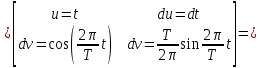 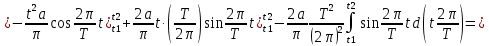 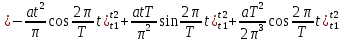 Тогда: 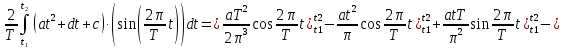 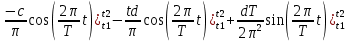 Получившееся решение для интеграла функции вида at2+dt+c коэффициента b1 Интегралы от функции вида kt+b: 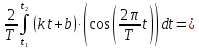 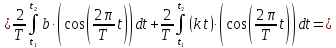 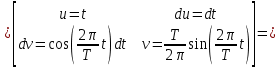 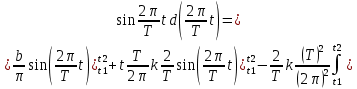 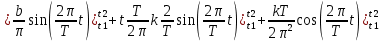 Получившееся решение для интеграла от функции вида kt+b коэффициента a1 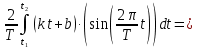 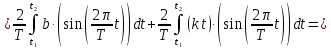 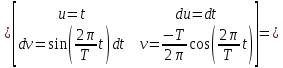 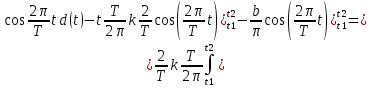 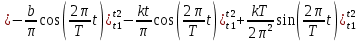 Получившееся решение для интеграла от функции вида kt+b коэффициента b1. Подставим в полученные решения коэффициенты k, b, a, d, c, интервалы времени (tn;tn+1) и просуммируем их соответственно. Таким образом получим коэффициенты a1 b1 первой гармоники.     И так, И так,a1 = 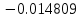 b1 = 0.00963 Найдем амплитуду и фазу первой гармоники по соответствующим формулам: 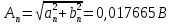 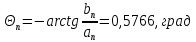 Рассчитаем коэффициенты ряда Фурье, а также амплитуду и фазу первых 25 гармоник сигнала при помощи математического пакета Mathcad. Коэффициент 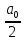 находится по формуле: находится по формуле: Результаты расчета представлены в таблице 6. АЧХ и ФЧХ непериодического сигнала представлены на рисунках 6 и 7 соответственно. Таблица 6 – Значения коэффициентов ряда Фурье, АЧХ и ФЧХ сигнала
  n,  U,В 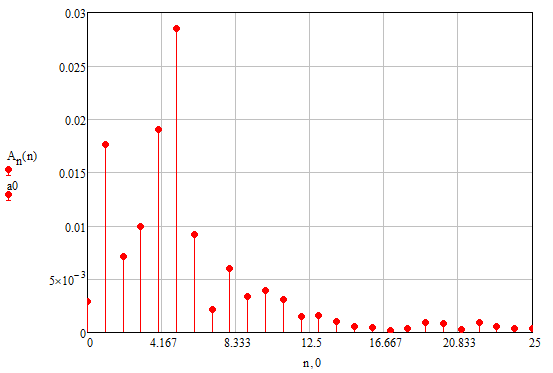 Рисунок 6 – АЧХ периодического сигнала   Θ, рад n,  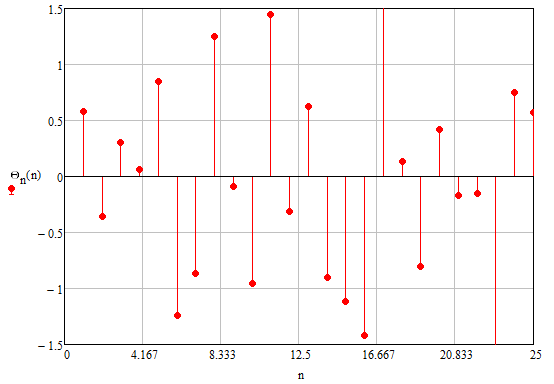 Рисунок 7 – ФЧХ периодического сигнала |