Анализ сигналов и систем. Kursovaya_Rabota_АСИС. Пояснительная записка к курсовой работе Анализ сигналов и систем
 Скачать 1.47 Mb.
|
Энергия в спектре непериодического сигналаДля получения выражения для непериодического сигнала воспользуемся выражением, которое при выполнении условия f(t)=g(t)=s(t), определяет полную энергию сигнала 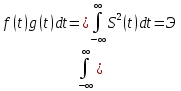 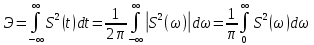 Это важное соотношение, устанавливающее связь между энергией сигнала (выделяемой на сопротивлении 1ом) и модулем его спектральной плотности, известно под названием равенство Парсеваля. Величина 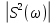 имеет смысл энергии, приходящейся на 1 Гц, и рассматривается как спектральная плотность энергии.Энергия данного сигнала: 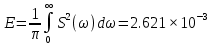 Энергия непериодического сигнала не зависит от фазировки спектральных составляющих. Это является, как и для периодического сигнала, результатом ортогональности спектральных составляющих. Различие заключается лишь в интервалах ортогональности: период Т для периодического сигнала и бесконечно большой интервал для непериодического сигнала. Между сигналом s(t) и его спектром S(ω) существует однозначное соответствие. Для практических приложений важно установить связь между преобразованием сигнала и соответствующим этому преобразованию изменением спектра. Из многочисленных возможных преобразований сигнала рассмотрим следующие, наиболее важные: сдвиг сигнала во времени, изменение масштаба времени, сложение сигналов, дифференцирование, интегрирование сигнала. Сдвиг сигнала во времениПусть сигнал s1(t) произвольной формы существует на интервале времени от t1 до t2 и обладает спектральной плотностью S1(ω). При задержке этого сигнала на время t0 получим новою функцию времени s(t2)=s(t – t0), существующую на интервале от t1+t0 до t2+t0. Спектральная плотность сигнала s1(t) равна 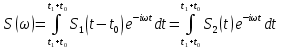 Получаем: 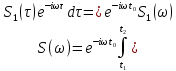 Из этого соотношения видно, что сдвиг во времени функции s(t) на ±t0 приводит к изменению фазовой характеристики спектра S(ω) на величину ±ωt0. Амплитудно-частотная характеристика спектра от положения сигнала на оси не зависит. Сдвиг сигнала во времени осуществляется на величину t = 0,572 с  t, c U, B 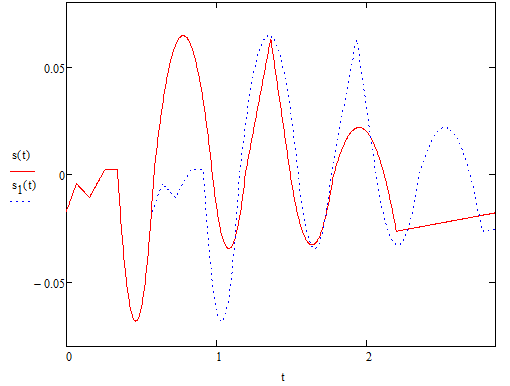 Рисунок 12 – Исходный U(t) и задержанный s1(t) сигналы w, Гц U, B 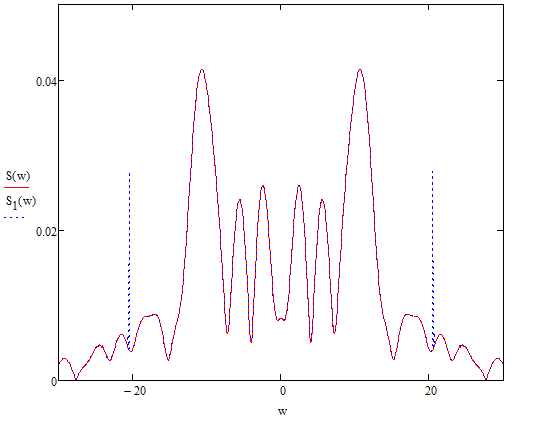 Рисунок 13 – АЧХ исходного S(w) и сдвинутого S1(w) сигналов w, Гц Θ, рад 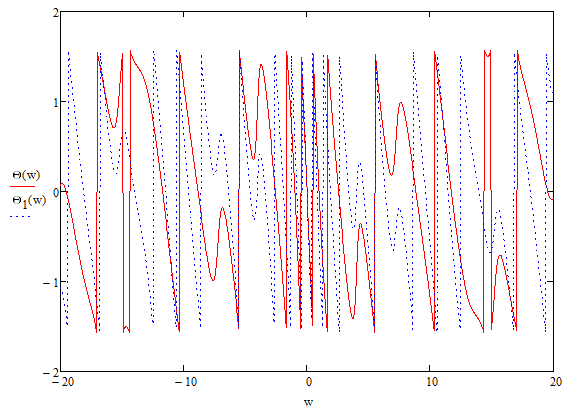 Рисунок 14 – ФЧХ исходного Θ(w) и сдвинутого Θ1(w) сигналов Вывод: cдвиг во времени функции s(t) на ±t0 приводит к изменению фазовой характеристики спектра S(ω) на величину ±ωt0. Амплитудно-частотная характеристика спектра от положения сигнала на оси времени не зависит. Пусть сигнал s1(t) подвергается сжатию во времени. Новый сжатый сигнал s2(t) связан с исходным соотношением s2(t)=s1(nt), n>1. Спектральная плотность сжатого импульса: 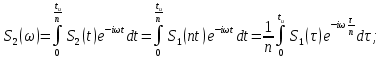 Получаем: 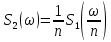 Пусть n=2. t, c U, B 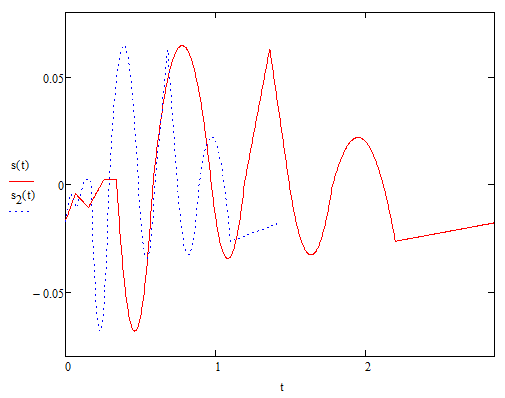 Рисунок 15 – Исходный s(t) и сжатый s2(t) сигналы w, Гц U, B 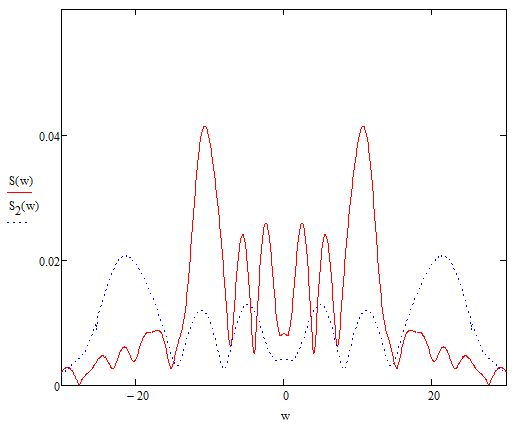 Рисунок 16 – АЧХ исходного S(w) и сжатого S2(w) сигналов   w, Гц Θ, рад 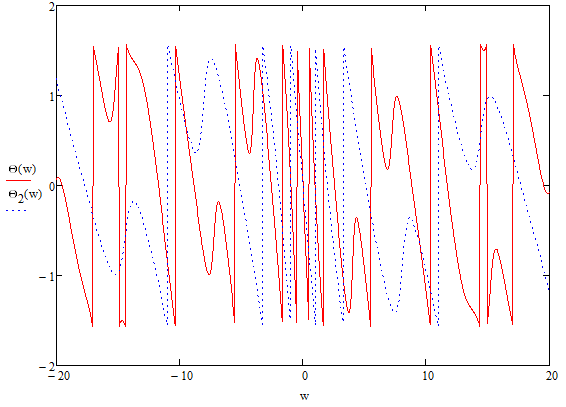 Рисунок 17 – ФЧХ исходного Θ(w) и сжатого Θ2(w) сигналов Вывод: при сжатии сигнала в n раз на временной оси во столько же раз расширяется его спектр на оси частот. Модуль спектральной плотности при этом уменьшится в n раз. Очевидно, что при растягивании сигнала во времени (т.е. при n<1) имеет место сужение спектра и увеличение модуля спектральной плотности. |