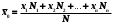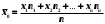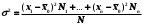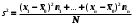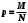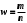Пояснительная записка курса по выбору Задачи по теории вероятностей и математической статистики, для обучающихся основной школы

• Название: Пояснительная записка курса по выбору Задачи по теории вероятностей и математической статистики, для обучающихся основной школы
• Дата: 18.10.2022
• Размер: 148.74 Kb.
• Имя файла: 1 (1).docx
• Тип: Анализ; #740735
• страница: 5 из 6

Занятие 12

1. 
   Найти дисперсию дискретной случайной величины Х и построить многоугольник распределения, заданной законом распределения:
   

Х	-8	42	51
р	0,12	0,48	0,4
Х	0,35			0,5	0,1
р	0,43			0,27	0,3

1. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 р. и десять выигрышей по 1 р. Найти закон распределения случайной величины Х – стоимости возможного выигрыша для владельца лотерейного билета.

2. 
   Дискретная случайная величина имеет только 2 возможных значения х и у, причем x

Занятие 13

Рассмотрим базовые понятия математической статистики.

По определению, генеральной совокупностью является некоторое количество объектов, которые поддаются исследованию.

Определенное количество объектов генеральной совокупности, которое отбирается для изучения, является выборкой.

Количество изучаемых объектов генеральной совокупности является объемом. Как правило, объем генеральной совокупности может быть как конечным так и бесконечным.

Существует несколько видов выборок:

• 
  собственно – случайная выборка (при определении элементов не задаются определенные правила, отсутствует разделение данных);
  
• 
  механическая выборка (между её элементами выбирается определенный промежуток);
  
• 
  типическая выборка (выбор случайным образом элементов из типических групп, на которые по некоторому признаку разбивается генеральная совокупность)
  
• 
  серийная выборка (случайным образом отбираются целые группы совокупности, а сами серии подвергаются сплошному наблюдению)
  

Выделяют следующие способы образования выборки:

• 
  повторный выбор – один элемент выборки может несколько раз использоваться несколько раз при исследовании.
  
• 
  бесповторный отбор – когда обратный элемент не возвращается в общую совокупность.
  

Наименование характеристики	Генеральная совокупность	Выборка
Математическое ожидание
Дисперсия
Доля

Где х_i – значение признака.

N и n – объемы генеральной и выборочной совокупностей.

N_i и n_i – число элементов генеральной и выборочной совокупностей со значением признака х_i

M и m – число элементов генеральной и выборочной совокупностей, обладающих данным признаком