Пояснительная записка курса по выбору Задачи по теории вероятностей и математической статистики, для обучающихся основной школы
 Скачать 148.74 Kb. Скачать 148.74 Kb.
|
Занятие 8Рассмотрим определение полной группы событий. Допустим, имеется некоторая совокупность событий А1, А2, …, Аn. Данная совокупность будет образовывать полную группу событий при выполнении следующих условий: а) она описывает все возможные исходы; б) события попарно независимы и не совместны. Допустим, имеется некоторое событие А, которое может наступить только при появлении одного из несовместных событий В1, В2,…, Вn. Данные события как раз образуют полную группу. Параллельно, известны условные вероятности 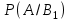 , , 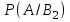 , …, , …, 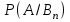 . Вопрос состоит в том, как найти вероятность события А? . Вопрос состоит в том, как найти вероятность события А? Вероятность события А будет определятся следующим образом: 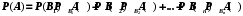 . .Данная формула носит название формулы полной вероятности. Рассмотрим следующую задачу: Допустим существует некоторое событие А, наступление которого зависит от выполнения одного из несовместных событий В1, В2,…, Вn, которые образуют полную группу. По условию, нет никакой информации о том, какое именно из событий В1, В2,…, Вn наступит, следовательно, каждое из этих событий является гипотезой. Предположим, что в результате проведения опыта появилось событие А. Нужно узнать, как изменились вероятности гипотез при наступлении события А, то есть нужно найти условные вероятности вида: 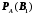 , , 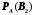 , …, , …, 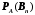 . .Определить данные вероятности можно при помощи формулы Бейеса: 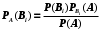 , ,Заменив 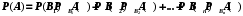 получим: получим: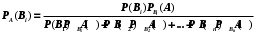 . .Решим следующую задачу: на трех заводах в совокупности изготовлено 1000 лампочек. На первом заводе изготовлено 200 лампочек, на втором 460, а на третьем 340. Найти вероятность того, что наугад взятая лампочка является неисправной. Вероятность производства неисправной лампочки на каждом из заводов равна соответственно 0,03, 0,02, 0,01. Решение: Полагаем, что A – событие, состоящее в том, что взятая наугад лампочка неисправная. Н1, Н2, Н3, гипотезы, что они изготовлены соответственно 1-м, 2-м или 3-м заводе. Вероятности для гипотез равны: P(H1)=200/1000=0.2, P(H2)=460/1000=0.46, P(H1)=340/1000=0.34. Из условия задачи следует, что р1=РН1(А)=0,03; р2=РН2(А)=0,02; р3=РН3(А)=0,01. Найдем вероятность того, что неисправная лампочка, изготовлена 1-м заводом. По формуле Бейеса имеем: 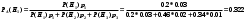 Занятие 9Две юридические компании предоставляют услуги по защите граждан в суде. Вероятность того, что первая компания победит в судебном процессе равна 0,74, а вероятность того, что вторая компания победит в судебном процессе равна 0,55. Найти вероятность того, что одна из компаний проиграет в судебном процессе. Какова вероятность того, что проигравшей компанией окажется первая? Во время испытаний было установлено, что вероятность безотказной работы прибора при отсутствии повреждений равна 0,99, при перегреве – 0,95, при вибрации – 0,9, при вибрации и перегреве – 0,8. Найти вероятность P1 отказа этого прибора во время работы в жарких странах (вероятность перегрева – 0,2, вибрации – 0,1) и вероятность P2 отказа во время работы в передвигающейся лаборатории (вероятность перегрева – 0,1, вибрации – 0,3), если считать перегрев и вибрацию независимыми событиями. Домашнее задание Первая компании производит в два раза больше продукции второй. Вероятность того, что продукция окажется бракованной равна 0,3 на первой компании, на второй 0,2. Наугад взятая продукция оказалась качественной. Какова вероятность того, что эта деталь выпущена второй компанией? Среди женщин – избирателей 70% поддерживают кандидата А, а среди мужчин 60%. Используя данные переписи, согласно которым доля женщин избирателей составляет 55%, оценить вероятность победы на выборах кандидата А. |
