Пояснительная записка курса по выбору Задачи по теории вероятностей и математической статистики, для обучающихся основной школы

• Название: Пояснительная записка курса по выбору Задачи по теории вероятностей и математической статистики, для обучающихся основной школы
• Дата: 18.10.2022
• Размер: 148.74 Kb.
• Имя файла: 1 (1).docx
• Тип: Анализ; #740735
• страница: 4 из 6

Занятие 10

Рассмотрим основные определения касающиеся случайных величин.

Случайной, называется величина, которая в результате проведения опыта может принимать только одно возможно значение, которое определяется из заданных условий задач.

Обычно случайные величины обозначают прописными буквами, а их значения строчными.

На практике приходится иметь дело с дискретными и непрерывными случайными величинами.

Дискретной случайной величиной называется величина, которая может принимать значений, имеющие определенные вероятности. Дискретные случайные величины бывают как конечные так и бесконечные.

Непрерывная случайная величина, это такая величина, которая принимает значения из определенного промежутка. В отличии от дискретных случайных величин, количество значений непрерывной случайной величины только бесконечное.

При табличном задании первая строка содержит возможные значения, а вторая – их вероятности:

Х	x1	x2	…	xn
p	p1	p2	…	pn

Сумма вероятностей второй строки таблицы равна единице: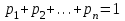

.

Если множество возможных значений Х бесконечно, то ряд 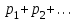сходится и его сумма равна единице.

Занятие 11

Из определения закона распределения для случайной величины следует, что он полностью определяет случайную величину. Зачастую происходит такая ситуация, когда закон не известен, и его нужно ещё получить, путем проведения вычислений. Существуют определенные случайные величины, которые не предполагают построения закона распределения, для их определения достаточно знать числовые характеристики распределения.

Первой такой характеристикой является математическое ожидание случайной величины. Чтобы понять, что такое математическое ожидание можно привести наглядный пример.

Пусть имеется дискретная случайная величина Х, которая может принимать значения х₁, х₂, …, х_n. Вероятности которых соответственно равны р₁, р₂, …, р_n. Тогда математическое ожидание М(Х) случайной величины Х определяется равенством: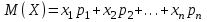

.

Пример: Найти математическое ожидание дискретной случайной величины Х, заданной законом распределения:

Х	-12	28	33
Р	0,33	0,66	0,01

Решение: М(Х)=-12∙0,33+28∙0,66+33∙0,01=14,85

Математическое ожидание приближается к среднему арифметическому всех известных значений случайной величины.

С понятием математического ожидания связанно большое количество прикладных задач. Также существуют задачи, предполагающие нахождения степени рассеяния значений, вокруг среднего значения. Именно такие задачи решает дисперсия.

Определение: Дисперсией случайной величины Х называется математическое ожидание квадрата отклонений случайной величины от ее математического ожидания. Дисперсия обозначается, как D(x)

D(Х)=M[X-М(Х)]²=M[(x-x)²]

Пример: Найти дисперсию случайной величины Х, которая задана следующим законом распределения:

Х	1	2	5
p	0,3	0,5	0,2

Решение. Найдем математическое ожидание: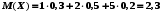

.

По определению: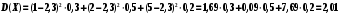

.

Используя формулу D(Х)=M(X)²-[М(Х)]² можно найти дисперсию гораздо быстрее: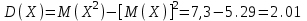

.

Для оценки рассеяния всевозможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и другие величины.

Средним квадратическим отклонением величины Х называют квадратный корень из дисперсии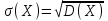