Пояснительная записка курса по выбору Задачи по теории вероятностей и математической статистики, для обучающихся основной школы

• Название: Пояснительная записка курса по выбору Задачи по теории вероятностей и математической статистики, для обучающихся основной школы
• Дата: 18.10.2022
• Размер: 148.74 Kb.
• Имя файла: 1 (1).docx
• Тип: Анализ; #740735
• страница: 2 из 6

Занятие 2

Рассмотрим классические задачи, которые решаются с помощью комбинаторных формул.

1. 
   Для участия в международной олимпиаде по математике отбирается команда из 6 человек. Сколько существует наборов команд, если среди претендентов 31 мальчик и 28 девочек.
   
2. 
   Сколько существует способов выбора 3 дам, 1 короля и 2 десяток из колоды, в которой 52 карты.
   

Занятие 3

1. 
   Сколько существует способов расстановки 17 книг на полке.
   
2. 
   Сколько существует способов рассадки 20 человек за круглым столом таким образом, чтобы 3 определенных человека сидели рядом, а остальные в произвольном порядке.
   

Занятие 4

1. 
   Подбрасываются три игральных кубика. Определить вероятность следующих событий: а) сумма выпавших очков не превышает 21; б) произведение выпавших очков делиться на 4; в) сумма выпавших очков равна 13, а разность равна 1.
   
2. 
   В ящике имеется 10 одинаковых деталей, помеченные номерами 1, 2, …, 10. Наудачу извлечены шесть деталей. Найти вероятность того, что среди извлеченных деталей окажутся: а) деталь №1; б) детали №1 и №2.
   
3. 
   Найти вероятность выиграть в лотерее, если в ней участвуют 100 билетов из которых 14 выигрышных.
   

Занятие 5

Помимо простых событий, бывают и сложные события, которые включают в себя исходы определенного количество более простых событий, по заранее известным вероятностям.

Если событие достоверное, его вероятность равна 1. Если событие невозможное, его вероятность равна 0. Вероятность произведения двух независимых событий вычисляется как произведение вероятностей каждого событий отдельно.

Пример: Абонент пытается набрать номер, но помнить только первые 2 цифры из 5.

Решение. Пусть событие А – “все цифры набраны верно”. Разобьем это событие на более простые. Пусть В – “третья цифра набрана верно“, С – “ четвертая цифра набрана верно“, а D – “пятая цифра набрана верно“. Тогда, А=ВСD по определению произведения событий. Следовательно Р(А)=Р(ВСD). По теореме о вероятности произведения независимых событий Р(ВСD) = Р(В)Р(C)Р(D).

Определение. Условной вероятностью события А, при условии, что произошло событие В, называется отношение вероятностей P(АВ) к Р(В) и обозначается Р_А(В): .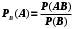

Пример: Производится спасательная операция по поиску двух человек, потерявшихся в лесу. Вероятность найти первого человека независимо от второго равна 0,5. Определить вероятность того, что за определенный промежуток времени, спасателям удастся найти хотя бы одного потерявшегося человека?

Решение. Пусть событие А – “найден хотя бы один из пропавших людей”. Разделим данное событие на простые. Пусть В1 – найдем первый человек, а В2 – найден второй человек.. Следовательно, событие А состоит из суммы событий В1 и В2 по определению суммы событий. Вероятность данного события определяется следующим образом: Р(А)=Р(В1+В2). Учитывая то, что В1и В2 – совместные события, используя теорему о вероятности суммы, получим вероятность исходного события: Р(В1+В2) = Р(В1)+Р(В2)-Р(В1 В2) = 0,5+0,5 – 0,25=0,75.

Занятие 6

1. 
   Человек придумал определенное трехзначное число. Определить вероятность того, что загаданное число будет: а) лежать в пределах от 100 до 300; б) делиться на 14?
   
2. 
   Монета брошена два раза найти вероятность, что хотя бы один раз появится герб.
   

Выполнение домашнего задания является необходимым условием успешного усвоения пройденного материала.

Домашнее задание

1. 
   Урне лежит 4 белых и 5 черных шаров. Наугад вытаскивают 2 шара. Найти вероятность того, что они оба будут белые.
   
2. 
   Найти вероятность того, что из 6 наугад выбранных людей окажутся с карими глазами.
   
3. 
   Студент знает 40 вопросов из 75. Найти вероятность того, что студент сдаст экзамен, если для этого нужно ответить на 2 вопроса.
   

Занятие 7

1. 
   Партия привезенных холодильников проверяется на исправность. Вероятность того, что определенных холодильник исправен равна 0,738. Найти вероятность того, что из 5 наугад взятых телевизоров будет 3 неисправных.
   
2. 
   Брошены три игральные кости. Найти вероятность следующих событий: а) произведение выпавших очков будет делиться на 25; на одной кости выпадет 6, на второй 3, на третьей 1.
   
3. 
   Вероятность сбить утку при одном выстреле из ружья равна 0,88. Какое количество выстрелов нужно сделать охотнику, чтобы с вероятностью, меньшей 0,73 можно было ожидать, что будет сбито 4 утки?
   

Домашнее задание

1. В урне присутствует 5 белых, 4 красных и 3 зеленых шара. Наугад ,из урны достают 6 шаров. Найти вероятность того, среди них будет 3 белых, 2 красных и 1 зеленый шар.

2. 23 студента сдают экзамен. Вероятность сдать экзамен на «5» равна 0,6, на «4» равна 0,7, на «3» равна 0,8, на «2» равна 0,9. Найти вероятности того, что среда 5 студентов: а) 2 сдадут на «5», 3 сдадут на «2»; б) не менее 3 студентов сдадут экзамен на «4».