электив. Пояснительная записка Основной задачей обучения математике в школе является сознательное овладение учащимися системой математических знаний и умений, необходимых в повседневной жизни.
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
|
Пояснительная записка Основной задачей обучения математике в школе является сознательное овладение учащимися системой математических знаний и умений, необходимых в повседневной жизни. Овладение практически любой современной профессией требует тех или иных знаний по математике. Актуальной задачей и миссией школы является определенный портрет выпускника на выходе, имеющем качественные знания по предмету и высокий потенциал в реализации задуманных целей. Задача преподавателя - предметника реализовать не только психолого-педагогическую функцию, но и непосредственно обеспечить ученика всем необходимым набором знаний и умений, которые в дальнейшем он сможет применить и доказать на основном государственном экзамене (ОГЭ). Данная программа элективного курса предназначена для обучающихся 9-х классов общеобразовательных учреждений и рассчитана на 34 часа, 1 час в неделю. Она предназначена для повышения эффективности подготовки обучающихся 9 класса к основному государственному экзамену по математике за курс основной школы и предусматривает их подготовку к дальнейшему обучению в средней школе. Программой школьного курса математики не предусмотрены обобщение и систематизация знаний по различным разделам, полученных учащимися за весь период обучения с 5 по 9 класс. Элективный курс позволит систематизировать и углубить знания учащихся по различным разделам курса математики основной школы (арифметике, алгебре, статистике, теории вероятностей и геометрии). Элективный курс направлен на восполнение недостающих знаний, отработку приемов решения заданий различных типов и уровней сложности вне зависимости от формулировки, а также отработку типовых заданий ОГЭ по математике на тестовом материале. Программа элективного курса составлена на основе Обязательного минимума содержания основных образовательных программ и Требований к уровню подготовки выпускников основной школы. Методы работы в рамках организации элективного курса: Метод группового взаимодействия; Метод делового сотрудничества; Метод самостоятельной работы; Метод кластеров; Метод «Проблемной ситуации» Метод игры; Метод коммуникации (World Сafe); Метод тематической дискуссии; Метод групповой консультации; Метод презентаций; Метод учебного тренажера (на примере конкретной математической среды». Цель элективного курса: систематизация знаний и способов деятельности учащихся по математике за курс основной школы, подготовка обучающихся 9 класса к основному государственному экзамену по математике. Задачи элективного курса: Закрепить основные теоретические понятия и определения по основным изучаемым разделам; Отработать основные типы задач изучаемых типов КИМ ОГЭ Формирование у обучающихся целостного представления о теме, ее значения в разделе математики, межпредметные связи с другими темами; способствовать интеллектуальному развитию учащихся, формированию качеств мышления, характерных для математической деятельности и необходимых ученику для успешной сдачи ОГЭ, для общей социальной ориентации; Акцентировать внимание учащихся на единых требованиях к правилам оформления различных видов заданий, включаемых в итоговую аттестацию за курс основной школы. Способствовать созданию условий осмысленности учения, включения в него обучающегося на уровне не только интеллектуальной, но личностной и социальной активности с применением тех или иных методов обучения. Планируемые образовательные результаты: Предметные результаты: Формирование навыков поиска математического метода, алгоритма и поиска решения задачи в структуре задач ОГЭ; Формирование навыка решения определенных типов задач в структуре задач ОГЭ; уметь работать с таблицами, со схемами, с текстовыми данными; уметь преобразовывать знаки и символы в доказательствах и применяемых методах для решения образовательных задач; приводить в систему, сопоставлять, обобщать и анализировать информационные компоненты математического характера и уметь применять законы и правила для решения конкретных задач; выделять главную и избыточную информацию, производить смысловое сжатие математических фактов, совокупности методов и способов решения; уметь представлять в словесной форме, используя схемы и различные таблицы, графики и диаграммы, карты понятий и кластеры, основные идеи и план решения той или иной математической задачи; Метапредметные результаты обучения Регулятивные УУД определять собственные проблемы и причины их возникновения при работе с математическими объектами; формулировать собственные версии или применять уже известные формы и методы решения математической проблемы, формулировать предположения и строить гипотезы относительно рассматриваемого объекта и предвосхищать результаты своей учебно-познавательной деятельности; определять пути достижения целей и взвешивать возможности разрешения определенных учебно-познавательных задач в соответствии с определенными критериями и задачами; выстраивать собственное образовательное подпространство для разрешения определенного круга задач, определять и находить условия для реализации идей и планов (самообучение); самостоятельно выбирать среди предложенных ресурсов наиболее эффективные и значимые при работе с определенной математической моделью; уметь составлять план разрешения определенного круга задач, используя различные схемы, ресурсы построения диаграмм, ментальных карт, позволяющих произвести логико - структурный анализ задачи; уметь планировать свой образовательный маршрут, корректировать и вносить определенные изменения, качественно влияющие на конечный продукт учебно-познавательной деятельности; умение качественно соотносить свои действия с предвкушаемым итогом учебно-познавательной деятельности посредством контроля и планирования учебного процесса в соответствии с изменяющимися ситуациями и применяемыми средствами и формами организации сотрудничества, а также индивидуальной работы на уроке; умение отбирать соответствующие средства реализации решения математических задач, подбирать инструменты для оценивания своей траектории в работе с математическими понятиями и моделями; Познавательные УУД умение определять основополагающее понятие и производить логико-структурный анализ, определять основные признаки и свойства с помощью соответствующих средств и инструментов; умение проводить классификацию объектов на основе критериев, выделять основное на фоне второстепенных данных; умение проводить логическое рассуждение в направлении от общих закономерностей изучаемой задачи до частных рассмотрений; умение строить логические рассуждения на основе системных сравнений основных компонентов изучаемого математического раздела или модели, понятия или классов, выделяя определенные существенные признаки или критерии; умение выявлять, строить закономерность, связность, логичность соответствующих цепочек рассуждений при работе с математическими задачами, уметь подробно и сжато представлять детализацию основных компонентов при доказательстве понятий и соотношений на математическом языке; умение организовывать поиск и выявлять причины возникающих процессов, явлений, наиболее вероятные факторы, по которым математические модели и объекты ведут себя по определенным логическим законам, уметь приводить причинно-следственный анализ понятий, суждений и математических законов; умение строить математическую модель при заданном условии, обладающей определенными характеристиками объекта при наличии определенных компонентов формирующегося предполагаемого понятия или явления; умение переводить текстовую структурно-смысловую составляющую математической задачи на язык графического отображения - составления математической модели, сохраняющей основные свойства и характеристики; умение задавать план решения математической задачи, реализовывать алгоритм действий как пошаговой инструкции для разрешения учебно-познавательной задачи; умение строить доказательство методом от противного; умение работать с проблемной ситуацией, осуществлять образовательный процесс посредством поиска методов и способов разрешения задачи, определять границы своего образовательного пространства; уметь ориентироваться в тексте, выявлять главное условие задачи и устанавливать соотношение рассматриваемых объектов; умение переводить, интерпретировать текст в иные формы представления информации: схемы, диаграммы, графическое представление данных; Коммуникативные УУД умение работать в команде, формирование навыков сотрудничества и учебного взаимодействия в условиях командной игры или иной формы взаимодействия; умение распределять роли и задачи в рамках занятия, формируя также навыки организаторского характера; умение оценивать правильность собственных действий, а также деятельности других участников команды; корректно, в рамках задач коммуникации, формулировать и отстаивать взгляды, аргументировать доводы, выводы, а также выдвигать контаргументы, необходимые для выявления ситуации успеха в решении той или иной математической задачи; умение пользоваться математическими терминами для решения учебно-познавательных задач, а также строить соответствующие речевые высказывания на математическом языке для выстраивания математической модели; уметь строить математические модели с помощью соответствующего программного обеспечения, сервисов свободного отдаленного доступа; уметь грамотно и четко, согласно правилам оформления КИМ-а ОГЭ заносить полученные результаты - ответы. В силу большой практической значимости данный курс представляет собой совокупность важных и полезных советов, знаний, является средством обучения и средством развития интеллектуальных качеств личности учащихся. Для учащихся, которые пока не проявляют заметного роста в плане математического усвоения основного содержания изучаемого предмета, эти занятия помогут стать толчком в развитии интереса к предмету и способствуют положительной тенденции в плане подготовки к основному государственному экзамену по математике. Результат обучения: формирование умений и навыков решения основных типовых задач основного государственного экзамена по математике, умение применять полученные знания на практике, в том числе планировать и проектировать свою деятельность с учетом конкретных жизненных ситуаций. Основное содержание Алгебра и арифметика Натуральные числа и нуль Натуральный ряд чисел и его свойства Натуральное число, множество натуральных чисел и его свойства, изображение натуральных чисел точками на числовой прямой. Использование свойств натуральных чисел при решении задач. Запись и чтение натуральных чисел Различие между цифрой и числом. Позиционная запись натурального числа, поместное значение цифры, разряды и классы, соотношение между двумя соседними разрядными единицами, чтение и запись натуральных чисел. Округление натуральных чисел Необходимость округления. Правило округления натуральных чисел. Сравнение натуральных чисел, сравнение с числом 0 Понятие о сравнении чисел, сравнение натуральных чисел друг с другом и с нулем, математическая запись сравнений, способы сравнения чисел. Действия с натуральными числами Сложение и вычитание, компоненты сложения и вычитания, связь между ними, нахождение суммы и разности, изменение суммы и разности при изменении компонентов сложения и вычитания. Умножение и деление, компоненты умножения и деления, связь между ними, умножение и сложение в столбик, деление уголком, проверка результата с помощью прикидки и обратного действия. Переместительный и сочетательный законы сложения и умножения, распределительный закон умножения относительно сложения, обоснование алгоритмов выполнения арифметических действий. Степень с натуральным показателем Запись числа в виде суммы разрядных слагаемых, порядок выполнения действий в выражениях, содержащих степень, вычисление значений выражений, содержащих степень. Дроби. Обыкновенные дроби Доля, часть, дробное число, дробь. Дробное число как результат деления. Правильные и неправильные дроби, смешанная дробь (смешанное число). Запись натурального числа в виде дроби с заданным знаменателем, преобразование смешанной дроби в неправильную дробь и наоборот. Приведение дробей к общему знаменателю. Сравнение обыкновенных дробей. Сложение и вычитание обыкновенных дробей. Умножение и деление обыкновенных дробей. Арифметические действия со смешанными дробями. Арифметические действия с дробными числами. Способы рационализации вычислений и их применение при выполнении действий. Десятичные дроби Целая и дробная части десятичной дроби. Преобразование десятичных дробей в обыкновенные. Сравнение десятичных дробей. Сложение и вычитание десятичных дробей. Округление десятичных дробей. Умножение и деление десятичных дробей. Преобразование обыкновенных дробей в десятичные дроби. Конечные и бесконечные десятичные дроби. Проценты Понятие процента. Вычисление процентов от числа и числа по известному проценту, выражение отношения в процентах. Решение несложных практических задач с процентами. Диаграммы Столбчатые и круговые диаграммы. Извлечение информации из диаграмм. Изображение диаграмм по числовым данным. Рациональные числа. Положительные и отрицательные числа Изображение чисел на числовой (координатной) прямой. Сравнение чисел. Модуль числа, геометрическая интерпретация модуля числа. Действия с положительными и отрицательными числами. Множество целых чисел. Понятие о рациональном числе. Первичное представление о множестве рациональных чисел. Действия с рациональными числами. Решение текстовых задач Единицы измерений: длины, площади, объема, массы, времени, скорости. Зависимости между единицами измерения каждой величины. Зависимости между величинами: скорость, время, расстояние; производительность, время, работа; цена, количество, стоимость. Квадратные корни Арифметический квадратный корень. Преобразование выражений, содержащих квадратные корни: умножение, деление, вынесение множителя из-под знака корня, внесение множителя под знак корня. Уравнения и неравенства Равенства Числовое равенство. Свойства числовых равенств. Равенство с переменной. Уравнения Понятие уравнения и корня уравнения. Представление о равносильности уравнений. Область определения уравнения (область допустимых значений переменной). Линейное уравнение и его корни Решение линейных уравнений. Линейное уравнение с параметром. Количество корней линейного уравнения. Решение линейных уравнений с параметром. Квадратное уравнение и его корни Квадратные уравнения. Неполные квадратные уравнения. Дискриминант квадратного уравнения. Формула корней квадратного уравнения. Теорема Виета. Теорема, обратная теореме Виета. Решение квадратных уравнений: использование формулы для нахождения корней, графический метод решения, разложение на множители, подбор корней с использованием теоремы Виета. Количество корней квадратного уравнения в зависимости от его дискриминанта. Биквадратные уравнения. Уравнения, сводимые к линейным и квадратным. Квадратные уравнения с параметром. Дробно-рациональные уравнения Решение простейших дробно-линейных уравнений. Решение дробно-рациональных уравнений. Методы решения уравнений: методы равносильных преобразований, метод замены переменной, графический метод. Использование свойств функций при решении уравнений. Простейшие иррациональные уравнения вида 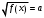 , ,  . .Уравнения вида 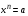 .Уравнения в целых числах. .Уравнения в целых числах.Системы уравнений Уравнение с двумя переменными. Линейное уравнение с двумя переменными. Прямая как графическая интерпретация линейного уравнения с двумя переменными. Понятие системы уравнений. Решение системы уравнений. Методы решения систем линейных уравнений с двумя переменными: графический метод, метод сложения, метод подстановки. Системы линейных уравнений с параметром. Неравенства Числовые неравенства. Свойства числовых неравенств. Проверка справедливости неравенств при заданных значениях переменных. Неравенство с переменной. Строгие и нестрогие неравенства. Область определения неравенства (область допустимых значений переменной). Решение линейных неравенств. Квадратное неравенство и его решения. Решение квадратных неравенств: использование свойств и графика квадратичной функции, метод интервалов. Запись решения квадратного неравенства. Решение целых и дробно-рациональных неравенств методом интервалов. |
