электив. Пояснительная записка Основной задачей обучения математике в школе является сознательное овладение учащимися системой математических знаний и умений, необходимых в повседневной жизни.

• Название: Пояснительная записка Основной задачей обучения математике в школе является сознательное овладение учащимися системой математических знаний и умений, необходимых в повседневной жизни.
• Анкор: электив
• Дата: 26.04.2022
• Размер: 0.71 Mb.
• Имя файла: электив.docx
• Тип: Элективный курс; #499400
• страница: 4 из 4

Степенная функция с показателем 3

Свойства. Кубическая парабола.

Функции 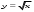, , 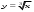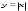.Их свойства и графики. Степенная функция с показателем степени больше 3.

Преобразование графиков функций: параллельный перенос, симметрия, растяжение/сжатие, отражение.

24. 
    Задачи-великаны
    

• 
  Отработка задач № 24 КИМ ОГЭ
  
• 
  Отработка задач № 25 КИМ ОГЭ
  
• 
  Отработка задач № 26 КИМ ОГЭ
  

Геометрические фигуры

Фигуры в геометрии и в окружающем мире

Геометрическая фигура. Внутренняя, внешняя области фигуры, граница. Линии и области на плоскости. Выпуклая и невыпуклая фигуры. Плоская и неплоская фигуры.

Выделение свойств объектов. Формирование представлений о метапредметном понятии «фигура». Точка, отрезок, прямая, луч, ломаная, плоскость, угол, биссектриса угла и ее свойства, виды углов, многоугольники, окружность и круг.

Осевая симметрия геометрических фигур. Центральная симметрия геометрических фигур.

Многоугольники

Многоугольник, его элементы и его свойства. Правильные многоугольники. Выпуклые и невыпуклые многоугольники. Сумма углов выпуклого многоугольника.

Треугольник. Сумма углов треугольника. Равнобедренный треугольник, свойства и признаки. Равносторонний треугольник. Медианы, биссектрисы, высоты треугольников. Замечательные точки в треугольнике. Неравенство треугольника.

Четырехугольники. Параллелограмм, ромб, прямоугольник, квадрат, трапеция. Свойства и признаки параллелограмма, ромба, прямоугольника, квадрата. Теорема Вариньона.

Окружность, круг

Их элементы и свойства. Хорды и секущие, их свойства. Касательные и их свойства. Центральные и вписанные углы. Вписанные и описанные окружности для треугольников. Вписанные и описанные окружности для четырехугольников. Вневписанные окружности. Радикальная ось.

Фигуры в пространстве (объемные тела)

Многогранник и его элементы. Названия многогранников с разным положением и количеством граней. Первичные представления о пирамидах, параллелепипедах, призмах, сфере, шаре, цилиндре, конусе, их элементах и простейших свойствах.

Отношения

Равенство фигур

Свойства и признаки равенства треугольников. Дополнительные признаки равенства треугольников. Признаки равенства параллелограммов.

Параллельность прямых

Признаки и свойства параллельных прямых. Аксиома параллельности Евклида. Первичные представления о неевклидовых геометриях. Теорема Фалеса.

Перпендикулярные прямые

Прямой угол. Перпендикуляр к прямой. Серединный перпендикуляр к отрезку. Свойства и признаки перпендикулярности прямых. Наклонные, проекции, их свойства.

Подобие

Пропорциональные отрезки, подобие фигур. Подобные треугольники. Признаки подобия треугольников. Отношение площадей подобных фигур.

Взаимное расположение прямой и окружности, двух окружностей.

Измерения и вычисления

Величины

Понятие величины. Длина. Измерение длины. Единцы измерения длины.

Величина угла. Градусная мера угла. Синус, косинус и тангенс острого угла прямоугольного треугольника.

Понятие о площади плоской фигуры и ее свойствах. Измерение площадей. Единицы измерения площади.

Представление об объеме пространственной фигуры и его свойствах. Измерение объема. Единицы измерения объемов.

Измерения и вычисления

Инструменты для измерений и построений; измерение и вычисление углов, длин (расстояний), площадей, вычисление элементов треугольников с использованием тригонометрических соотношений. Площади. Формулы площади треугольника, параллелограмма и его частных видов, трапеции, формула Герона, формула площади выпуклого четырехугольника, формулы длины окружности и площади круга. Площадь кругового сектора, кругового сегмента. Площадь правильного многоугольника.

Теорема Пифагора. Пифагоровы тройки. Тригонометрические соотношения в прямоугольном треугольнике. Тригонометрические функции тупого угла.

Теорема косинусов. Теорема синусов.

Решение треугольников. Вычисление углов. Вычисление высоты, медианы и биссектрисы треугольника.

Расстояния

Расстояние между точками. Расстояние от точки до прямой. Расстояние между фигурами.

Равновеликие и равносоставленные фигуры.

Свойства (аксиомы) длины отрезка, величины угла, площади и объема фигуры.

Геометрические построения

Геометрические построения для иллюстрации свойств геометрических фигур.

Инструменты для построений. Циркуль, линейка.

Простейшие построения циркулем и линейкой: построение биссектрисы угла, перпендикуляра к прямой, угла, равного данному.

Построение треугольников по трем сторонам, двум сторонам и углу между ними, стороне и двум прилежащим к ней углам, по другим элементам.

Деление отрезка в данном отношении.

Основные методы решения задач на построение (метод геометрических мест точек, метод параллельного переноса, метод симметрии, метод подобия).

Этапы решения задач на построение.

Геометрические преобразования

Преобразования

Представление о межпредметном понятии «преобразование». Преобразования в математике (в арифметике, алгебре, геометрические преобразования).

Движения

Осевая и центральная симметрии, поворот и параллельный перенос. Комбинации движений на плоскости и их свойства.

Подобие как преобразование

Гомотетия. Геометрические преобразования как средство доказательства утверждений и решения задач.

Векторы и координаты на плоскости

Векторы

Понятие вектора, действия над векторами, коллинеарные векторы, векторный базис, разложение вектора по базисным векторам. Единственность разложения векторов по базису, скалярное произведение и его свойства, использование векторов в физике.

Координаты

Основные понятия, координаты вектора, расстояние между точками. Координаты середины отрезка. Уравнения фигур.

Применение векторов и координат для решения геометрических задач.

Календарно-тематическое планирование

(составлено в соответствии с локальным актом МБОУ – Теляковской ООШ)

№ п/п	Дата		Название темы занятия	Кол-во часов	Характеристика деятельности обучающегося
	план	факт
1			Арифметические операции с дробями. Смешанные дроби, обыкновенные дроби, десятичные дроби.	1	Отработка навыков и умений решать задачи № 1 КИМ ОГЭ, содержащие дроби. Арифметические операции с дробями.
2			«Числовая прямая». Координаты на прямой. Расположение точек с координатами на прямой.	1	Отработка навыков и умений решать задачи на отыскание точек по координатам, на расположение и соответствие точек с задающими координатами.
3			Иррациональные числа. Избавления от иррациональности в знаменателе. Свойства корней. Арифметические операции с корнями.	1	Отработка навыков арифметических операций содержащих арифметический квадратный корень.
4			Решение линейных уравнений.	1	Отработка навыков решения уравнений относительно одной неизвестной.
5			Построение графиков различных функций. Определение знака углового коэффициента.	1	Отработка умений строить графики различных функций, определять знак углового коэффициента, формирование умений сопоставлять графику функции уравнение задающее множество точек. Отработка навыка построения функции по таблице значений x и y.
6			Арифметическая и геометрическая прогрессии.	1	Отработка навыков решения задач на определения n члена геометрической прогрессии, недостающего числа в ряду арифметической прогрессии, сумма геометрической и арифметической прогрессии.
7			Преобразование буквенных выражений. Выражения, содержащие формулы сокращенного умножения. Выделение полного квадрата. Многочлены. Деление углом.	1	Отработка навыков решения задач на преобразование буквенных выражений, сокращения, формулы сокращенного умножения.
8			Решение систем уравнений и неравенств.	1	Отработка навыков решения задач на решение систем уравнений и систем неравенств. Построение графиков функции. Решение системы графическим методом.
9			Задачи на отыскание значения угла в различных геометрических фигурах, находящихся в синтезе других геометрических объектов.	1	Отработка навыков решения геометрических задач на отыскание величины угла
10			Задачи на отыскание значения длины геометрического объекта, в различных геометрических фигурах.	1	Отработка навыков решения геометрических задач на отыскание длины геометрического элемента.
11			Задачи на нахождения площадей фигур с использованием известных формул.		Отработка навыков решения геометрических задач на отыскание площади геометрического объекта.
12			Задачи на нахождения площадей фигур с использованием известных формул, на фоне клеток 1х1.	1	Отработка навыков решения геометрических задач на отыскание площади геометрического объекта.
13			Теоретический марафон.	1	Создание на уроке кластеров или ментальной карты определений.
14			Анализ диаграмм, таблиц и схем.	1	Отработка на уроке навыков решения, анализа и генерация обсуждения текстовых задач с помощью составления диаграмм, таблиц данных или схем.
15			Анализ диаграмм, таблиц и схем. «Найди на графике». Отработка задач КИМ ОГЭ.	1	Отработка на уроке навыков решения и анализа текстовой задачи и определения стратегий ее решения на соответствующей иллюстрации, определяющей метод решения. Сопоставление условий задачи и ее интерпретации. Отыскание на графике элементов, удовлетворяющих решению.
16			Решение экономических задач на отыскание прибыли или скидки. Проценты. Доли.	1	Отработка навыков решения текстовых задач на отыскание скидки.
17			Решение текстовых задач по данным на диаграмме.	1	Отработка навыков решения практических задач на отыскание долей, процента или части значения от целого. Представление данных в схемах, диаграммах, таблицах.
18			Решение задач на диаграммы.	1	Отработка навыков решение на отыскание значений по диаграмме.
19			Решение задач на определения вероятности определенного события.	1	Отработка навыков решения задач на определения события. Отрицание. Классическое определение вероятности. Правило умножение.
20			Решение задач на выражение одних величин через известные. Сопоставление переменных задачи с 1соответствующим обозначением. Работа с формулой.	1	Отработка навыков решения задач на выявление неизвестных величин в формуле через известные.
21			Решение задач второй части. Уравнения различных степеней. Уравнения, содержащие корни, показательные уравнения, задачи с буквенными выражениями.	1	Отработка навыков решения задач на отыскание корня уравнения, переменной, выражения.
22			Решение текстовых задач на движение.	1	Решение задач на отработку текстовых задач на движение, на работу..
23			Решение текстовых задач на работу.	1
24			Решение задач на построение графиков функций различных видов.	1	Решение задач на отработку задач на построение графиков функций и его свойств, исследование графика функции.
25			Исследование графиков функции	1
26			Кусочно – непрерывные функции.	1
27			Параболы.	1
28			Гиперболы.	1
29			Геометрическая задача на вычисление.	1	Решение задач на отыскание геометрических компонентов. Задачи на дополнительные построение, на использование геометрического аппарата формул, теорем и доказательства. Самостоятельная работа
30			Комбинация многоугольников и окружностей.	1
31			Геометрическая задача повышенной сложности.	1
32			Сложная задача по геометрии.	1
33-34			Написание тренировочного варианта	2

Примерный вариант итоговой работы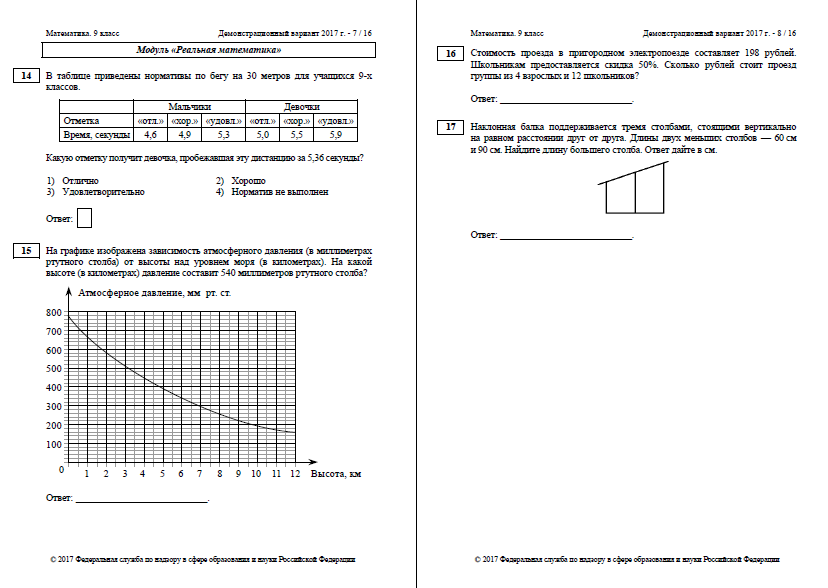