Практикум_по_математике_Заикина. Пояснительная записка Требование современного общества к образованию предоставление возможности школьнику выстраивать индивидуальные образовательные маршруты, удовлетворяющие интересы и потребности каждой личности.
 Скачать 59 Kb. Скачать 59 Kb.
|
|
Задание 5. Существует ли такой выпуклый многоугольник, которого отношение суммы внутренних углов к сумме внешних (взятых по одному при каждой вершине) равно 15 : 4? Решение. Сумма внутренних углов многоугольника 180º (n – 2), а сумма внешних углов 360º. Значит, 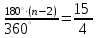 , ,откуда n=9,5. Число сторон не может быть дробным, значит, такой многоугольник не существует. Задание 6. Основания трапеции равны 3 см и 2 см. Диагонали её равны 4 см и 3 см. Найдите площадь трапеции. Решение. Пусть дана трапеция ABCD. Проведём ED ║ AC до пересечения с продолжением ВС в точке Е. В треугольнике BED стороны равны 3 см, 4 см и 5 см, значит, угол BDE-прямой, поэтому и угол АОD-прямой, т. е. диагонали трапеции взаимно перпендикулярны. SABCD = 0,5 AC ∙ BD = 6(см2). Задание 7. Натуральные числа а, b и с таковы, что аb + bс = са. Докажите равенство НОД(а, b) + НОД(b, с) = НОД(с, а). (Здесь НОД – наибольший общий делитель.) Доказательство. Задача легко сводится к случаю, когда числа а,в и с не имеют общего делителя. В этом случае НОД(а, b) = 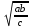 , НОД(b, с) = , НОД(b, с) = 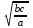 и НОД(а, с) = и НОД(а, с) = 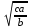 . Равенство . Равенство 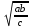 + + 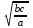 = = 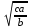 справедливо, так как после умножения его на справедливо, так как после умножения его на 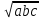 получим верное равенство ab + bc = ca. получим верное равенство ab + bc = ca.Задание 8. Докажите, что число 1991 · 1993 · 1995 · 1997 + 16 является квадратом натурального числа. Доказательство. Имеет место тождество (n – 3)(n – 1)(n + 1)(n +3) + 16 = (n2 – 5)2. Отсюда следует числовое равенство 1991 · 1993 · 1995 · 1997 + 16 = (19942 – 5)2. Задание 9. Целые числа a, b c таковы, что ab + bc + ca = 0. Докажите, что число abc может быть представлено в виде произведения квадрата целого числа на куб целого числа. Доказательство. Покажем, что если числа a, b, и c не имеют общего делителя, то число abc является полным квадратом. Пусть p – простое число и с делится на pn, тогда из равенства ab = - c(a + b) следует, что одно из чисел a и b делится на pn, а второе не делится на p; значит, abc делится на p2n. Аналогично рассуждая про делители чисел а и b, получаем, что любое простое число входит в произведение abc в четвёртой степени. Если у чисел a, b, c есть общий делитель, то он войдёт в произведение в кубе. Задание 10. Существует ли такое двузначное число, которое при делении на произведение его цифр даёт в частном 4 и в остатке 6? Решение. Предположим, что такое число существует. Обозначив через x и y соответственно число его десятков и число единиц, получим для определения неизвестных уравнение 10x + y = 4xy + 6 (1) и неравенство xy > 6, (2) поскольку остаток меньше делителя. Так как уравнение (1) равносильно уравнению (4x – 1)(5 – 2y) = 7 ∙ 1 (3) и x – натуральное число, то 4x – 1 > 1. Следовательно, из (3) с учётом того, что y - число целое, имеем: 4x – 1 = 7 и 5 – 2y = 1, т. е. x = 2, y = 2, но эта пара чисел не удовлетворяет неравенству (2). Итак, не существует двузначное число, которое при делении на произведение его цифр даёт в частном 4 и в остатке 6. Список литературы 1. Н.А. Криволапова «Внеурочная деятельность. Программа развития познавательных способностей учащихся».М. «Просвещение».2018 Н.А. Криволапова «Внеурочная деятельность. Сборник заданий для развития познавательных способностей учащихся5-8 классы». М. «Просвещение». 2017 А.Р.Рязановский, Д.Г. Мухин «Математика. ОГЭ. Теория вероятностей и элементы статистики». М.«Экзамен»2017 Я.И. Перельман «Занимательная арифметика». М. Изд. «Астрель» 2017 Я.И. Перельман «Занимательная геометрия».М. Изд. «Астрель» 2012 Я.И. Перельман «Живая математика». М. Изд. «Наука», 1974г |
