Практическая работа 1 Задачи на комплексные числа в алгебраической, тригонометрической и показательной формах
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
1 2 Практическая работа №1 Задачи на комплексные числа в алгебраической, тригонометрической и показательной формах Даны комплексные числа вычислить сумму 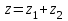 аналитически и графически, найти модуль и аргумент z, а так же аналитически и графически, найти модуль и аргумент z, а так же 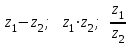 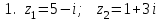 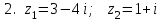 2 Выполнить действия над комплексными числами в тригонометрической форме, результат записать в тригонометрической, алгебраической и показательной форме 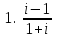 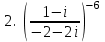 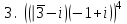 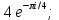 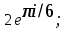 3. Выполнить действия. Результат записать во всех формах. 1. 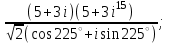 2. 2. 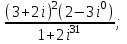 4. Выполнить действия, используя тригонометрическую форму: 1. 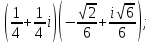 2. 2.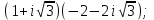 5. Выполнить действия над комплексными числами в тригонометрической форме: 1) 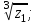 2) 2) 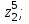 1. 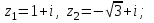 2.  Вариант 2 Выполнить действия и записать результат в тригонометрической форме: а) 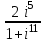 ; б) ; б) 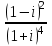 . .Выполнить действия и записать результат в показательной форме: а) 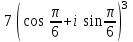 ; б) ; б) 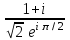 . .Составить квадратное уравнение по его корням 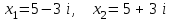 Выполнить действия: 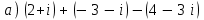  Построить слагаемые 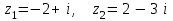 и их сумму. и их сумму.Выполнить действия: 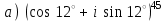 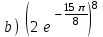 Выполнить действия и записать результат в показательной форме: 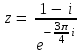 Выполнить действия над комплексными числами: 1) 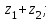 2) 2) 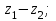 3) 3) 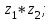 4) 4) 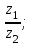 Даны комплексные числа вычислить сумму 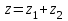 аналитически и графически, найти модуль и аргумент z, а так же аналитически и графически, найти модуль и аргумент z, а так же 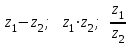 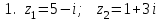 Вариант 3 Выполнить действия и записать результат в тригонометрической форме: а) 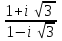 ; б) ; б) 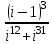 . .Выполнить действия и записать результат в показательной форме: а) 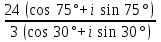 ; б) ; б) 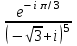 . .Решить квадратное уравнение  Выполнить действия: 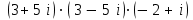 Построить комплексные числа 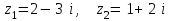 , а также им сопряженные и противоположные. , а также им сопряженные и противоположные.Выполнить действия: 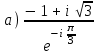 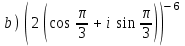 Выполнить действия и записать результат в показательной форме: 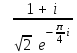 Даны комплексные числа вычислить сумму 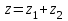 аналитически и графически, найти модуль и аргумент z, а так же аналитически и графически, найти модуль и аргумент z, а так же 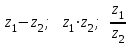 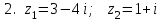 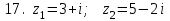 Выполнить действия и записать результат в тригонометрической форме: а) 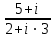 ; б) ; б) 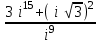 . .Выполнить действия и записать результат в показательной форме: а) 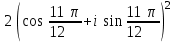 ; б) ; б) 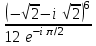 . .2. Выполнить действия над комплексными числами в алгебраической форме 1) 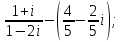 2) 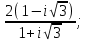 3) 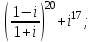 Даны комплексные числа вычислить сумму 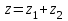 аналитически и графически, найти модуль и аргумент z, а так же аналитически и графически, найти модуль и аргумент z, а так же 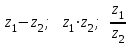 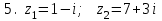 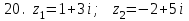 Вариант 5 Выполнить действия и записать результат в тригонометрической форме: а) 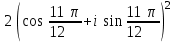 ; б) ; б) 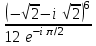 . .Выполнить действия и записать результат в показательной форме: а) 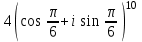 ; б) ; б) 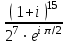 . .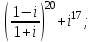 4) 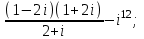 5) 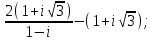 6) 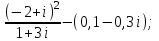 Даны комплексные числа вычислить сумму 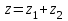 аналитически и графически, найти модуль и аргумент z, а так же аналитически и графически, найти модуль и аргумент z, а так же 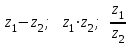 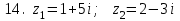 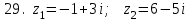 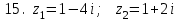 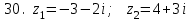 Вариант 6 Выполнить действия и записать результат в тригонометрической форме: а) 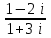 ; б) ; б) 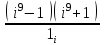 . .Выполнить действия и записать результат в показательной форме: а) 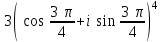 ; б) ; б) 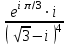 . .Выполнить действия над комплексными числами в алгебраической форме 1 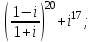 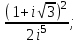 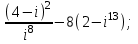 Выполнить действия над комплексными числами: 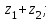 2) 2) 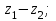 3) 3)  4) 4)    5Даны комплексные числа вычислить сумму  аналитически и графически, найти модуль и аргумент z, а так же аналитически и графически, найти модуль и аргумент z, а так же 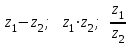 6 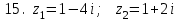 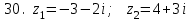 7 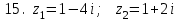 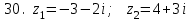 Практическая работа №2 Вычисление определителей 2 и 3 порядка Систему уравнений записать в матричной форме и решить: а) с помощью обратной матрицы, б) с помощью правила Крамера и в) методом Гаусса. Вариант№1 1. 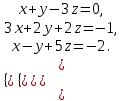 Вариант 2. Вариант 2. 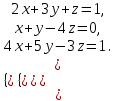 Вариант№2 3. 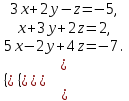 Вариант 4. Вариант 4. 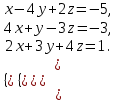 Вариант№3 5. 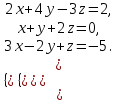 6. 6. 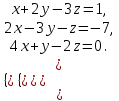 Вариант№4 7. Вариант№4 7. 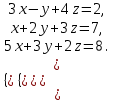 Вариант 8. Вариант 8.  Контрольная работа по теме Решение систем уравнений Вариант 1 Решить систему уравнений по формулам Крамера 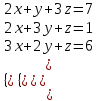 Решить систему уравнений по формулам методом Гаусса а) 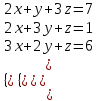 б) б) 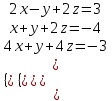 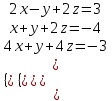 Вариант 2 Найти матрицу C=2A-B, если 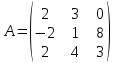 , , 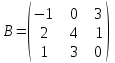 . .Ответ: 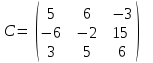 Решить систему линейных уравнений по формулам Крамера. Решить систему линейных уравнений методом Гаусса. 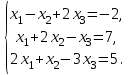 Ответ: (1;3;0) Вариант 3 Найти матрицу C=3A+B, если 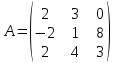 , , 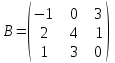 . .Ответ: 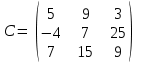 Решить систему линейных уравнений по формулам Крамера. Решить систему линейных уравнений методом Гаусса. 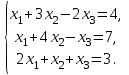 Ответ: (0;2;1) Вариант 4 Найти матрицу C=A-4B, если 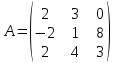 , , 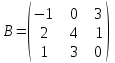 . .Ответ: 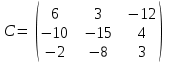 Решить систему линейных уравнений по формулам Крамера. Решить систему линейных уравнений методом Гаусса. 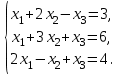 Ответ: (2;1;1) Вариант 5 Найти матрицу C=4A-B, если 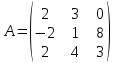 , , 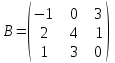 . .Ответ: 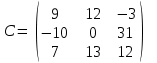 Решить систему линейных уравнений по формулам Крамера. Решить систему линейных уравнений методом Гаусса. 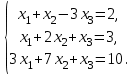 Ответ: (1;1;0) Вариант 6 Найти матрицу C=A+2B, если 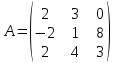 , , 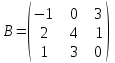 . .Ответ: 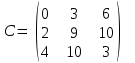 Решить систему линейных уравнений по формулам Крамера. Решить систему линейных уравнений методом Гаусса. 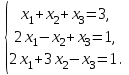 Ответ: (0;1;2) . Практическая работа№3.Вычисление пределов с помощью формул первого и второго замечательных пределов. Вычисление пределов функции с помощью раскрытия неопределённостей. Вариант 1 Вычислить предел функции: 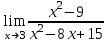 . .Вычислить предел функции:  . .Вычислить предел функции: 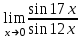 . .Вычислить предел функции: 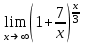 . .Вариант 2 Вычислить предел функции: 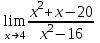 . . Вычислить предел функции: 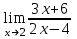 . .Вычислить предел функции: 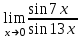 . .Вычислить предел функции: 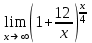 . .Вариант 3 Вычислить предел функции: 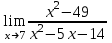 . .Вычислить предел функции: 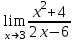 . .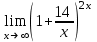 Вычислить предел функции: 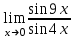 . .Вычислить предел функции: 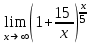 . .Вариант 4 Вычислить предел функции: 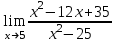 . .Вычислить предел функции: 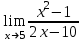 . .Вычислить предел функции: 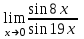 . .Вычислить предел функции: 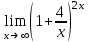 . .Вариант 5 Вычислить предел функции: 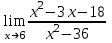 . .Вычислить предел функции: 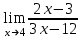 . .Вычислить предел функции: 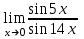 . .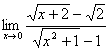 Вычислить предел функции: 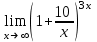 . .Вариант 6 Вычислить предел функции:  . .Вычислить предел функции: 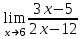 . .Вычислить предел функции: 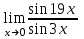 . .Дополнительное задание а) 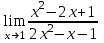 ; б) ; б)  ; ;в) 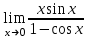 ; г) ; г) 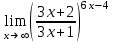 . .8. а) 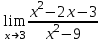 ; б) ; б)  ; ;в) 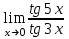 ; г) ; г) 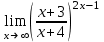 . .9. а) 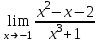 ; б) ; б) 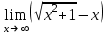 ; ;в) 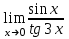 ; г) ; г) 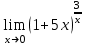 . .10. а)  ; б) ; б) 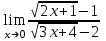 ; ;в) 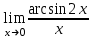 ; г) ; г) 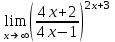 . .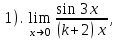  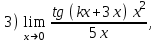 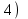 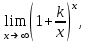 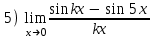 , , 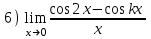 7) 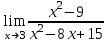 8) 8) 9) 9) 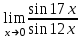 10) 10)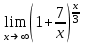 Найти указанные пределы. 1. а) 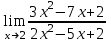 ; б) ; б) 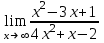 ; ;в) 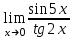 ; г) ; г) 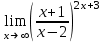 . .2. а) 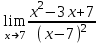 ; б) ; б) 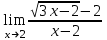 ; ;в)  ; г) ; г) 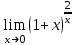 . .3. а) 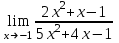 ; б) ; б) 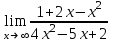 ; ;в)  ; г) ; г) 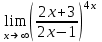 . .4. а) 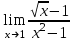 ; б) ; б)  ; ;в)  ; г) ; г)  . .5. а)  ; б) ; б) 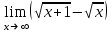 ; ;в)  ; г) ; г) 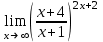 . .6. а) 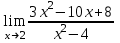 ; б) ; б) 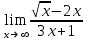 ; ;в) 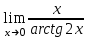 ; г) ; г) 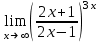 . .д) Практическая работа №3 Вычисление производной функции. Найти главное приращение функции dy 1 вариант у = х2 + cos 3x – 5 2 вариант y = cos (1- x2) 3 вариант у = (1 – х2)5 4 вариант у = (2х2 – 5)3 5 вариант у = 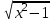 6 вариант у = 6 вариант у = 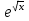 7 вариант у = 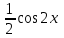 8 вариант у = 8 вариант у = 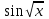 9 вариант 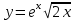 10 вариант 10 вариант 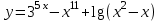 Найти производную по её определению (через предел) 1 вариант у = 2х2 – 3х 2 вариант у = 2х3 3 вариант у = х3 + х 4 вариант у = 5х2 - х 5 вариант у = 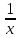 6 вариант у = 6 – х – х2 6 вариант у = 6 – х – х27 вариант у = 2 – х2 8 вариант у = х2 + 4х 9 вариант у = х2 – х 10 вариант у = х2 + 2х Найти производные, используя таблицу и правила дифференцирования 1 вариант а) y = 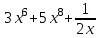 б) y = б) y =  в) y = 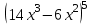 г) y = г) y = 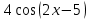 д) y = д) y =  2 вариант а) у = 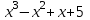 б) у = б) у = 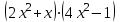 в) у = 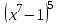 г) у = г) у = 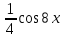 д) у = д) у =  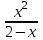 Найти производные, используя таблицу и правила дифференцирования 1 вариант а) y = 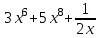 б) y = б) y =  в) y = 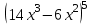 г) y = г) y = 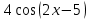 д) y = д) y =  2 вариант а) у = 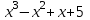 б) у = б) у = 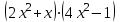 в) у = 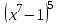 г) у = г) у = 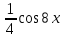 д) у = д) у =   3 вариант а)  б) б)  в)  г) г)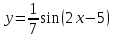 д) д) 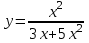 4 вариант а) 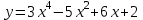 б) б) 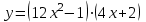 в) 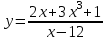 г) г) 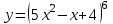 д) д) 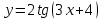 5 вариант а) 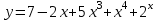 б) б) 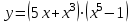 в) 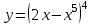 г) г) 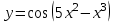 д) д) 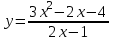 6 вариант а) 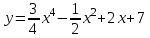 б) б) 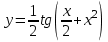 в) 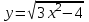 г) г) 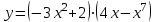 д) д) 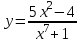 7 вариант а) 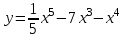 б) б) 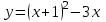 в) 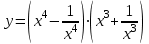 г) г)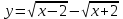 д) 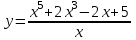 8 вариант а) 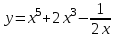 б) б) 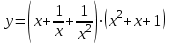 в) 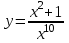 г) г) 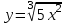 д) д) 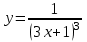 9 вариант а) 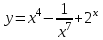 б) б)  в)  г) г)  д) д)  10 вариант а) 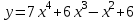 б) б) 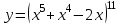 в) 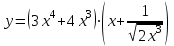 г) г) 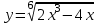 д) д) 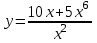 Практическая работа №4 Производная сложной функции Вариант 1 1. Найдите производную функции у = 0,5sin2x +5х –cos2x +5; 2) cos2x +5; 3) 0,5cos2x +5; 4) –0,5sin2x + 5. 2. Угловой коэффициент наклона касательной к графику функции у = 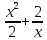 в точке х = – 1 равен в точке х = – 1 равен– 3; 2) – 2; 3) – 1,5; 4) 0. 3. Производная функции у = 2cosx – 3х2 в точке х0 = 0 равна 2; 2) – 3; 3) 0; 4) – 6. 4. В какой точке графика функции у = х2 – 3х + 5 тангенс угла наклона касательной равен 1 (0; 5); 2) (1; 3); 3) (–1; 9); 4) (2; 3). 5. При движении тела по прямой расстояние s (в км) от начальной точки меняется по закону s(t)=  + 2 (t – время движения в часах). Найдите скорость (в км/ч) тела через 1 час после начала + 2 (t – время движения в часах). Найдите скорость (в км/ч) тела через 1 час после начала движения. 2; 2) 0,1; 3) 1,5; 4) 0,5. 1 2 |
