Практическая работа. Математика. Практическая работа Приближённое значение. Абсолютная и относительная погрешности
 Скачать 0.85 Mb. Скачать 0.85 Mb.
|
|
Пример . Найти скалярное произведение векторов Решение: Здесь векторы a и b заданы как суммы базисных векторов (в ортонормированном базисе), т.е. они имеют координаты Известны их координаты, поэтому для вычисления скалярного произведения применим формулу (стрелочки над векторами ставить не будем, как и в большинстве задачников, но, вообще говоря, они должны быть). Подставим: Ответ: 13. Пример . Найти угол между векторами Решение: Применим формулу 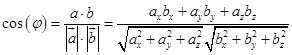 Подставим 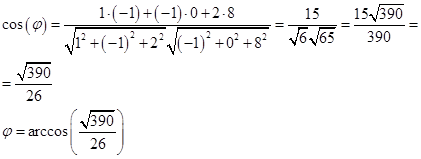 Ответ: 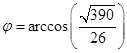 Задания. 1. Найдите: а) длину вектора 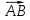 , если точка А(3;-1;5) и В(2;3;-4) , если точка А(3;-1;5) и В(2;3;-4)б) скалярное произведение векторов 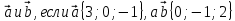 2. Найдите: a) длину 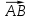 , если А(-1;0;2) и В(1;-2;3) , если А(-1;0;2) и В(1;-2;3)б) скалярное произведение векторов 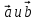 , если , если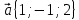 и и 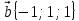 3. Найдите: a) длину 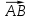 , если А(-35;-17;20) и В(-34;-5;8) , если А(-35;-17;20) и В(-34;-5;8)б) скалярное произведение векторов 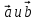 , если , если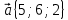 и и 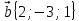 4. Когда скалярное произведение ненулевых векторов равно нулю? 5. Вычислить скалярное произведение 6. Вычислить скалярное произведение 7. Дан куб АBCDА1B1C1D1, введена система координат, как показано на рисунке. Найдите: 1   . координаты вектора АВ и вектора АС; . координаты вектора АВ и вектора АС; 2. Как будет выглядить формула вычисления скалярного произведения в пространстве? 3     . Найдите AB * АC. (ответы: 1. {-1;0;1}, {-1;1:0}2. a * b = х1 х2+у1у2+z1z2 . Найдите AB * АC. (ответы: 1. {-1;0;1}, {-1;1:0}2. a * b = х1 х2+у1у2+z1z2 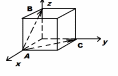 8. Найти длину вектора  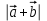 , если , если 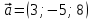 и и  9. Вычислить скалярное произведение векторов  ,, если ,, если  , ,  10. Найти косинус угла между векторами  и и  , если , если  , ,  |
