Практическая работа. Математика. Практическая работа Приближённое значение. Абсолютная и относительная погрешности
 Скачать 0.85 Mb. Скачать 0.85 Mb.
|
|
Логарифмические уравнения и неравенства. ЦЕЛЬ: закрепить навыки решения логарифмических уравнений и неравенств. Перед выполнением практической работы необходимо повторить основные методы решения логарифмических уравнений и неравенств. Учебный элемент № 1 Цель: закрепить решение простейших логарифмических уравнений вида 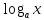 =в (где а >0, а ≠1). =в (где а >0, а ≠1).Рекомендации к выполнению: Вспомните определение логарифма. Повторите схему решения логарифмических уравнений вида 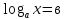 Логарифмическая функция возрастает (или убывает) на промежутке ( 0; +∞) и принимает на этом промежутке все действительные значения. По теореме о корне для любого в данное уравнение имеет единственное решение. Из определения логарифма следует, что ав является таким решением. Пример: решите уравнение 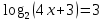 Решение: 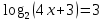 4х +3 = 23 4х = 8-3 4х = 5 х =1 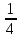 Ответ: 1 Ответ: 1 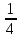 Выполните письменную самостоятельную работу (15 мин)
Учебный элемент № 2 Цель: закрепить умения решать логарифмические уравнения методом введения новой переменной. Рекомендации к выполнению: Внимательно разберите решение примера и выполните задания самостоятельной работы. Пример. Решите уравнение 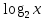 - -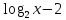 =0 =0Решение: Введем новую переменную t, t= 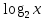 , тогда уравнение примет вид t2 –t -2 = 0 , тогда уравнение примет вид t2 –t -2 = 0 D = (-1)2 -4∙ 1 (-2) = 9 t1 = 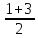 = 2 ; = 2 ; 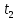 = =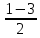 = -1 = -1Если t = 1 тогда: 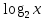 = -1, х = 2 -1, х = = -1, х = 2 -1, х =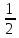 Если t =2, тогда: 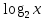 = 2, х = 22, х =4 Ответ: = 2, х = 22, х =4 Ответ: 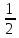 ; 4 ; 4Выполните письменную самостоятельную работу (10 мин)
Учебный элемент № 3 Цель: закрепить навыки решения логарифмических уравнений вида 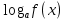 = = 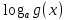 Рекомендации к выполнению: Помните, что решение таких уравнений основано на том, что такое уравнение равносильно уравнению f(x) =g(x) при дополнительных условиях f(x) > 0 ,g(x) > 0. Можно при решении таких уравнений использовать следующую схему: 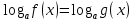 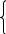 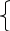 f(x) =g(x) f(x) = g (x) f(x) > 0 или g(x) > 0 Внимательно разберите данные ниже решения и выполните задания самостоятельной работы. П 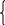 ример: Решите уравнения. ример: Решите уравнения. 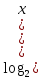 -3х + 1) = -3х + 1) =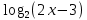 х2- 3х +1 = 2х -3, 2х – 3 >0; Решим уравнение х2 -3х + 1 = 2х – 3 х2 – 3х + 1 – 2х + 3 = 0 х2 - 5х +4 = 0 D= 25 -16 = 9 х1 = 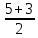 = 4, х2 = = 4, х2 =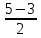 = 1 = 1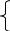 x = 4 или х = 1 x > 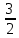 х = 4 Ответ : 4. Пример: Решите уравнение Lg(x2 +75) – Lg (x -4) =2 Решение: Lg(x2 +75) –Lg(x-4) = 2 Н  айдем ОДЗ : х2 +75 > 0 айдем ОДЗ : х2 +75 > 0x-4 > 0  x –любое число х > 4 ОДЗ: ( 4; +∞) Lg(x2 +75)=2 + Lg (х-4) Lg (x2 +75) = Lg 100 +Lg (x-4) Lg (x2 +75) = Lg (100x – 400) x2 +75 = 100x – 400 x2 -100x +75 +400 =0 x2 -100x +475 = 0 D = 1002 – 4 1 475 = 100 000 – 1900 = 8100 x1 = 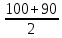 =95 =95x2 = 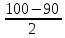 = 5 95 и 5 входят в ОДЗ = 5 95 и 5 входят в ОДЗОтвет: 95; 5. Выполните самостоятельную работу
Учебный элемент № 4 Цель: закрепить умения решать простейшие логарифмические неравенства. Рекомендации к выполнению: Решение логарифмических неравенств основано на том, что функция у = 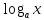 при а>1 является монотонно возрастающей на своей области определения, а при 0 при а>1 является монотонно возрастающей на своей области определения, а при 0При переходе от простейшего неравенства к равносильным системам неравенств, не содержащих знака логарифма следует учитывать область допустимых значений исходного неравенства. При решении логарифмических неравенств пользуйтесь следующей схемой:
Пример: 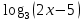 < 2 < 2Решение: 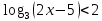 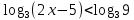 Функция у = 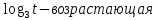 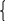 2х-5< 9 2х-5< 92х-5 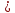 0; 0;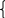 2х <14 2х <142х >5;  х <7 х>2,5 х 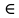 (2,5; 7) (2,5; 7)Ответ: х 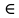 (2,5; 7) (2,5; 7)Выполните письменную самостоятельную работу
Учебный элемент № 5 Цель: закрепить умение решать логарифмические неравенства с использованием свойств логарифмов. Рекомендации к выполнению: Внимательно рассмотрите решение примеров и выполните задания самостоятельной работы. Пример: Найдите наибольшее целое решение неравенства: 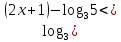 0 0Решение: 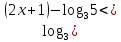 0 0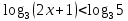 Так как основания логарифмов одинаковы и больше 1, то последнее неравенство равносильно системе неравенств: 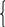 2х+1 2х+1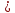 0, 0,2х +1 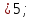 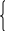 2х 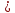 - 1, - 1,2х 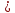 4; 4;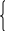 х 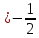 , ,х 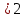 . х . х 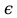 (- (-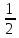 ; 2) ; 2)Т.к. число 2 данному промежутку не принадлежит, то наибольшее целое значение х равно 1. Ответ: 1. Выполните письменную самостоятельную работу
Практическая работа Расстояние от точки до плоскости, от прямой до плоскости, расстояние между плоскостями, между скрещивающимися прямыми. ЦЕЛЬ: обобщить, систематизировать изученное по данной теме, определить уровень усвоения знаний, оценить результаты деятельности обучающихся.    Практическая работа Скалярное приведение векторов в пространстве. ЦЕЛЬ: закрепить знания и умения выполнять действия над векторами, находить скалярное произведение векторов. Для выполнения заданий по данной теме необходимо предварительно изучить теоретические материалы, а также методические рекомендации к выполнению работы Краткие теоретические сведения Вектором называется отрезок, у которого указано, какой из концов является началом, а какой – концом (направленный отрезок), обозначается 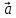 , , 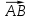 , где , где 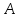 - начало вектора, - начало вектора, 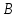 - конец. - конец.Модуль вектора 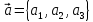 равен равен 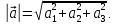 Скалярным произведением векторов называется число, равное произведению длин этих векторов на косинус угла между ними 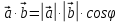 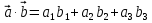 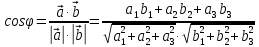 |

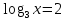 (1 б)
(1 б)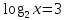 (1 б)
(1 б)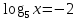 ( 1б)
( 1б)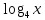 = -2 (1 б)
= -2 (1 б)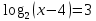 (1 б)
(1 б)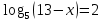 (1 б)
(1 б)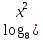 -1) = 1 (1 б)
-1) = 1 (1 б)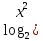 -1) = 3 (2 б)
-1) = 3 (2 б)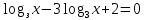 (2 б)
(2 б)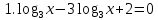 (2 б)
(2 б)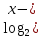 .
.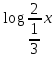 -
- 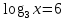 (2б)
(2б)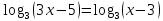 (2 б)
(2 б)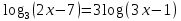 (2 б)
(2 б)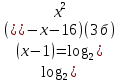
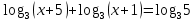 (4 б)
(4 б)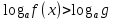 (x)
(x)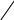
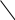
 f(x) > g(x) f(x) < g(x)
f(x) > g(x) f(x) < g(x)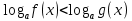

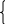 (x) < g(x) f(x) > g(x)
(x) < g(x) f(x) > g(x)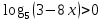 (1 б)
(1 б)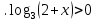 (1б)
(1б)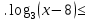 1 (1 б)
1 (1 б)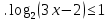 (1 б)
(1 б)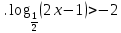 (1 б)
(1 б)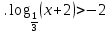 (1 б)
(1 б)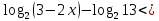 0 (2б)
0 (2б)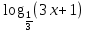 -
-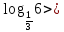 0 (2б)
0 (2б)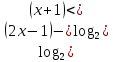 0 (3б)
0 (3б)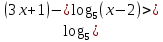 0 (3б)
0 (3б)