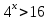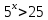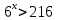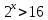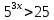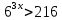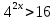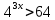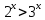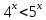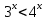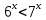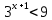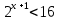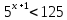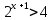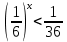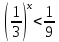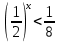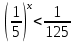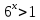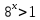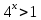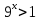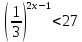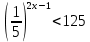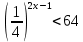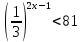Практическая работа. Математика. Практическая работа Приближённое значение. Абсолютная и относительная погрешности
 Скачать 0.85 Mb. Скачать 0.85 Mb.
|
|
Тема 3. Прямые и плоскости в пространстве Практическая работа Расстояние от точки до плоскости, от прямой до плоскости, расстояние между плоскостями, между скрещивающимися прямыми. Практическая работа Степенная функция. Преобразование графиков степенной функции. ЦЕЛЬ: повторить правила построения графика функции у = х р, при различных значениях р, научиться применять приемы преобразования графиков, демонстрировать применение свойств степенной функции при сравнении значений выражений, а также решение простейших уравнений и неравенств.  Степенная функция у = хр р - заданное действительное число 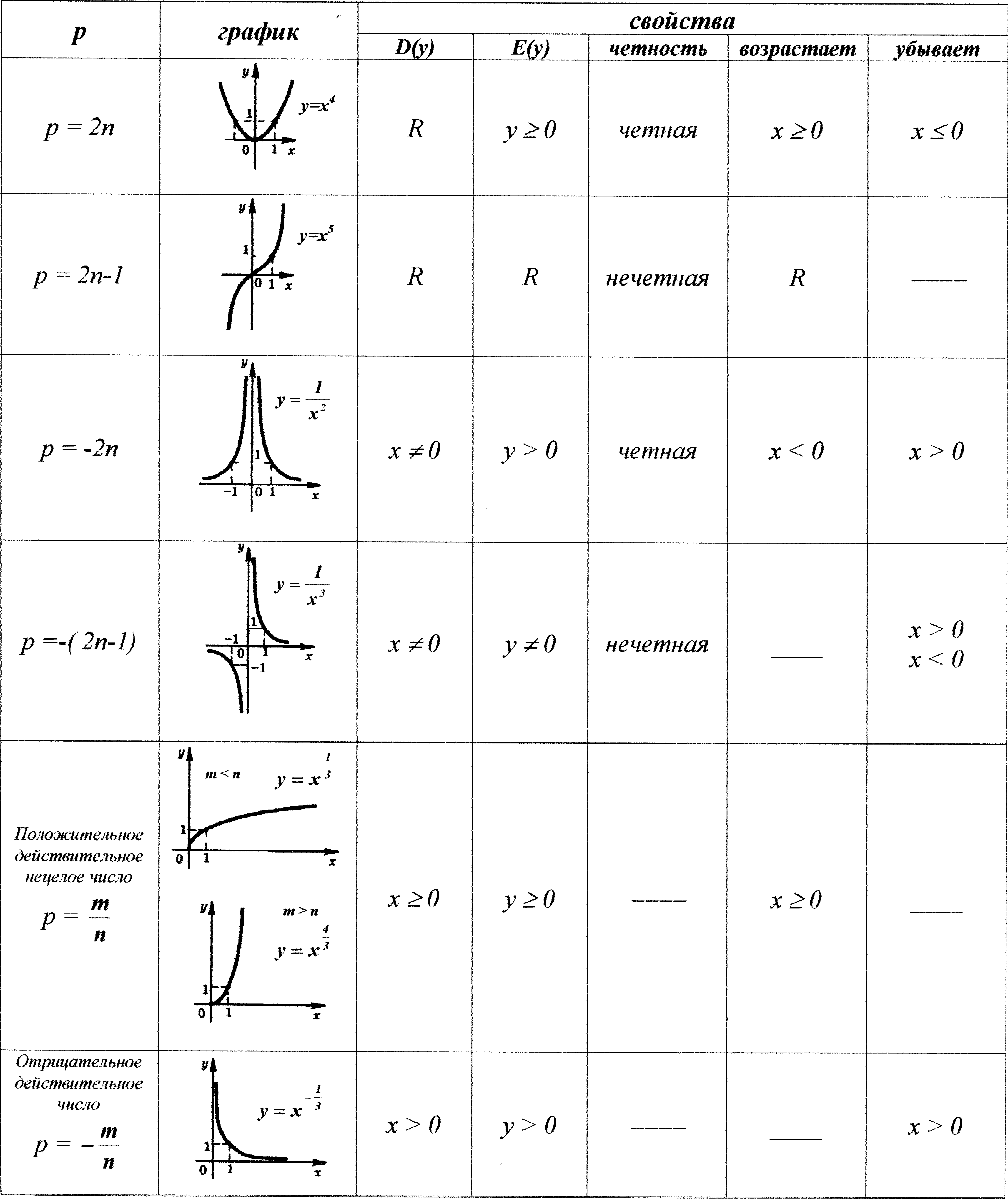 Степенная функция у = хр р - заданное действительное число  Выполнить самостоятельно Вариант 1 Уровень 1 А)В одной системе координат построить графики функции у=х3 и у=х1/3 Б)Найти область определения и множество значений для каждой функции. В) С помощью графиков решить уравнение х3 = х1/3 С) С помощью графиков решить неравенство х3< х1/3 Уровень 2 Изобразить схематически график функции у = хП+1 Наитии область определении и множество значений функции. Определить возрастает или убывает функция. Уровень 3 Построить график функции и указать область определения, множество значений и промежутки возрастания и убывания функции: у =│х│1/3 Вариант 2 Уровень 1 А)В одной системе координат построить графики функции у = х2 и у = х -2 Б)Найти область определения и множество значений для каждой функции. В) С помощью графиков решить уравнение х2 = х-2 С) С помощью графиков решить неравенство х2 > х -2 Уровень 2 Изобразить схематически график функции 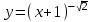 Наитии область определении и множество значений функции. Определить возрастает или убывает функция. Уровень 3 Построить график функции и указать область определения, множество значений и промежутки возрастания и убывания функции: у =│х│5 Вариант 3 Уровень 1 А)В одной системе координат построить графики функции у = х4 и у = х 1/4 Б)Найти область определения и множество значений для каждой функции. В) С помощью графиков решить уравнение х4 = х1/4 С) С помощью графиков решить неравенство х4 > х 1/4 Уровень 2 Изобразить схематически график функции 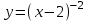 Наитии область определении и множество значений функции. Определить возрастает или убывает функция. Уровень 3 Построить график функции и указать область определения, множество значений и промежутки возрастания и убывания функции: у =│х│3+1 Вариант 4 Уровень 1 А)В одной системе координат построить графики функции у = х5 и у = х -5 Б)Найти область определения и множество значений для каждой функции. В) С помощью графиков решить уравнение х5 = х-5 С) С помощью графиков решить неравенство х5 < х -5 Уровень 2 Изобразить схематически график функции 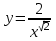 Наитии область определении и множество значений функции. Определить возрастает или убывает функция. Уровень 3 Построить график функции и указать область определения, множество значений и промежутки возрастания и убывания функции: у =│х+2│1/3 Практическая работа Логарифмы и их свойства. Правила логарифмирования. ЦЕЛЬ: способствовать формированию умения применять свойства логарифмов при решении заданий Определение: Логарифмом положительного числа b по основанию называется показатель степени с, в которую надо возвести число а, чтобы получить число b. 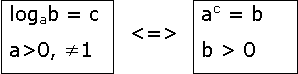 Основное логарифмическое тождество: 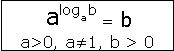 Свойства логарифмов: 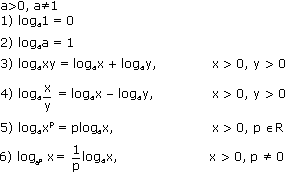 7) Формула перехода к новому основанию: Десятичный логарифм: lga = log10a Натуральный логарифм: lna = logea, e ≈ 2,718… I вариант 1. Найдите х: 1) log3 x = -2; 2) log36 x = 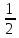 ; 3) log3 x = 3; ; 3) log3 x = 3; 4) log64 4 = x; 5) log3 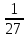 = x; 6) log2 16 = x; = x; 6) log2 16 = x; 7) logx 16 = 2; 8) logx 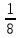 = -3; 9) logx 5 = = -3; 9) logx 5 = 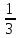 . . 10) log2 x = -3; 11) log49 x = 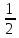 ; 12) log2 x = 3; ; 12) log2 x = 3; 13) log625 5 = x; 14) log2 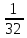 = x; 15) log3 27 = x; = x; 15) log3 27 = x; 16) logx 25 = 2; 17) logx 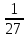 = -3; 18) logx 4 = = -3; 18) logx 4 = 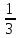 . . 2. Вычислите: 1) log49 + 2 log48 – 2 log43; 2) log6 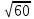 - log6 - log6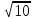 ; ; 3) 21 + log25 4) log83 + 3 log84 – 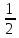 log89; log89; 5) log7 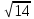 - log7 - log7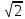 ; ; 6) 5 log510 - 1 7) 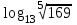 ; ; 8) 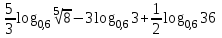 . .9) 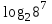 ; ; 10) 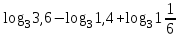 . .11) 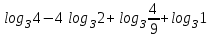 12) 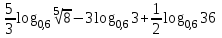 . .13) 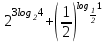 2 вариант 1. Найдите х: 1) log4 x = -2; 2) log64 x = 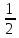 ; 3) log4 x = 3; ; 3) log4 x = 3; 4) log16 2 = x; 5) log3 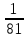 = x; 6) log4 64 = x; = x; 6) log4 64 = x; 7) logx 49 = 2; 8) logx 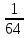 = -3; 9) logx 3 = = -3; 9) logx 3 = 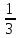 . . 10) log2 x = -4; 11) log81 x = 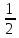 ; 12) log5 x = 3; ; 12) log5 x = 3; 13) log27 3 = x; 14) log2 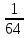 = x; 15) log6 216 = x; = x; 15) log6 216 = x; 16) logx 64 = 2; 17) logx 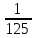 = -3; 18) logx 2 = = -3; 18) logx 2 = 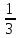 . . 2. Вычислите: 1) log69 + 2 log62 – lg1; 2) lg 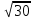 - lg - lg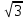 ; ; 3) 4 log48 - 1 4) lg 4 + 2 lg5 – lg1; 5) log5 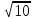 - log5 - log5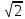 ; ; 6) 31 + log34 7) 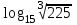 ; ; 8) 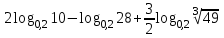 . .9) 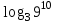 ; ; 10) 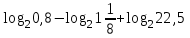 . .11) 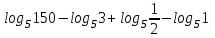 12) 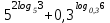 13) 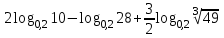 . .Практическая работа Показательные неравенства. ЦЕЛЬ: формирование навыков решения показательных неравенств. Уровень А Ответить на вопросы: Дайте определение показательной функции. Дайте определение показательного неравенства. Какие неравенства называются простейшими показательными неравенствами? Какие условия должны выполняться при решении показательных неравенств? Уровень Б Образцы решения неравенств:
Решить неравенства по образцу:
Практическая работа |

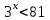
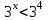
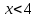
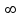 ; 4).
; 4).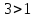 ,
, 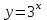 возр.
возр.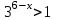
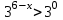
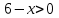
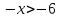
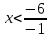
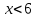
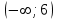 .
.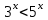
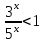
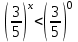
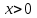
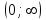
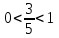 ,
,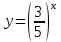 убыв.
убыв.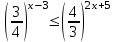
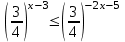
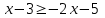
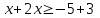
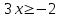
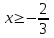
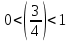 ,
, 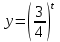 убыв. Ответ:
убыв. Ответ: 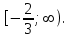
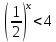
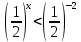
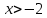
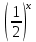 убыв.
убыв.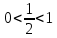
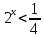
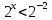
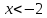
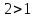
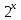 возр.
возр.