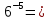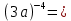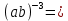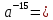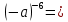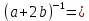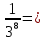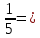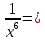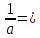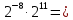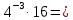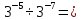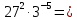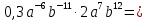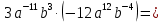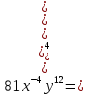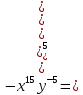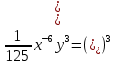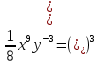Практическая работа. Математика. Практическая работа Приближённое значение. Абсолютная и относительная погрешности
 Скачать 0.85 Mb. Скачать 0.85 Mb.
|
|
Тема 1. Развитие понятия о числе Практическая работа Приближённое значение. Абсолютная и относительная погрешности. ЦЕЛЬ: научиться выполнять действия с приближёнными числами. ХОД РАБОТЫ 1. Изучите теорию и разобранные примеры по данной теме. 2. Выполните предложенные задания. Приближённое число есть такое число, которое отличается от точного на погрешность (ошибку), допущенную в соответствии с условиями данной задачи, и заменяет точное число в расчётной формуле. Арифметические действия с приближёнными числами следует производить также приближённо, ограничиваясь той степенью точности, которая необходима для данной задачи. 1.1 АБСОЛЮТНАЯ ПОГРЕШНОСТЬ Точные значения искомых величин будем обозначать буквами а0 , b0 , с0 … и т.д. На практике часто получают не точные, а приближённые значения величин, которые будем обозначать а1 , а2 , а3, … и т.д. (индексы – номер измерения). Если а0 – точное число, а – его приближённое значение, то а а0 . Абсолютная величина разности между точным и приближённым значением числа, т.е. ∆ = |а – а0|, называется истинной абсолютной погрешностью этого числа. 1. Найти истинную абсолютную погрешность числа а0 = 245,2, если а = 246. Р е ш е н и е. Имеем |а – а0| = |245,2 - 246| = 0,8. 2 – 9. Найти истинные абсолютные погрешности чисел: 2. а0 = 348; а = 347,289. 3. а0 = 64,28; а = 64,32. 4. а0 = 14,262; а = 14,261983. 5. а0 = 0,135; а = 0,13512. 6. а0 = 12487856; а = 12400000. 7. а0 = 3,528; а = 3,5281. 8. а0 = 854000; а = 853997. 9. а0 = 647398; а = 647500. Число Δа будем называть границей абсолютной погрешности. Если задана граница абсолютной погрешности Δа, то говорят, что число а есть приближённое значение числа а0 с точностью до Δа, и пишут а0 = а ± Δа . 10. Записать число а0 = 9,3 ± 0,5 с помощью двойного неравенства. Р е ш е н и е. 9,3 – 0,5 ≤ а0 ≤ 9,3 + 0,5; 8,8 ≤ а0 ≤ 9,8. 11 – 18. Записать числа в виде двойного неравенства: 11. а0 = 347,50; Δа = 0,0047. 12. а0 = 0,3010; Δа = 0,00005. 13. а0 = 7,269; Δа = 0,0004. 14. а0 = 142170; Δа = 30. 15. а0 = 420000; Δа = 500. 16. а0 = 7,263; Δа = 0,00001. 17. а0 = 0,1628; Δа = 0,0002. 18. а0 = 99,973; Δа = 0,027. В математике имеется ряд практических методов для оценки точности вычислений, в том числе и обязательные правила составления таблиц и проведения измерений. Так, абсолютная погрешность числа, взятого из математической таблицы, не превосходит единицы последнего разряда; при физических измерениях не очень большой точности измерения определяется по наименьшему делению прибора. 1.2. ЗАПИСЬ ПРИБЛИЖЁННЫХ ЧИСЕЛ Определение. Некоторая цифра приближённого числа считается верной, если его абсолютная погрешность Δа не превосходит единицы того разряда, в котором стоит эта цифра. В противном случае цифра называется сомнительной. Очевидно, что если какая-либо цифра верна, то и все предшествующие ей цифры также являются верными. 19. Найти верные и сомнительные цифры числа а0 = 945,673 ± 0,03. Р е ш е н и е. Здесь а = 945,673, Δа = 0,03. Цифра 6 представляет собой цифру десятых долей, т.е. единицу этого разряда запишем так: 0,1. Сравним эту единицу с погрешностью числа; так как 0,1 > 0,03, то абсолютная погрешность числа не превосходит единицы разряда, в котором стоит цифра 6. Следовательно, по определению, цифра 6 – верная. Очевидно, что цифры 9, 4, 5, стоящие перед цифрой 6, также являются верными. Цифра 7 – это цифра сотых долей, т.е. единицу этого разряда можно записать так: 0,01. Сравним эту единицу с погрешностью числа; поскольку 0,01 < 0,03, абсолютная погрешность числа больше единицы разряда, в котором стоит цифра 7. Следовательно, по определению, цифра 7 – сомнительная. Очевидно, что цифра 3 также является сомнительной. 20 – 31. Определить верные и сомнительные цифры чисел: 20. а0 = 649 ± 0,04. 21. а0 = 14,28 ± 0,03. 22. а0 = 1,298 ± 0,003. 23. а0 = 428,735 ± 6. 24. а0 = 24,68 ± 0,05. 25. а0 = 749,3 ± 5. 26. а0 = 1428 ± 0,05. 27. а0 = 729,5 ± 1. 28. а0 = 4,289 ± 0,2. 29. а0 = 679,3 ± 0,06. 30. а0 = 428,7 ± 20. 31. а0 = 64,28 ± 5. В записи приближённых чисел принято соблюдать следующие правила: Оставлять в записи приближённого числа только верные цифры. Если в десятичной дроби последние верные цифры нули, то их надо выписать. Если число содержит в конце нули, не являющиеся верными цифрами, то они должны быть заменены на 10n, где n – число нулей, которое надо заменить. 32. Записать правильно число: а) а = 0,075 ± 0,000005; б) а = 746000000 ± 5000. Р е ш е н и е. а) Так как погрешность числа не превосходит 0,00001, то число должно быть записано в виде а = 0,07500. б) Здесь первой верной цифрой является цифра десятков тысяч, поскольку погрешность числа не превосходит 10000. Значит, число должно быть записано в виде а = 74600 · 104 . 33 – 40. Записать правильно следующие приближённые числа: 33. а0 = 0,35; Δа = 0,00005. 34. а0 = 163000000; Δа = 500. 35. а0 = 765000; Δа = 5. 36. а0 = 0,3700; Δа = 0,05. 37. а0 = 278000; Δа = 50. 38. а0 = 428; Δа = 5. 39. а0 = 649,3; Δа = 5. 40. а0 = 172420; Δа = 0,05. 41. Указать абсолютную погрешность приближённого числа: а) а = 2175000; б) а = 173 · 104 . Р е ш е н и е. а) Так как выписаны все нули, то нули разряда сотен, десятков, единиц – верные цифры. Следовательно, абсолютная погрешность числа не превосходит единицы наименьшего разряда, в котором стоят верные цифры, т.е. Δа = 1. б) Согласно правилу III на 104 заменены нули, не являющиеся верными цифрами. Следовательно, первой верной цифрой является цифра 3 в разряде десятков тысяч. Итак, Δа = 10000. 42 – 52. Указать абсолютные погрешности следующих приближённых чисел: 42. а = 14,5 · 10. 43. а = 263 · 104 . 44. а = 748,56. 45. а = 34,20. 46. а = 759,00. 47. а = 64,27. 48. а = 23,560. 49. а = 1,0000. 50. а = 147,3 · 103 . 51. а = 142,3 · 10. 52. а = 596,2 · 105 . 53. а = 15,7 · 102 . 54 – 71. Записать правильно следующие приближённые числа, учитывая, что Δа = 500 54. а = 15400. 55. а = 24300. 56. а = 2600. 57. а = 4000. 58. а = 600. 59. а = 56100. 60. а = 1700. 61. а = 41500. 62. а = 89300. 63. а = 666400. 64. а = 759200. 65. а = 111600. 66. а = 35200. 67. а = 74900. 68. а = 54300. 69. а = 7500. 70. а = 1628300. 71. а = 428600. Значащими цифрами числа называют все его верные цифры, за исключением нулей, стоящих левее первой цифры, отличной от нуля. Например, число 0,712 содержит три значащие цифры: 7, 1, 2; число 0,0016 – две значащие цифры: 1, 6; число 45,03 – четыре значащие цифры: 4, 5, 0, 3. 1.3. ОКРУГЛЕНИЕ ПРИБЛИЖЁННЫХ ЧИСЕЛ Запись приближённых чисел требует их округления. Чтобы округлить число с точностью до указанного разряда, нужно цифры, стоящие правее указанного разряда, отбросить (в дробной части числа) или заменить нулями (в целой части числа). Если при округлении первая отбрасываемая цифра меньше 5, то последнюю сохраняемую цифру не изменяют; если первая отбрасываемая цифра больше или равна 5, то последнюю сохраняемую цифру увеличивают на 1. 72. Округлить с точностью до 0,01: а) 1,423; б) 3,2387; в) 1,996. Р е ш е н и е. а) Так как отбрасываемая цифра 3 < 5, то округляем до 1,42; б) так как первая отбрасываемая цифра 8 > 5, то округляем до 3,24 ; в) так как первая отбрасываемая цифра 6 > 5, то округляем до 2,00. 73 – 83. Округлить с точностью до 0,01 следующие числа: 73. 0,428. 74. 2,645. 75. 8,993. 76. 16,452. 77. 25,689. 78. 81,341. 79. 10,328. 80. 76,645. 81. 62,8428. 82. 15,1613. 83. 17,8975. 84. 22,1488. 85 – 93. Округлите с точностью до 1 следующие числа: 85. 16,285. 86. 17,349. 87. 34,931. 88. 60,605. 89. 0,785. 90. 2,501. 91. 31,499. 92. 785,501. 93. 0,499. 94 – 102. Округлите с точностью до 1000 следующие числа: 94. 1835. 95. 4382. 96. 64975. 97. 10428. 98. 72356. 99. 16765. 100. 4172,035. 101. 6872,73. 102. 1335,42. 1.4. ОТНОСИТЕЛЬНАЯ ПОГРЕШНОСТЬ Допустим, что погрешность какого-либо измерения равна 0,2 см. Если с такой погрешностью измеряли длину тетради, то это большая погрешность, а если измеряли длину комнаты – небольшая. Таким образом, имеет значение не только какова погрешность, но и отношение её к измеряемой величине. Относительной погрешностью приближённого значения числа а называется отношение абсолютной погрешности этого числа к числу а. Так как абсолютная погрешность обычно бывает неизвестна, то на практике используют понятие границы относительной погрешности числа. Границей относительной погрешности ɛα приближённого значения а называется отношение границы абсолютной погрешности Δа к модулю числа а, т.е. ɛα = 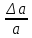 . .Чем меньше граница относительной погрешности, тем выше качество измерения. 103. Найти границу относительной погрешности числа а = 142,5, если Δа = 0,05. Р е ш е н и е. ɛα = 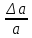 ∙ 100% , ɛα = ∙ 100% , ɛα = 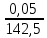 ∙ 100% = 0,00034 ∙ 100% = 0,03% . ∙ 100% = 0,00034 ∙ 100% = 0,03% .104 – 111. Определить границы относительных погрешностей следующих чисел: 104. а= 6,93; Δа = 0,02.105. а= 12,79; Δа = 2 . 106. а= 648,5; Δа = 0,05. 107. а= 792,3; Δа = 0,05. 108. а= 2,372; Δа = 0,004. 109. а= 4,25; Δа = 0,02. 110. а= 34,27; Δа = 0,005. 111. а= 1,9345; Δа = 0,0005. 112. Найти границу абсолютной погрешности числа а = 1348, если ɛα = 0,04% . Р е ш е н и е. Запишем границу относительной погрешности в виде 0,04% = 0,0004. Чтобы найти границу абсолютной погрешности числа а, воспользуемся формулой Δа = | а | ∙ ɛα ,откуда Δа = 1348 ∙ 0,0004 = 0,539 ≈ 0,5. Значит, Δа = 0,05 и число может быть записано так: а = 1348 ± 0,5. 113 – 118. Найти границу абсолютной погрешности следующих чисел: 113. а = 352,004; ɛα = 0,03% . 114. а = 71,28; ɛα = 0,005% . 115. а = 0,649; ɛα = 0,002% . 116. а = 42,78; ɛα = 3% . 117. а = 142,5; ɛα = 0,3% . 118. а = 740000,0; ɛα = 0,05% . Практическая работа Проценты Решение задач на проценты и концентрацию. ЦЕЛИ И ЗАДАЧИ: Помочь обучающимся осознать практическую значимость данного материала. Создать условия для развития у студентов умений анализировать текст задачи, формулировать проблему, предлагать пути её решения. Организовать деятельность учащихся по изучению и первичному закреплению понятиям смесь, концентрация. Продолжить формирование навыка нахождения процентного отношения. Задание. Произвести расчеты ( ответы записать на листах, с последующей проверкой) Найти 25 % от 56 Сколько % составит 30 от 75? Найдите число, 20% которого равны 12. Какое число, увеличенное на 13% составит 339 ? На сколько % число 150 больше числа 120? В магазине А цену на товар сначала увеличили на 30%, затем снизили на 30%. В магазине Б - снизили на 30 %, затем увеличили на 30%. Где выгодно совершить покупку? Задача 1. При оплате услуг через платежный терминал взымается комиссия 5%. Терминал принимает суммы кратные 10 рублям. Аня хочет положить на счет своего мобильного телефона не меньше 300 рублей. Какую минимальную сумму она должна положить в приемное устройство данного терминала? Задача 2. На покупку планшета взяли кредит 20000 р на 1 год под 16 % годовых . Вычислите, сколько денег необходимо вернуть банку, какова ежемесячная сумма выплат? Задача 3. Мобильный телефон стоил 5000 рублей. Через некоторое время цену на эту модель снизили до 3000 рублей. На сколько процентов была снижена цена? Задача 4. Смешали 8 литров 15-процентного водного раствора некоторого вещества с 12 литрами 25-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора? Решение:
Задача 5. Один раствор содержит 20 % соли, а второй – 70 %. Сколько граммов первого и второго раствора нужно взять, чтобы получить 100 г 50% раствора. Задача 6. Первый сплав содержит 10 % меди, второй - 25 % меди. Из этих двух сплавов получили третий сплав массой 30 кг, содержащий 20 % меди. Какое количество каждого сплава было использовано? Тема 2. Корни, степени и логарифмы Практическая работа Степень с натуральным и целым показателем и её свойства. ЦЕЛЬ: выполнить действия по преобразованию выражений, содержащих натуральные и целые степени. СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ 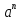 = =Свойства: При умножении степеней с одинаковыми основаниями показатели складываются, а основание остается неизменным. 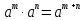 При делении степеней с одинаковыми основаниями показатели вычитаются, а основание остается неизменным. 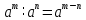 При возведении степени в степень показатели перемножаются. 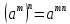 При возведении в степень произведения двух чисел, каждое число возводят в эту степень, а результаты перемножают. 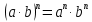 Если в степень возводят частное двух чисел, то в эту степень возводят числитель и знаменатель, а результат делят друг на друга. 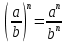 Если 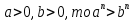 СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ 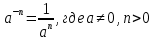 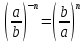 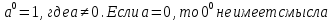 По определению: 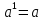  Свойства: 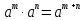 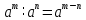 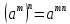 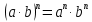 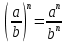 Пусть r рациональное число 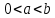 , тогда , тогда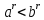 при r>0 при r>0 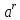 > >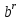 при r<0 при r<07 .Для любого рациональных чисел r и s из неравенства 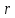 > >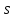 следует следует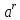 > >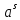 при a>1 при a>1 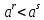 при при  Формулы сокращённого умножения. 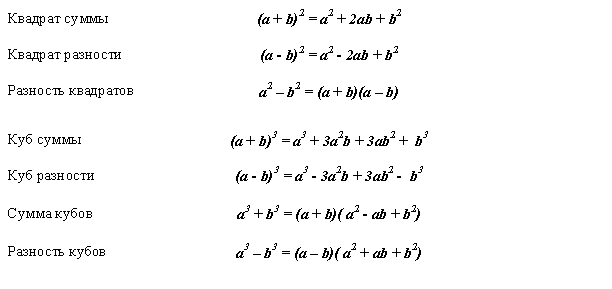 Выполнить самостоятельно Замените степень с целым отрицательным показателем дробью:
Замените дробь степенью с целым отрицательным показателем:
Вычислите:
Упростите выражение и найдите его значение при a=10, b=2:
Впишите пропущенное основание степени:
Практическая работа Степенная функция. Преобразование графиков степенной функции. Практическая работа Логарифмы и их свойства. Правила логарифмирования. Практическая работа Показательные неравенства. Практическая работа Логарифмические уравнения и неравенства. |