Практика. Практическая работа Способы обработки, хранения, поиска информации

• Название: Практическая работа Способы обработки, хранения, поиска информации
• Анкор: Практика
• Дата: 05.11.2022
• Размер: 0.53 Mb.
• Имя файла: OTIprakticheskieraboti22.docx
• Тип: Практическая работа; #771299
• страница: 2 из 6

Получаем 0,65625₁₀ = 0,52₈
Перевод вещественных чисел, т.е. чисел, содержащих целую и дробную части, осуществляется в два этапа. Отдельно переводится целая часть, отдельно — дробная. В итоговой записи полученного числа целая часть отделяется от дробной запятой.

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему счисления очень прост; достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) для восьмеричной системы счисления или тетрадой (четверкой цифр) для шестнадцатеричной системы счисления.
Примеры.
5 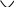37,1₈ = 101 011 111, 001₂
5 3 7 1

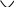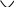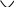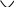1 A3,F₁₆ = 1 1010 0011, 1111₂
1 A 3 F
Чтобы перевести число из двоичной системы счисления в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады или тетрады и каждую такую группу заменить соответствующей восьмеричной или шестнадцатеричной цифрой.

Таблица соответствия систем счисления, используемых в ПК

Десятичная	Двоичная	Восьмеричная	Шестнадцатеричная
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F

Задания на практическую работу

Задание 1.

Перевести числа в систему счисления с основанием 10:

111,01₂; 30,02₄; 1101,101₂; 514₇; 341₆;

Задание 2. Перевести числа из одной системы счисления в другую

17₁₀→X₂

483₁₀ → X₂

483₁₀ → X₈

523₁₀ → X₈

812₁₀ → X₈

Содержание отчёта. Отчёт выполняется в тетради для практических занятий

1. 
   В отчете указывается цель работы
   
2. 
   Краткое изложение теории
   
3. 
   Задание и полное решение задания
   
4. 
   Вывод
   

Пример выполнения заданий
Задание 1. Перевести числа 111,01₂ и 30,02₄ в систему счисления с основанием 10: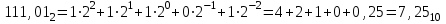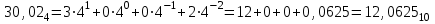



Задание 2. Перевести числа из одной системы счисления в другую: 17₁₀→X₂
1). Перевести 16₁₀ в двоичную систему счисления.

Число	Делитель	Целочисленный остаток
16 8 4 2 1	2 2 2 2	0 0 0 0 1

Получаем 16₁₀ = 10000₂
ПРАКТИЧЕСКАЯ РАБОТА 4 Применение правил недесятичной арифметики

Цель:

• 
  применять правила недесятичной арифметики;
  

Краткие сведения

Основные арифметические операции: сложение, вычитание, умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны - это сложение, вычитание, умножение столбиком и деление углом. Эти правила при­менимы и ко всем другим позиционным системам счисления. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы.

Сложение. Таблицы сложения легко составить, используя Правило Счета.



При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.

Умножение. Выполняя умножение многозначных чисел в различ­ных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимство­вать из соответствующих рассматриваемой системе таблиц умножения и сложения.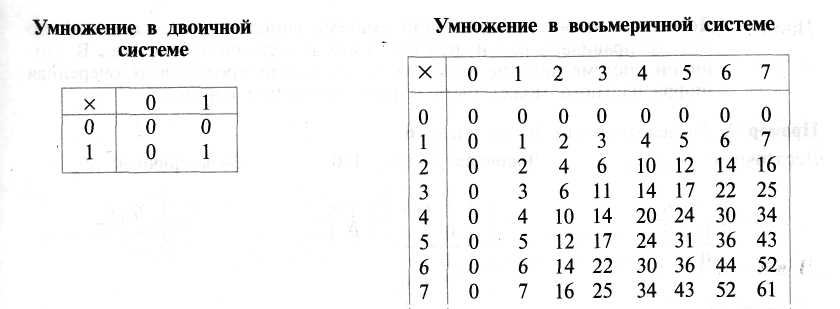



Ввиду простоты таблицы умножения в двоичной системе умножение сводится лишь к сдвигам множимого и сложениям.
Задания на практическую работу

1001₂+110₂

17₈+6₈

17₈+7₈+3₈

СD₁₆-AB₁₆

100₈-1₈

5₈*6₈
Содержание отчёта

5. 
   Отчёт выполняется в тетради для практических занятий
   
6. 
   В отчете указывается цель работы
   
7. 
   Краткое изложение теории
   
8. 
   Задание и полное решение задания
   
9. 
   Вывод
   

Примеры выполнения заданий

1001₂+110₂

	1	0	0	1	2
+		1	1	0	2
	1	1	1	1
				1+0=1
			0+1=1
		0+1=1

Проверка. Посчитаем данную сумму в десятичном виде.

1001₂=1*2³+0+0+1*2⁰=9₁₀

110₂=1*2²+1*2¹+0=6₁₀

1111₂=1*2³+1*2²+1*2¹+1*2⁰=15₁₀

9+6=15
СD₁₆-AB₁₆

		C	D	16
-		A	B	16
		2	2
			13-11=2
		12-10=2

Проверка.

CD₁₆=12*16¹+13*16⁰=205₁₀

AB₁₆=10*16¹+11*16⁰=171₁₀

22₁₆=2*16¹+2*16⁰=34₁₀

205-171=34
Пример. Сложим числа 15 и 6 в различных системах счисления.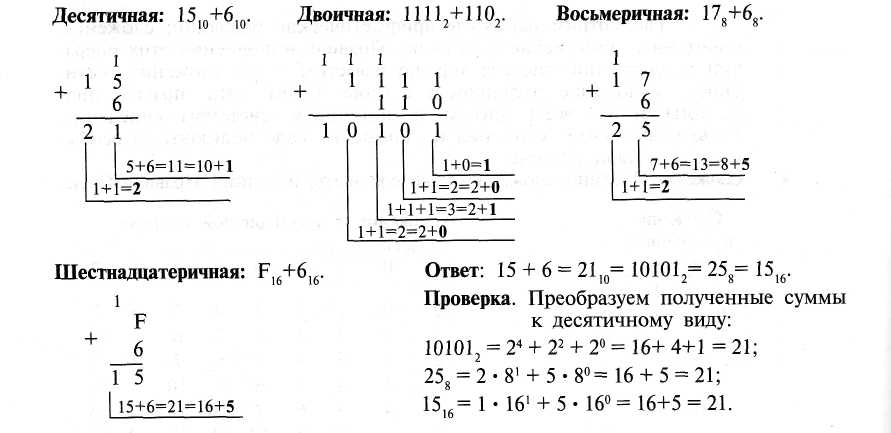



Пример Вычтем единицу из чисел 10₂, 10₈ и 10_]6.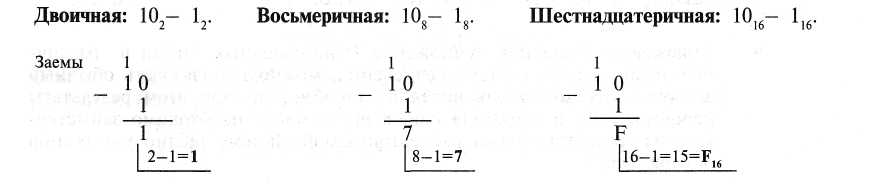



Пример. Вычтем число 59,75 из числа 201,25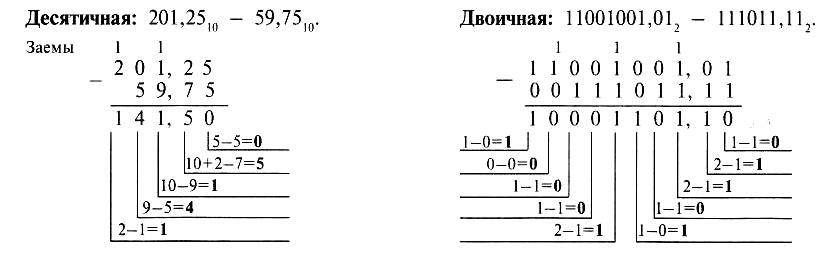



Пример. Перемножим числа 5 и 6.


Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В дво­ичной системе деление выполняется особенно просто: ведь очередная цифра частного может быть только нулем или единицей.

Пример. Разделим число 30 на число 6.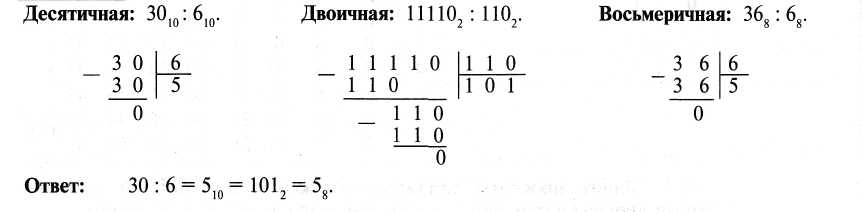

ПРАКТИЧЕСКАЯ РАБОТА 5. Вероятностный подход к расчету количества информации. Расчет вероятности события. Расчет условной и полной вероятности.

Цель: освоить методы теории вероятности с целью применения при определении количества информации

ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ

Событием в теории вероятностей называется всякий факт, который может произойти в результате некоторого испытания. Наблюдаемые нами события можно подразделить на следующие три вида: достоверные, невозможные, случайные. Событие достоверное, если при всех испытаниях рассматриваемое событие всегда наступает. Например, при взрыве снаряда достоверное событие – разрушение оболочки. Событие невозможное, если при всех испытаниях событие никогда не наступает. Например, при отсутствии тока в электрической цепи невозможное событие – загорание лампочки. Событие случайное, если в результате испытания событие может появиться или не появиться. Например, выигрываем на купленный билет лотереи.

Пространством элементарных исходов называется множество всех взаимно исключающихся исходов испытания. Его обозначают  . Те исходы, при которых интересующее нас событие наступает, назовем благоприятствующими этому событию. Вероятностью события А называется отношение числа m благоприятствующих этому событию исходов к общему числу n равновозможных несовместных элементарных исходов испытания и обозначается p(A) .

Свойства вероятностей: 1. Вероятность достоверного события равна единице. 2. Вероятность невозможного события равна нулю. 3. Вероятность случайного события заключена между нулем и единицей 0  p(A) 1.

Относительной частотой события называется отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний и обозначается w(A). Отличие классической вероятности события от его частоты состоит в том, что вероятность вычисляют до опыта, а относительную частоту – после опыта. Относительную частоту или число, близкое к ней, принимают в качестве статистической вероятности.

Перестановками называют комбинации, состоящие из одних и тех же различных элементов и отличающихся только порядком следования. Число всех возможных перестановок из n различных элементов равно P_n= n!.

Размещениями называют комбинации, составленные из n различных элементов по k , которые отличаются либо составом элементов, либо порядком следования. Число возможных размещений из n различных элементов по k равно A^k_n   (n )!/(n-k)!.

Сочетаниями называют комбинации, составленные из n различных элементов по k , которые отличаются составом элементов. Число возможных сочетаний из n различных элементов по k равно C^k_n   (n )!/k!(n-k)!

Пример. В партии из 10 деталей 7 стандартных. Найти вероятность, что среди 6 взятых наудачу деталей 4 стандартных. Решение. Общее число возможных элементарных исходов равно числу способов, которыми можно взять 6 деталей из 10, т.е. n  C⁶₁₀ . Подсчитаем исходы, благоприятствующие интересующему нас событию: 4 стандартных из 7 можно взять C⁴₇ способами, при этом остальные 2 детали должны быть нестандартными, их можно взять из 3 нестандартных деталей C²₃ способами. Искомая вероятность равна (C⁴₇ C²₃ )/ C⁶₁₀₌ (5 6 7 3 24)/(6 7 8 9 10)  0,5 .

ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ ВЕРОЯТНОСТЕЙ

Суммой А+В двух событий А и В называют событие, состоящее в появлении хотя бы одного из них. Суммой нескольких событий А1 + А2 +...+ Аn называют событие, которое состоит в появлении хотя бы одного из этих событий.

Теорема сложения вероятностей несовместимых событий: Вероятность появления одного из двух несовместимых событий, равна сумме вероятностей этих событий: p(A B)  p(A)  p(B).

Следствие: Вероятность появления одного из нескольких несовместных событий равна сумме вероятностей этих событий.

Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий. Условной вероятностью Р_А(В) называют вероятность события B, вычисленную в предположении, что событие А уже наступило.

Теорема умножения вероятностей: Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже произошло p(AB)= p(A) p_A (B) .

Следствие: Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже произошли

Событие называется противоположным событию A , если оно наступает тогда, когда A не наступает. Для противоположных событий справедливо утверждение о том, что сумма вероятностей противоположных событий равна 1.

Два события называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании.

Теорема сложения вероятностей совместных событий: Вероятность появления хотя бы одного из двух совместных событий равна p(A B)  p(A)  p(B)  p(AB). Пример. В урне 5 белых и 6 черных шаров. Из урны извлекаются шары до появления черного шара. Найти вероятность, что произведено ровно три извлечения, если: а) после каждого извлечения шар возвращается в урну; б) извлеченные шары откладываются в сторону. Решение. Обозначим через Ai событие, состоящее в появлении черного шара при i -ом извлечении.

а) эти события независимы, поэтому вероятность равна произведению вероятностей 2-х противоположных событий и самого события p(A)=(5/11 5/11 6/11)

б) эти события зависимы, поэтому вероятность равна произведенмю вероятности противоположного события на относительную вероятность наступления одного противоположного события при наступления противоположного события и на относительную вероятность самого события при условии наступления двух противоположных событий , т.е. p=(5/11 4/10 6/9) = 4/33

ФОРМУЛА ПОЛНОЙ ВЕРОЯТНОСТИ

Пусть событие A может наступить при условии появления одного из несовместных событий B₁ B_2… B_n, образующих полную группу (т.е. сумма этих событий есть достоверное событие и никакие два из них не могут произойти одновременно). Пусть известны вероятности этих событий и условные вероятности

Формула полной вероятности: Вероятность события А, которое может наступить при условии появления одного из несовместных событий B₁ B_2… B_n, образующих полную группу равна: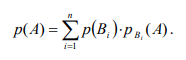



ГЕОМЕТРИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ

Пусть плоская фигура g составляет часть плоской фигуры G . На фигуру G наудачу бросается точка. Это означает, что все точки области G «равноправны» в отношении попадания туда брошенной случайной точки. Полагая, что вероятность события A – попадания брошенной точки на фигуру g – пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно G , ни от формы g , найдем p(A)  S_g/ S_G , где S_g и S_G  соответственно площади областей g и G . Область, на которую распространяется понятие геометрической вероятности, может быть одномерной (прямая, отрезок) и трехмерной (некоторое тело в пространстве). Обозначая меру (длину, площадь, объем) области через mes , приходим к следующему определению. Геометрической вероятностью события называется отношение меры области, благоприятствующей появлению события A , к мере всей области, т.е. p(A)  mes g/ mes G.