Практика. Практическая работа Способы обработки, хранения, поиска информации

• Название: Практическая работа Способы обработки, хранения, поиска информации
• Анкор: Практика
• Дата: 05.11.2022
• Размер: 0.53 Mb.
• Имя файла: OTIprakticheskieraboti22.docx
• Тип: Практическая работа; #771299
• страница: 3 из 6

Задание

1. Бросают игральный кубик. Какова вероятности выпадания четного количества очков?

2.В корзине 4 груши, 9 яблока и 3 апельсина. Рассчитать вероятность того, что возьмут грушу

2. В коробке имеется 30 белых, 15 черных и 5 красных мячей. Определите вероятности выпадения мячей разных цветов

3.Бросают два игральных кубика. Какова вероятность того, что выпадет 7 очков?

4. В урне 3 белых и 2 черных мяча. Какова вероятность того, что первым возьмут белый шар, а вторым черный?

5. Какова вероятность того, что 2карты, вынутые из колоды в 36 карты, окажутся одной масти
Содержание отчета

Название и цель работы.

Краткое изложение теории/методики

Задание и ход его выполнения

Выводы
ПРАКТИЧЕСКАЯ РАБОТА 6 Расчет количество информации. Использование формулы Хартли и формулы Шеннона  при решении задач на определение количества информации

Цель работы

Уметь измерять количество информации;

Краткие теоретические сведения

Р. Хартли предложил формулу по оценке сообщений:
I = log₂ K ,


где К - количество равновероятных событий; I - количество бит в сообщении, такое, что любое из К событий произошло. Тогда K=2^I.
Формулу Хартли можно записать так:

I = log₂ K = log₂ (1 / р) = - log₂ р,

где р – вероятность события
т. к. каждое из К событий имеет равновероятный исход р = 1 / К, то К = 1 / р.
Если события имеют разные вероятности р1,p2,…,pm, с которыми система принимает одно из своих состояний (a1,a2,…am), где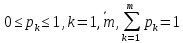
применяется формула Шеннона:


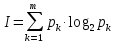Задания на практическую работу

1.В корзине 4 груши, 9 яблока и 3 апельсина. Определить количество информации в зрительном сообщении: «Человек взял грушу».

2. В коробке имеется 30 белых, 15 черных и 5 красных мячей.

1. 
   Определите вероятности выпадения мячей разных цветов
   
2. 
   Определите количество информации в сообщении «Достали белый мяч»;
   
3. 
   Определите количество информации в сообщении «Достали черный мяч»;
   
4. 
   Определите количество информации в сообщении «Достали красный мяч».
   

3.Шарик находится в одной из трех урн: А, В или С. Определить сколько бит информации содержит сообщение о том, что он находится в урне В.

 4.При угадывании целого числа в диапазоне от 1 до N было получено 5 бит информации. Чему равно N?
Содержание отчёта

Отчёт выполняется в тетради для практических занятий

В отчете указывается цель работы

Краткое изложение теории

Задание и полное решение задания

Вывод
Методические указания

Пример1

   Шарик находится в одной из трех урн: А, В или С. Определить сколько бит информации содержит сообщение о том, что он находится в урне В.

   Решение.

   Такое сообщение содержит I = log₂ 3 = 1,585 бита информации.   

Пример 2

   При угадывании целого числа в диапазоне от 1 до N было получено 7 бит информации. Чему равно N?

   Решение.

   I = log₂ K; K= 2^I = 2^7 =128 (чисел)
Пример 3 выполнения заданий

В корзине 4 груши, 3 яблока и 2 апельсина. Определить количество информации в зрительном сообщении: «Оля взяла грушу».

Решение: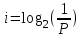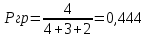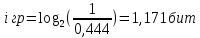





Ответ: 1,171 бит
Практическая работа 7. Применение теоремы Котельникова.

Цель: научиться применять теорему Котельникова

Краткие теоретические сведения.

Теорема отсчетов. Математическая модель системы передачи информации.

Теорему Котельникова можно объяснить следующим образом. Если надо передать некий сигнал, то не обязательно передавать его целиком. Можно передавать его мгновенные импульсы. Частота передачи этих импульсов называется частотой дискретизации в теореме Котельникова.. Для разного типа сигналов существуют разные частоты дискретизации. Для речевого (телефонного) сообщения при ширине канала 3,4 кГц - 6,8 кГц, а для телевизионного сигнала - 16 мГц.

Согласно теореме Котельникова любой непрерывный сигнал  с конечным спектром (имеющим максимальное значение  ) можно представить в виде дискретных отсчетов  , частота дискретизации которых должна быть выбрана не менее чем в два раза выше максимального значения спектра сигнала: , передать его по линии связи, а затем восстановить исходный аналоговый сигнал.

Теорема Котельникова утверждает, что если требуется передать непрерывный сигнал  с ограниченным спектром по каналу связи, то можно не передавать все его значения: достаточно лишь передать его мгновенные значения (отсчеты) через интервал  . Поскольку сигнал  полностью определяется этими значениями, то по ним он может быть восстановлен на приемном конце системы связи. Для этого достаточно соединить отсчеты плавной кривой. Это можно объяснить тем, что сигнал  между отсчетами может изменяться только плавно, так как частоты выше  дающие быстрые изменения, в сигнале отсутствуют. Ведь отсчеты берутся достаточно часто, и тем чаще, чем выше максимальная частота  .

Частота следования импульсов, называемая также частотой дискритизации, определяется по теореме Котельникова:

.

Например, частота дискретизации для речевого (телефонного) сигнала, имеющего максимальное значение спектра сигнала  , будет равна 

Теорема Найквиста—Шеннона—Котельникова

Теорема гласит (упрощенно), что для сигнала, представленного последовательностью дискретных отсчетов, точное восстановление возможно, только если частота дискретизации более чем в 2 раза выше максимальной частоты в спектре сигнала.

Из сказанного следует, что восстановить без искажений можно только сигнал, спектр которого ограничен некоторой частотой F_max (частота Найквиста).

Однако, теоретически все реальные сигналы имеют бесконечные спектры. Спектры реальных сигналов, хотя и не бесконечны, но могут быть очень широкими. Для того чтобы при дискретизации избежать искажений, вызванных этим обстоятельством, сигнал вначале пропускают через фильтр, подавляющий в нем частоты, превышающие заданное значение F_max, и лишь затем производят дискретизацию: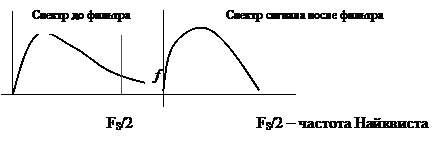



Итак, согласно теореме, рассматривающей идеальные условия, частота дискретизации, с которой следует брать отсчеты, составляет не менее 2F_max. 

Рассмотрим пример. Выбрать частоту дискретизации и определить переходную полосу частот для ФНЧ при дискретизации сигналов вещания первого класса с диапа­зоном частот 0,05 ... 10 кГц.

Решается на основании теоремы Котельникова. Следовательно, в нашем слу­чае F_д>20 кГц. Для телефонного сигнала стандартная частота дискретизации F_д = 8 кГц. При организации канала вещания (вместо трех телефонных кана­лов) частота дискретизации сигналов вещания должна быть кратна частоте дискретизации телефонного канала и равна 8·3=24 кГц.

Рассмотрим другой пример. Определить продолжительность импульса в групповом цифровом сигнале 24-х канальной ЦСП. Частота дискретизации F_д=8 кГц. Скважность импульсов Q=2. Разрядность кода m=8.

Решение:   , кГц

 , мкс

 , мкс

 Задание

Определить продолжительность импульса в групповом цифровом сигнале 24-х каналов. Частота дискретизации F_д=16 кГц. Скважность импульсов Q=2. Разрядность кода 16=8.

Содержание отчета

Название и цель.

Кратко теория

Задание и ход выполнения

Выводы
ПРАКТИЧЕСКАЯ РАБОТА 8. Применение законов аддитивности информации

Цель: изучить закон аддитивности информации и научиться его применять.

Краткие теоретические сведения

Аддитивность — свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям, в некотором классе возможных разбиений объекта на части. Например, аддитивность объёма означает, что объём целого тела равен сумме объёмов составляющих его частей.

Закон аддитивности информации

Количество информации H(x1, x2), необходимое для установления пары (x1, x2), равно сумме количеств информации H(x1) и H(x2), необходимых для независимого установления элементов x1 , x2: H(x1, x2) = H(x1) + H(x2).

Задание.

№1

В течение 5 секунд было передано сообщение, объем которого составил 750 байт. Каков размер алфавита, с помощью которого записано сообщение, если скорость передачи составила 200 символов в секунду?

№2

Какое количество информации несет достоверный прогноз погоды в предположении, что прогноз погоды на следующий день заключается в предсказании дневной температуры (обычно выбор делается из 16 возможных для данного сезона значений) и одного из четырех значений облачности (солнечно, переменная облачность, пасмурно, дождь).
Содержание отчета

Название и цель.

Кратко теория

Задание и ход выполнения

Выводы
ПРАКТИЧЕСКАЯ РАБОТА 9. Кодирование звуковой информации

Цель работы: Ознакомиться с принципами кодирования звуковой информации. Научиться рассчитывать информационный объем звукового файла

Теоретические сведения

Кодирование звуковой информации - звуковая информация может быть представлена последовательностью элементарных звуков (фонем) и пауз между ними.

Компьютер работает с цифровой информацией, которую можно представить в виде серии электрических импульсов - логических нулей и единиц.

Каждый звук кодируется и хранится в памяти. Вывод звуков из компьютера осуществляется синтезатором речи, который считывает из памяти хранящийся код звука.

Временная дискретизация звука. Звук представляет собой звуковую волну с непрерывно меняющейся амплитудой и частотой. Чем больше амплитуда сигнала, тем он громче для человека, чем больше частота сигнала, тем выше тон. Для того чтобы компьютер мог обрабатывать звук, непрерывный звуковой сигнал должен быть превращен в последовательность электрических импульсов (двоичных нулей и единиц). В процессе кодирования непрерывного звукового сигнала производится его временная дискретизация. Непрерывная звуковая волна разбивается на отдельные маленькие временные участки причем для каждого такого участка устанавливается определенная величина амплитуды. Непрерывная зависимость амплитуды сигнала от времени A(t) заменяется на дискретную последовательность уровней громкости. На графике это выглядит как замена гладкой кривой на последовательность «ступенек». Глубина кодирования. Каждой «ступеньке» присваивается определенное значение уровня громкости звука. Уровни громкости звука можно рассматривать как набор возможных состояний N, для кодирования которых необходимо определенное количество информации I, которое называется глубиной кодирования звука. Временная дискретизация звука.

Глубина кодирования звука — это количество информации, которое необходимо для кодирования дискретных уровней громкости цифрового звука.

Частота дискретизации.

Качество цифрового звука зависит от количества измерений уровня громкости звука в единицу времени, т. е. частоты дискретизации. Чем большее количество измерений производится за 1 секунду (чем больше частота дискретизации), тем точнее «лесенка» цифрового звукового сигнала повторяет кривую аналогового сигнала. Частота дискретизации звука — это количество измерений громкости звука за одну секунду.

Качество оцифрованного звука.

Чем больше глубина и частота дискретизации звука, тем более качественным будет звучание оцифрованного звука.

Информационный объем звукового файла Следует отметить, что чем выше качество цифрового звука, тем больше информационный объем звукового файла. Оценим информационный объём моноаудиофайла (V), это можно сделать, используя формулу: V=t⋅√ ⋅I, где t — общая длительность звучания, выражаемая в секундах, √ — частота дискретизации (Гц), I— глубина кодирования (бит).

При стереозвучании следует еще умножить на 2 (две звуковые дорожки): V=2t⋅√ ⋅I

Основные методы кодирования звуковой информации Существуют различные методы кодирования звуковой информации двоичным кодом, среди которых выделяют два основных направления: метод FM и метод Wave-Table. Метод FM (Frequency Modulation)-фрагментационной модуляции основан на том, что теоретически любой сложный звук можно разложить на последовательность простейших гармонических сигналов разных частот, каждый из которых будет представлять собой правильную синусоиду, а это значит, что его можно описать кодом. Процесс разложения звуковых сигналов в гармонические ряды и их представление в виде дискретных цифровых сигналов происходит в специальных устройствах, которые называют «аналогово-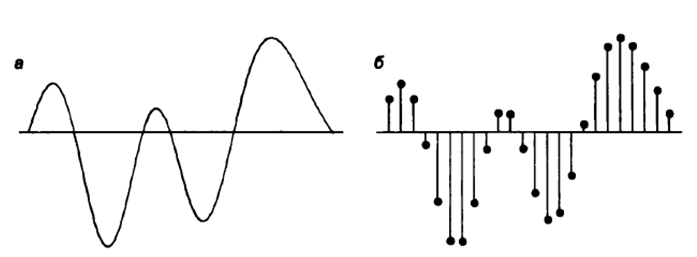

цифровые преобразователи» (АЦП).

На рисунке изображен звуковой сигнал на входе АЦП, а на рисунке 2б изображен уже преобразованный дискретный сигнал на выходе АЦП.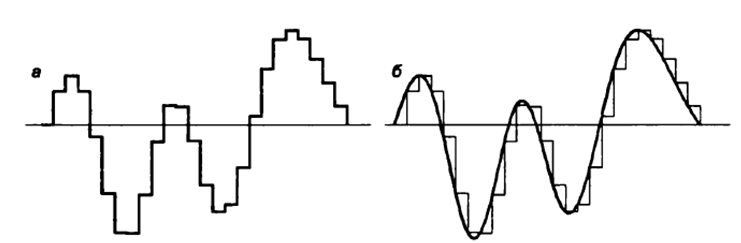


Для обратного преобразования при воспроизведении звука, который представлен в виде числового кода, используют цифро-аналоговые преобразователи (ЦАП).

Таблично-волновой метод (Wave-Table) основан на том, что в заранее подготовленных таблицах хранятся образцы звуков окружающего мира, музыкальных инструментов и т. д. Числовые коды выражают высоту тона, продолжительность и интенсивность звука и прочие параметры, характеризующие особенности звука. Поскольку в качестве образцов используются «реальные» звуки, качество звука, полученного в результате синтеза, получается очень высоким и приближается к качеству звучания реальных музыкальных инструментов.
Задание.

№1.

Рассчитать в битах объем звукового файла, длительность звучания в течении 90 секунд при качестве звука, при котором частота дискретизации 24 кГц, а глубина кодирования 16 бит, перевести в байты, килобайты и Мбайты.

№2 Оценить информационный объём цифрового звукового файла, у которого длительность звучания равна 5 секундам при качестве звука при качестве звука, при котором частота дискретизации 24 кГц, а глубина кодирования 16 бит, расчет произвести в битах. Перевести в байты и килобайты.

№3 Оценить информационный объём цифрового стереозвукового файла, у которого длительность звучания равна 3 секундам при качестве звука, при котором частота дискретизации 24 кГц, а глубина кодирования 16 бит, расчет произвести в битах. Перевести в байты и килобайты.

№4. Рассчитать длительность звучания стереозвукового файла, информационный объем которого 384000 байта при качестве звука :16 битов, 48 000 измерений в секунду.
Содержание отчёта.

В отчете указывается цель работы

Краткое изложение теории

Задание и полное решение задания

Вывод
Приложение.

Примеры расчета.

1) если длительность звучания равна 1 минуте и имеем качество звука, при котором частота дискретизации 24 кГц, а глубина кодирования 16 бит, то:

V=60*24000*16(бит)=23040000бит=2880000байт=2812,5кбайт=2,75Мбайт

1 Бит - минимальная единица информации.

Для справки:

8 Бит = 1 Байт

1024 Байта = 1 Килобайт

1024 Килобайта = 1 Мегабайт

1024 Мегабайта = 1 Гигабайт

2) оценим информационный объём цифрового стереозвукового файла, у котрого длительность звучания равна 1 секунде при качестве звука (16 битов, 24000 измерений в секунду). Для этого глубину кодирования умножим на количество измерений в 1 секунду и умножить на 2 (стереозвук):

стерео-умножаем на два.

V=16*24000*2(бит)=768000бит=96000байт=93,75кбайт