Математика. ПРАКТИЧЕСКИЕ ЗАНЯТИЯ. Практические занятия
 Скачать 291.73 Kb. Скачать 291.73 Kb.
|
|
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ 1. (задачи 7.01-710 КР №7) В коробке 5 синих и 3 красных карандаша. Вынимаем случайным образом один карандаш. Какова вероятность того, что он: а) синий; б) красный; в) зеленый; г) синий или красный? Решение. Число возможных исходов n=5+3=8 а) Число благоприятных исходов вынуть синий карандаш m=5 P(A)=5/8 б) Число благоприятных исходов вынуть красный карандаш m=3 P(A)=3/8 в) Число благоприятных исходов вынуть зеленый карандаш m=0 P(A)=0 г) Число благоприятных исходов вынуть синий или красный карандаш m=8 P(A)=0. 2. ( задачи 7.21 -7.30) В урне m = 4 белых шаров и n = 2 черных. Случайным образом вынимают 2 шара. Какова вероятность того, что шары: а) оба белые; б) оба черные; в) один белый, а второй – черный? Решение. Всего в урне m+n=4+2=6 шаров. Число способов достать 2 шара из 6 есть сочетание  . . а) Число способов достать 2белых шара из 4 белых шаров есть сочетание 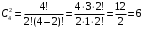 Вероятность вынуть два белых шара Р(А) = 6/15 = 2/5 б) Число способов достать 2черных шара из 2 черных шаров есть сочетание 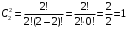 Вероятность вынуть два черных шара Р(В) = 1/15 в) Число способов достать 1 белый шара из 4 белых шаров и 1 черный из 2 черных шаров 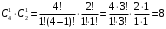 Вероятность вынуть один белый, а второй черный шар Р(С) = 8/15 Проверка: Р(А)+Р(В)+Р(С) = 6/15+1/15+8/15 = 1 3. (задачи 7.11 – 7.20) Найти надежность системы, состоящей из 5 независимых элементов с надежностями: . p1=p2=0.6, p3=0.5, p4=p5=0.7  Решение. Надежность независимых элементов 1, 2 и 3 определяем по закону сложения вероятностей совместных событий р1=3= р1+р2+р3-р1р2-р1р3-р2р3+р1р2р3=0.6+0.6+0.5-0.6·0.6-0.6·0.5-0.6·0.5+0.6·0.6·0.5=1.7-0.36-0.3-0.3+0.18=0.92 Надежность элементов 1-3 и 4 определяем по закону умножения вероятностей независимых событий р1-4=р1-3·р4=0.92·0.7=0.644 Надежность элементов 1-4 и 5 определяем по закону сложения вероятностей совместных событий: р1-5=р1-4+р5-р1-4·р5=0.644+0.7-0.644·0.7=1.344-0.4508=0.8932 Таким образом, надежность системы составляет р=0.8932 4. (задачи7.41 -7.50) Производительность первого конвейера в k раз больше, чем второго. Первый конвейер допускает p% брака, второй q% , брака. Детали с обоих конвейеров поступают на склад. а) Какова вероятность того, что случайно взятая со склада деталь будет стандартна? б) Какова вероятность того, что случайно взятая со склада деталь будет не стандартна? в) Случайно выбранная на складе деталь оказалась стандартной. Какова вероятность того, что деталь изготовлена на первом конвейере, на втором конвейере? k=4, p=10%, q=5%. Решение. Обозначим гипотезы: H1 – деталь с первого конвейера, H2 – деталь со второго конвейера. Вероятности гипотез: P(H1) = k/(k+1) =4/5=0.8, P(H2) = 1/(k+1) =1/5=0.2. Вероятность того , что деталь с первого конвейера стандартна Р(А/Н1) = 1-p =1-0.1 =0.9, со второго – P(A/H2) = 1-q = 1-0.05 =0.95. а) Событие А заключается в том, что со склада будет взята стандартная деталь. Вероятность Р(А) найдем по формуле полной вероятности: Р(А) = Р(А/Н1) P(H1) + Р(А/Н2) P(H2) = 0.9*0.8 + 0.95*0.2 = 0.91 б) Вероятность того, что взятая со склада деталь нестандартна (событие В, противоположное событию А) Р(В) = 1 – Р(А) = 1- 0.91 = 0.09. в) Для нахождения вероятности того, что взятая стандартная деталь изготовлена на первом контейнере , применим формулу Байеса: 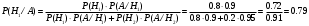 ? ?а на втором 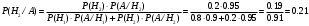 5. (задачи 7.51 -7.60) В первом ящике находится N деталей, из которых M – стандартны. Во втором ящике находится n деталей, из которых m стандартны. Без проверки на стандартность перекладывается из первого ящика во второй k деталей. Какова вероятность того, что случайно взятая из второго ящика деталь будет: а) стандартна; б) нестандартна? N =200, M = 90, n = 100, m = 85. Решение. а) Пусть событие А заключается в том, что случайно взятая деталь окажется стандартной. Рассмотрим следующие гипотезы: H1 – из первого ящика во второй перекладывают две стандартные детали. Вероятность этой гипотезы 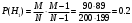 Во втором ящике теперь 102 детали( n+2), из которых 87 стандартные (m+2) Вероятность извлечь стандартную деталь из второго ящика в этой гипотезе 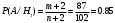 H2 - из первого ящика во второй перекладывают одну стандартную и одну нестандартную детали. Вероятность этой гипотезы 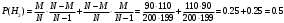 Вероятность извлечь стандартную деталь из второго ящика в этой гипотезе 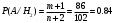 H3 – из первого ящика во второй перекладывают две нестандартные детали. Вероятность этой гипотезы 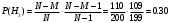 Вероятность извлечь стандартную деталь из второго ящика в этой гипотезе 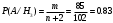 Вероятность того, что случайно взятая деталь из второго ящика окажется стандартной, найдем , используя формулу полной вероятности: 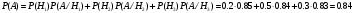 б) Вероятность того, что взятая из второго ящика деталь не стандартна ( событие В, противоположное событию А) Р(В) = 1 – З(А) = 1 – 0.84 = 0.16 6. Пример (задачи 7.61 -7.70 а)) На клумбу посеяно n семян цветов одного сорта со всхожестью P. Полагая, что μ – количество взошедших семян, найти вероятности событий: 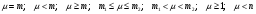 Р=60%; n=10; m=5; m1=3; m2=6. Решение. Для решения задачи воспользуемся формулой Бернулли и законом сложения вероятностей. а) Вероятность того, что количество взошедших семян 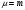 найдем по формуле Бернулли найдем по формуле Бернулли  По условию задачи p = 0.6, q= 1-p = 1-0.6 = 0.4 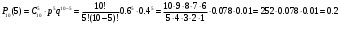 б) 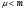 , то есть μ = 0, 1, 2, …m-1 = 0, 1, 2, 3, 4. Искомая вероятность равна , то есть μ = 0, 1, 2, …m-1 = 0, 1, 2, 3, 4. Искомая вероятность равна  Определим слагаемые вероятности   в)   г)  , то есть μ = 3, 4, 5, 6. Искомая вероятность равна , то есть μ = 3, 4, 5, 6. Искомая вероятность равна Определим вероятности   д)  Это событие, противоположное событию Это событие, противоположное событию  , то есть , то есть  е)  Это событие противоположное событию Это событие противоположное событию 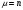 . Поэтому . Поэтому 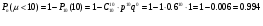 7. (задачи 7.61 – 7.70 б)) На клумбу посеяно n семян цветов одного сорта со всхожестью P. Полагая, что μ – количество взошедших семян, найти вероятности событий: 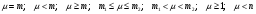 P = 0.9; n = 500; m = 203; m1 = 183; m2 = 220 Решение. При большом объеме данных вместо формулы Бернулли применяются теоремы Лапласса. а) 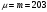 . Применим локальную теорему Лапласса: . Применим локальную теорему Лапласса: , ,Найдем 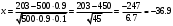 Функция 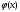 четная, поэтому по Таблице 2 найдем ее значение четная, поэтому по Таблице 2 найдем ее значение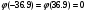 . Таким образом вероятность того, что из 500 семян взошло ровно 293 равна 0. . Таким образом вероятность того, что из 500 семян взошло ровно 293 равна 0.б)  Для нахождения вероятности того, что из 500 семян взойдет меньше 203 найдем, используя интегральную теорему Лапласса: Для нахождения вероятности того, что из 500 семян взойдет меньше 203 найдем, используя интегральную теорему Лапласса: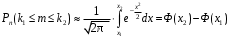 где  Найдем переменные фунуции Лапласса  Значения нечетной функции Лапласа 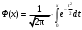 найдем по Таблице 3. найдем по Таблице 3.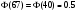 . Тогда искомая вероятность . Тогда искомая вероятность 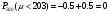 в) 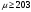 Это событие является противоположным предыдущему, поэтому Это событие является противоположным предыдущему, поэтому 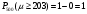 г) 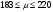 . Найдем переменные . Найдем переменные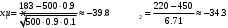  д)  . Поскольку переменные будут практически такими же, как и в предыдущем случае, вероятность события также будет равна 0 . Поскольку переменные будут практически такими же, как и в предыдущем случае, вероятность события также будет равна 0е) 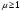 . Противоположное событие заключается в том, что не взойдет ни одно семя, то есть . Противоположное событие заключается в том, что не взойдет ни одно семя, то есть  . Используя локальную теорему Лапласса, найдем . Используя локальную теорему Лапласса, найдем 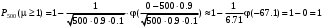 ж) 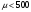 . Противоположное событие заключается в том, что взойдет ровно 500 семян, то есть . Противоположное событие заключается в том, что взойдет ровно 500 семян, то есть 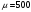 . Используя локальную теорему Лапласса, найдем . Используя локальную теорему Лапласса, найдем 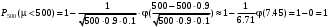 8 . (задачи 7.71-7.80) Дискретная случайная величина задана таблицей. Найти неизвестную вероятность p3 , математическое ожидание M(X), D(X) и вероятность попадания случайной величины в интервал α ≤X≤β 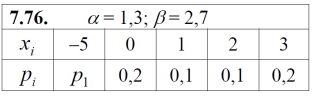 Решение. а) Найдем р1. Так как 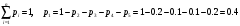 б) 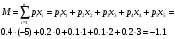 в) 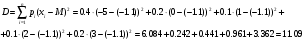 г) Построим функцию распределения случайной величины:  Рассмотрим различные значения х. 1) Если х<-5, то 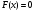 2) Если 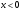 , то , то 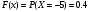 3) Если 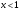 , то , то  4) Если  , то , то 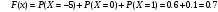 5) Если 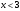 , то , то 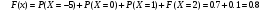 6) Если 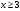 , то , то 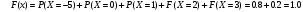 Функция распределения имеет вид:  Искомая вероятность 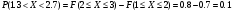 9. (задачи 7.81-7.90) Дискретная случайная величина задана таблицей. Найти неизвестное значение xi , неизвестную вероятность Pi , дисперсию D(X), среднеквадратичное отклонение σ( x) и вероятность событий Х < M(Х) и Х ≥ M(Х) M(x) = 0.45
. Решение. а) Найдем р2. Так как  б) Неизвестную величину x3 найдем по известному значению М(х) 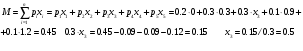 в) Определим дисперсию случайной величины 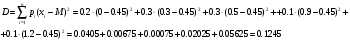 г) Среднеквадратичное отклонение случайной величины г) Среднеквадратичное отклонение случайной величины 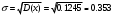 д) Для нахождения вероятности Р(Х < M(Х)) построим функцию распределения случайной величины. 1) Если х<0, то 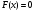 2) Если 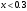 , то , то 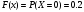 3) Если 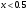 , то , то 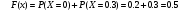 4) Если 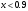 , то , то 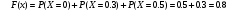 5) Если 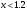 , то , то 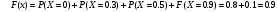 6) Если 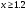 , то , то 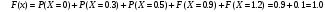 Функция распределения имеет вид:  Искомая вероятность 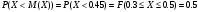 е) Вероятность P(X≥M(X)) =1 – P(X<M(X)) = 1- 0.5 = 0.5 10. (задачи 7.91-7.100) Дана функция распределения F(x) случайной величины X . Найти плотность распределения вероятности f(x) , математическое ожидание M(X) и вероятность попадания случайной величины в интервал х1≤Х x1= 0.1 x2 =3  Решение. а) По определению 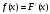 . Поэтому . Поэтому б) По определению математическое ожидание непрерывной случайной величины 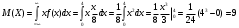 в) Вероятность попадания случайной величины в интервал (х1,х2) 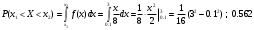 11. (задачи 7.131-7.140) Непрерывная случайная величина распределена по нормальному закону с параметрами а и σ . Найти вероятности событий Х < А; X > B; А ≤ X ≤ B; |X – a| < t σ . Найти интервал [а – σ , а + σ ] , в который случайная величина попадает с вероятностью Р a = 2; σ = 5; A = 4; B = 10; t = 1.5; P = 0.8 Решение. а) Вероятность попадания случайной нормально распределенной величины в заданный интервал определяется по формуле 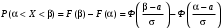 Используя Таблицу 2 значений функции Лапласса, с учетом ее нечетности, получим  б) 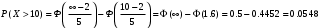 в) 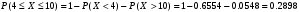 г) Используя Табицу 2 найдем вероятность 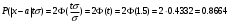 д) Найдем интервал [а – σ , а + σ ], в который случайная величина попадает с вероятностью Р=0.8. Воспользуемся формулой 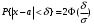 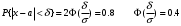 По Таблице 2 находим 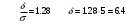 |
