Эконометрика. Практических заданий по дисциплине эконометрика
 Скачать 47.22 Kb. Скачать 47.22 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ ЭКОНОМЕТРИКА Группа Го19Э271 Студент Н.Л.Батуро МОСКВА 2021 Укажите основные этапы эконометрического исследования. Обычно выделяют шесть основных этапов эконометрического моделирования: постановочный, априорный, этап параметризации, информационный, этапы идентификации и верификации модели. I этап (постановочный). Формируется цель исследования, определяется набор участвующих в модели экономических переменных. При выборе экономических переменных необходимо теоретическое обоснование каждой переменной (при этом рекомендуется, чтобы число их было не очень большим и, как минимум, в несколько раз меньше числа наблюдений). Объясняющие переменные не должны быть связаны функциональной или тесной корреляционной зависимостью, так как это может привести к невозможности оценки параметров модели или к получению неустойчивых, не имеющим реального смысла оценок, т. е. к явлению мультиколлинеарности. II этап (априорный). Проводится анализ сущности изучаемого объекта, формирование и формализация априорной (известной до начала моделирования) информации. III этап (параметризация). Осуществляется непосредственно моделирование, т.е. выбор общего вида модели, выявление входящих в нее связей. Основная задача, решаемая на этом этапе, — выбор вида функции f(X) в эконометрической модели (1.1), в частности, возможность использования линейной модели как наиболее простой и надежной. От того, насколько удачно решена проблема спецификации модели, в значительной степени зависит успех всего эконометрического моделирования. IV этап (информационный). Осуществляется сбор необходимой статистической информации — наблюдаемых значений экономических переменных. Здесь могут быть наблюдения, полученные как с участием исследователя, так и без его участия (в условиях активного или пассивного эксперимента). V этап (идентификация модели). Осуществляется статистический анализ модели и оценка ее параметров. С проблемой идентификации модели не следует путать проблему ее идентифицируемости, т. е. проблему возможности получения однозначно определенных параметров модели, заданной системой одновременных уравнений (точнее, параметров структурной формы модели, раскрывающей механизм формирования значений эндогенных переменных, по параметрам приведенной формы модели, в которой эндогенные переменные непосредственно выражаются через предопределенные переменные). VI этап (верификация модели). Проводится проверка истинности, адекватности модели. Выясняется, насколько удачно решены проблемы спецификации, идентификации и идентифицируемости модели, какова точность расчетов по данной модели, в конечном счете, насколько соответствует построенная модель моделируемому реальному экономическому объекту или процессу. Следует заметить, что если имеются статистические данные, характеризующие моделируемый экономический объект в данный и предшествующие моменты времени, то для верификации модели, построенной для прогноза, достаточно сравнить реальные значения переменных в последующие моменты времени с соответствующими их значениями, полученными на основе рассматриваемой модели по данным предшествующих моментов. Назовите виды аналитических зависимостей, наиболее часто используются при построении моделей. 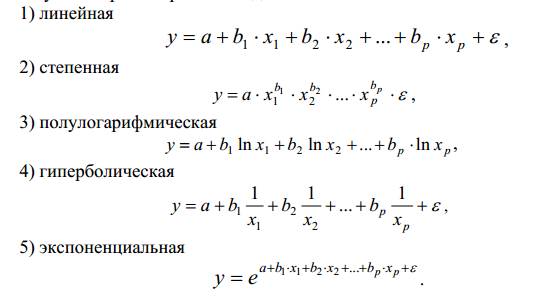 Охарактеризуйте функции, которые чаще всего используются для построения уравнения парной регрессии. Парной регрессией называется уравнение связи двух переменных у и х вида y = f (x), где у – зависимая переменная (результативный признак); х – независимая, объясняющая переменная (признак-фактор). Различают линейные и нелинейные регрессии. Линейная регрессия описывается уравнением: y = a + b ⋅ x + ε . Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам. Укажите, по какой формуле вычисляется выборочный коэффициент парной корреляции rxy . 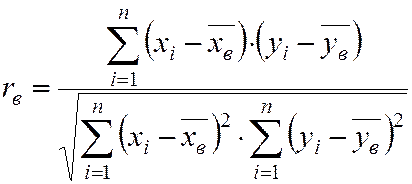 Объясните сущность метода анализа динамического ряда. При исследовании многих природных и производственных процессов возникает задача анализа в динамике событий и их последовательностей, которые не поддаются методам стандартного математического анализа, поскольку зависят от случайных факторов. Основными задачами в таких исследованиях являются детальное изучение этих процессов, выделение их существенных характеристик, которое может привести к возможности прогнозирования развития этих процессов в будущем. Также представляет интерес выделение внутренних закономерностей, которым подчинено развитие этих процессов. Временной ряд (динамический ряд, ряд динамики) – это последовательно измеренные через некоторые промежутки времени данные о значении какого-либо параметра исследуемого процесса (или нескольких параметров, в этом случае говорят о многомерном временном ряде). Временной ряд состоит из двух элементов: - периода времени, за который или по состоянию на который приводятся числовые значения; - числовых значений показателя, называемых уровнями ряда. Временные ряды бывают детерминированными (получены на основе значений некоторой неслучайной функции, например, ряд последовательных данных о количестве дней в месяцах) и случайными (результат реализации некоторой случайной величины). Классификация временных рядов проводится по следующим признакам. • По характеру показателя, для которого определяются уровни: - детерминированные ряды, которые получены на основе значений некоторой неслучайной функции, например, ряд последовательных данных о количестве дней в месяцах; - случайные ряды, представляющие собой реализацию некоторой случайной величины. • По форме представления уровней: - ряды абсолютных величин; - ряды относительных величин; - ряды средних величин. • По характеру временного показателя: - моментные ряды, в которых уровни характеризуют значение показателя по состоянию на определенные моменты времени; - интервальные ряды, уровни которых характеризуют значение показателя за определенные периоды времени. Важная особенность интервальных временных рядов абсолютных величин заключается в возможности суммирования их уровней. • По расстоянию между датами и интервалами времени: - полные или равноотстоящие ряды, если даты регистрации или окончания периодов следуют друг за другом с равными интервалами; - неполные или неравноотстоящие ряды, если принцип равных интервалов не соблюдается или имеются пропущенные значения. При изучении рядов динамики обычно решают следующие задачи: 1. Вычислить числовые и функциональные характеристики ряда (описательные методы). 2. Определить, имеется ли некоторая неслучайная, закономерная компонента, описывающая тенденцию (тренд) процесса. 3. Определить, нет ли регулярных, колебательных “сезонных” компонент, которые связаны с периодическими естественными колебаниями параметров случайного процесса. 4. Выделить и описать основные колебания случайного процесса вокруг тренда, в случае необходимости удалить влияние второстепенных факторов. 5. Дать прогноз развития случайной процесса на ближайшее будущее и указать степень уверенности в этом прогнозе. Следует иметь в виду, что при изучении рядов динамики необходимо соблюдение ряда условий: • Статистические данные должны быть сопоставимы по территории, кругу охватываемых объектов, единицам измерения, времени регистрации, ценам, методологии расчета. Сопоставимость по территории означает, что данные по странам и регионам, границы которых изменились, должны быть пересчитаны в старых пределах. Сопоставимость по кругу охватываемых объектов означает сравнение совокупностей с равным числом элементов. Сопоставимость обеспечивается так называемым смыканием рядов динамики. При этом абсолютные уровни могут заменяться относительными, иногда делают пересчет в условные абсолютные уровни и т. п. • Числовые уровни рядов динамики должны быть упорядоченными во времени. Не допускается анализ рядов с пропусками отдельных уровней (неполных динамических рядов), если же такие пропуски неизбежны, то их восполняют условными расчетными значениями. • Временные ряды применяются только для краткосрочного прогнозирования (чаще всего на 1 период вперед). • Для анализа и прогноза необходима достоверная информация о развитии исследуемого явления минимум за пять периодов. Задачи: Рассчитать коэффициенты для различных видов зависимостей. Исходные данные в табл.3 Таблица 3. Регрессионный анализ.
Вариант №1
Вычислить коэффициент корреляции для линейной зависимости. Исходные данные в таблице 4. Таблица 4. Корреляционный анализ.
Вариант №1 Коэффициент корреляции (r) равен = (19670.6-150*(450.02/5))/(√((5500-150*150/5)*(87362.8642-450.02*450.02/5))) = 0.9013 Полученное значение коэффициента корреляции говорит о наличии прямой связи между X и Y. Величина коэффициента корреляции показывает, что связь между X и Y сильная (очень тесная). |
