ПЗ МАТ. АНАЛИЗ 1-1. Практических заданий по дисциплине математический анализ
 Скачать 41.91 Kb. Скачать 41.91 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ МАТЕМАТИЧЕСКИЙ АНАЛИЗ Группа Мс20Э111 Студент А.В. Лис МОСКВА 2021 Задача 1. Вычислить пределы последовательностей  Решение Вычисляем пределы числителя и знаменателя отдельно  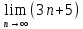 Вычисляем предел     Поскольку выражение  является неопределенностью, попробуем преобразовать выражение является неопределенностью, попробуем преобразовать выражение Выносим за скобки общий множитель n    Сокращаем дробь на n  Вычисляем предел 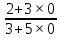 Упрощаем выражение  Ответ   . Решение Вычисляем предел каждого слагаемого отдельно   Вычисляем предел 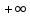 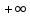 Поскольку выражение 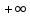  является неопределенностью, попробуем преобразовать выражение является неопределенностью, попробуем преобразовать выражение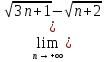 Умножаем выражение на  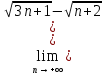 Вычисляем произведение 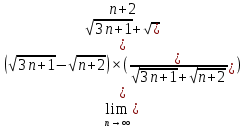 Используя 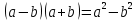 , упрощаем произведение , упрощаем произведение Когда перед скобками стоит знак 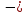 , изменяем знак каждого члена в скобках , изменяем знак каждого члена в скобках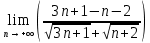 Приводим подобные члены  Вычисляем разность  Выносим за скобки общий множитель     Сократим дробь на   Вычисляем пределы числителя и знаменателя отдельно   Вычисляем предел 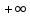  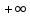 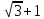 Поскольку выражение  , , 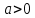 определено как определено как 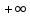 , предел , предел Равен 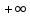 Ответ  Задача 2. Найти производные сложных функций 2.1.  2.1. Решение Возьмем производную от обеих частей 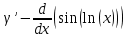 Используя правило дифференцирования сложной функций,  , где , где  вычисляем производную вычисляем производную Находим производную 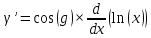  Делаем обратную замену   Вычисляем произведение  Ответ  2.2.  2.2. Решение Возьмем производную от обеих частей 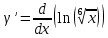 Используя  , преобразовываем выражение , преобразовываем выражение Используя 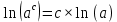 , преобразовываем выражение , преобразовываем выражение Используя правило дифференцирования 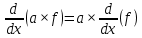 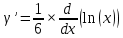 Используя правило 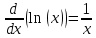 , вычисляем производную , вычисляем производную Умножаем дроби  Ответ  Задача 3. Вычислить неопределенный интеграл 3.1.  3.1. Решение Преобразовываем интеграл используя подстановку 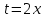  Используя свойство интегралов   Вычисляем интеграл методом интегрирования по частям  Используя свойство интегралов  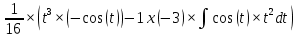 Любое выражение, умноженное на 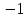 , равно ему противоположному , равно ему противоположному Используем переместительный закон, чтобы изменить порядок членов  Вычисляем интеграл методом интегрирования по частям 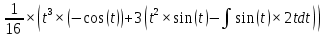 Используя свойство интегралов   Используем переместительный закон, чтобы изменить порядок членов 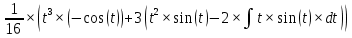 Вычисляем интеграл методом интегрирования по частям  Используем свойство интегралов 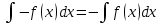  Используя 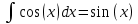 , находим интеграл , находим интеграл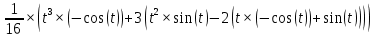 Делаем обратную замену 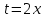  Упрощаем выражение 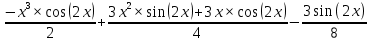 Прибавляем константу интегрирования  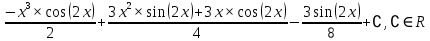 Ответ 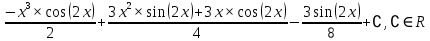 3.2.  3.2. Решение Для подготовки к интегрированию по частям, определяем u и dv 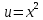  Вычисляем дифференциал по формуле  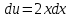  Определяем 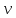 путем вычисления интеграла путем вычисления интеграла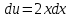  Подставляем 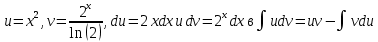  Используем свойство интегралов   Вычисляем произведение 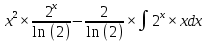 Используем переместительный закон, чтобы изменить порядок членов  Вычисляем интеграл методом интегрирования по частям 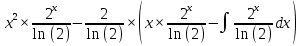 Используем свойство интегралов   Используя  находим интеграл находим интеграл Упрощаем Выражение 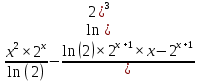 Прибавляем константу интегрирования  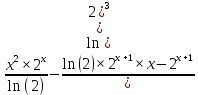 Ответ 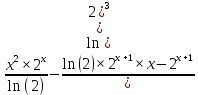 Задача 4. Найти частные производные первого и второго порядка 4.1.  4.1. Решение При нахождении 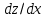 считаем аргумент постоянным считаем аргумент постоянным При нахождении  считаем аргумент считаем аргумент 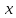 постоянным постоянным Находим вторые частные производные 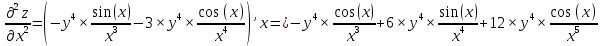  Ответ  ; ;  ; ;  ; ;  . .4.2. 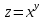 4.2. Решение При нахождении 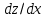 считаем аргумент считаем аргумент  постоянным постоянным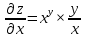 При нахождении  считаем аргумент считаем аргумент 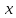 постоянным постоянным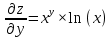 Находим вторые частные производные   Ответ 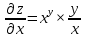 ; ; 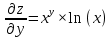 ; ; 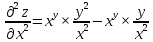 ; ;  |
