ббб. Практикум по экологии Автор Преподаватель гбоу спо сергиевский губернский техникум

• Название: Практикум по экологии Автор Преподаватель гбоу спо сергиевский губернский техникум
• Дата: 07.10.2021
• Размер: 1.92 Mb.
• Имя файла: 19307110741.doc
• Тип: Практикум; #243301
• страница: 11 из 14

Нормированное отклонение

Нормированное отклонение – это показатель, характеризующий отдельную варианту или группу вариант. Обозначается буквой Н.

Нормированное отклонение – это величина, которая указывает, на сколько долей среднего квадратического отклонения каждый конкретный член совокупности отклоняется от средней арифметической. Вычисляется он по формуле:

г
де Н – нормированное отклонение;

Х_ср – средняя арифметическая;

S – среднее квадратическое отклонение.

Как и коэффициент изменчивости, нормированное отклонение – величина относительная. Каждая варианта характеризуется определенным значением Н. Если Н какой-либо варианты равно +1, значит эта варианта больше Х на 1. Чем больше значение Н, тем дальше от средней арифметической отстоит данная особь.

Ошибка статистических величин

Для изучения изменчивости того или иного признака берут не всех представителей, а только часть их (выборочную совокупность или выборку). В каждом конкретном случае в выборку могут попасть особи, имеющие несколько более высокие или более низкие значения признака, поэтому вычисленные значения биометрических величин будут отражать свойства генеральной совокупности с определенными ошибками. Эти ошибки не могут быть устранены при самой тщательной организации исследований, но их можно учесть. Они получили название ошибок репрезентативности или выборочности.
Ошибки статистических показателей будут тем больше, чем выше изменчивость признака и чем меньше объем выборки.

Ошибки статистических показателей обозначаются буквой m. Чтобы различать, к какому показателю относится ошибка, рядом с условным ее обознчением подстрочно приписывается обозначение данного показателя.

Например. m_x – ошибка средней арифметической,

m_S – ошибка среднего квадратического отклонения,

m_{cv –} ошибка коэффициента изменчивости.


Все ошибки измеряются в тех же единицах, что и сами показатели. Ошибки статистических показателей вычисляются по формулам:

где m_x – ошибка средней арифметической,

S – среднее квадратическое отклонение,

n – объем выборки





где m_S – ошибка среднего квадратического отклонения,

S – среднее квадратическое отклонение,

n
– объем выборки.

где m_cv – ошибка коэффициента изменчивости,

С_cv – коэффициент измечивости,

n – объем выборки.

Ошибки статистических показателей позволяют уточнить границы, в которых находится фактическое значение данных показателей. Такими границами считается интервал, равный промежутку: показатель 2 ошибки.

В нашем примере





2m_x =  1,3 X = 53,5  1,3 кг.

Вычислить m_ср , m_S, m_cv для изучаемых Вами признаков.

Критерий достоверности

и достоверность разности между средними

Критерий достоверности позволяет определить, насколько велика допущенная в опыте ошибка. Его обозначают буквой t и вычисляют по формуле:
Если критерий достоверности больше 3 (t3), то данные опыта достоверны, ошибка составляет около 5%. Если критерий достоверности меньше 3 (t3),то полученным данным верить нельзя.


Критерий достоверности зависит от размаха изменчивости и от числа наблюдений. Если t3, то нужно увеличить выборку, взять для наблюдений больше особей, проверить, нет ли случайных значений вариант. В нашем примере

Полученное число больше 3, значит данные достоверны.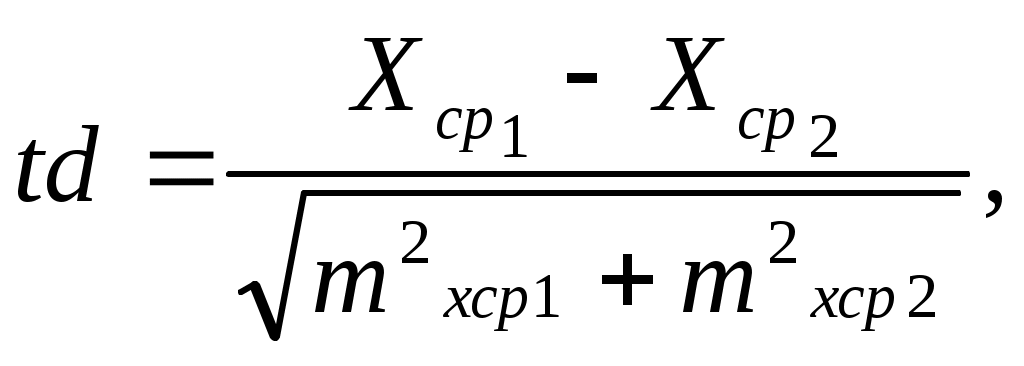


При сопоставлении данных двух изучаемых групп можно вычислить достоверность разницы данного показателя между ними. Для этого вычисляют критерий достоверности различий. Этот показатель предложил В.С.Госсет, публиковавший свои работы под псевдонимом Стьюдент, отсюда и название – критерий Стьюдента. Критерий Стьюдента td вычисляют по формуле:

где td– показатель достоверности разности,

X
_ср1 – X _{ср2 –} разность между средними арифметическими двух сравниваемых групп (от большего значения Х_ср вычисляется меньшее),

Разность притнято считать достоверной, если td факт td табл.

Табличное значение td (t) выбирается по таблице, которая помещается в каждом учебнике по биометрии. Под числом степеней свободы Y (ню) понимается число наблюдений, уменьшенное на число ограничений.

Например: n₁= 50, n₂= 50, Y = (n₁ – 1) + ( n₂ – 1) = (50–1) + (50 – 1) = 98.

В таблице даются достоверные величины td при трех порогах вероятности (Р): 0,95; 0,99; 0,999 с учетом числа степеней свободы. Оптимально будет выбрать уровень Р 0,95. В месте пересечения строки значения Y и графы уровня вероятности и находится табличное значение td. Так, при значении Y=99 и Р 0,95 td табличное равно 1,98.

Если td_факт. td_табл., то разность принято считать недостоверной, т.к. при этом нельзя сказать, какая из двух сравниваемых генеральных средних имеет лучшие показатели и сохранится ли подобная зависимость в других исследованиях или опытах.

Например, сравнивая по весу 2 группы детей, имеем:

Х₁ = 23 кг (23,0) m_хср1 = 3,1 кг,

Х₂ = 24 кг (24,0) m_хср2 = 2,0 кг,

Т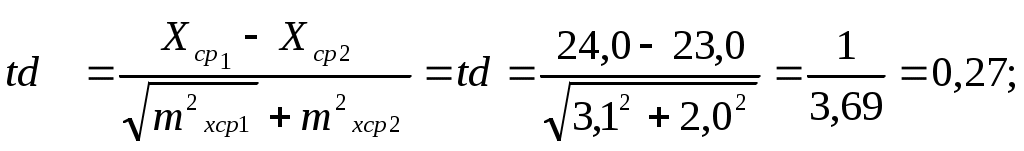
аким образом, td_факт = 0,27 td_табл. Значит, вес детей в 2-х группах различается недостоверно, т.е. нельзя сказать, какая группа имеет лучшие показатели.