учебная логика. учебник СПО. Практикум по программному обеспечению содержит большое количество примеров и заданий
 Скачать 5.66 Mb. Скачать 5.66 Mb.
|
Задание 3.5.14Постройте график функции f(x)=1/x , где x [-5;5] шаг 0,5.∈ Обратите внимание на поведение графика в точке x=0. Для исправления ситуации удалите значение функции в точке x=0. Задание 3.5.15Постройте семейство косинусоид вида y=a cos‧ (b ‧ x )+c на отрезке [0;4] с шагом табуляции 0,2. Значения констант a, b, c занесены в отдельные ячейки. На листе 3. Начиная с ячейки А6 создайте таблицу значений коэффициентов.
А ниже, начиная с ячейки А11 и до А14, создайте таблицу значений функции при разных коэффициентах (значения располагаются по строкам).
В ячейку B11 введите 0, в ячейку С11 введите 0,2. С помощью маркера заполнения заполните 11-ую строку таблицы вправо. В ячейку B12 введите формулу косинусоиды, используя коэффициенты a, b, с из строки 7. Относительными или абсолютными должны быть адреса? Скопируйте формулу вправо. Аналогично введите формулы в B13 и B14, используя последующие значения из таблицы коэффициентов. Выделите полученную таблицу. Постройте диаграмму. Используйте тип «Точечная». Измените некоторые значения коэффициентов в таблице коэффициентов. Как меняются графики функций? Задание 3.5.16Постройте параметрическую функцию: x=2cos3t y=2sin3t где t [0 ; 6], шаг табуляции 0,2. ∈ Отведем для таблицы строки с 40 по 42. В ячейках А40-А42 запишите:
С помощью автозаполнения заполните строку 40 значениями от 0 до 6 с шагом 0,2. В ячейку В41 введите формулу для вычисления значений х. Скопируйте вправо. Введите формулу для вычислений значений у в ячейку В42. Скопируйте вправо. Выделите 41 и 42 строки таблицы и постройте точечную диаграмму. Задание 3.5.17Построение поверхности гиперболического параболоида z = x2-y2 x ∈ [-3;3], y [-3,3], шаг табуляции 0,5.∈ С помощью автозаполнения введите значения х. Заполните столбец А (например строки от 71 до 83) значениями от -3 до 3 с шагом 0,5. Аналогично введите значения у (ячейки В70: N70). В ячейку В71 введите формулу для вычисления значений z. Подумайте, как использовать здесь абсолютную и относительную адресацию. Вспомните пример с таблицей умножения. Заполните формулу вправо и вниз на все ячейки таблицы. Выделите блок В71:N83. Постройте диаграмму, тип – линии. 3.5.8. Поиск оптимального решенияЕсть целый класс задач, связанных с поиском оптимального решения. Рассмотрим одну из них. Некоторое предприятие производит продукцию двух видов П1 и П2 из сырья трех видов С1, С2 и С3. Запасы сырья на складе С1 – 200 единиц, С2 – 400 единиц и С3 – 300 единиц. Для производства продукции П1 требуется 2 единицы сырья С1, 8 единиц сырья С2, 5 единиц сырья С3. Для производства продукции П2 требуется 5 единиц сырья С1, 5 единиц сырья С2, 6 единиц сырья С3. Завод не может выпускать более 100 единиц каждой продукции в день. Доход от продажи единицы продукции П1 – 50 у.е., П2 – 40 у.е. Сколько единиц каждой продукции надо произвести, чтобы прибыль была максимальна? Для решения подобных задач можно использовать Решатель, который запускается Сервис – Поиск решения (если этого пункта меню нет, то необходимо установить расширение Solver). Составьте следующую таблицу (рис. 3.17). 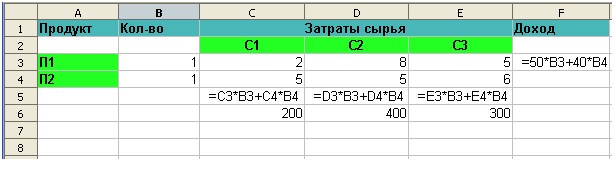 Рис. 3.17. Составление таблицы для поиска оптимального решения В ячейках В3 и В4 указано произвольное количество вырабатываемой продукции, ячейки C5, D5, E5 содержат формулы для расчета затрат сырья каждого вида, ячейки C6, D6, E6 – запасы сырья на складе, в ячейке F3 вычисляется доход от производства продукции. Выделите ячейку F3. В пункте меню Сервис найдите «Поиск решения» (или Solver). В зависимости от того, какое расширение установлено, откроется окно «Решатель» или окно «Оптимальное решение». В открывшемся окне «Решатель»: Установить целевую ячейку $F$3; o Результат – максимальное значение; o Изменяя ячейки – В3:В4 o Добавить ограничения: Ссылка на ячейку: С5 Условие: < = Ограничение: С6 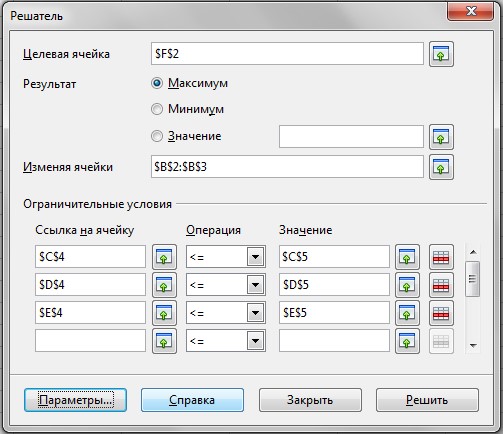 Рис. 3.18. Решатель Аналогично для D5, D6 и E5, E6. Далее следует установить еще некоторые огра- ничения, открыв окно «Параметры»: переменные принять как неотрицательные и целочисленные. После указания всех ограничений нажать кнопку «Решить». Автоматически должно быть найдено решение: П1 = 40, П2 = 16. Решение необходимо сохранить. |
