учебная логика. учебник СПО. Практикум по программному обеспечению содержит большое количество примеров и заданий

• Название: Практикум по программному обеспечению содержит большое количество примеров и заданий
• Анкор: учебная логика
• Дата: 12.09.2022
• Размер: 5.66 Mb.
• Имя файла: учебник СПО.docx
• Тип: Практикум; #672419
• страница: 41 из 50

Задание 3.7.8

Выполните тоновую коррекцию этой же фотографии с использованием команды Цвет – Авто. Сравните результаты, полученные при помощи автоматической коррекции и с использованием команды Яркость – Контраст.

Эта команда выполняет перераспределение яркостей пикселей автоматически. Анализируя изображение, GIMP находит самый светлый и самый темный пиксели и определяет их как белый и черный, а все остальные тона распределяет между ними.

Иногда результаты выполнения этой команды бывают неудовлетворительными.

Задание 3.7.9

Выполните тоновую коррекцию изображения с использованием команды Кривые.

Настройка кривых позволяет настраивать цвета более тонко.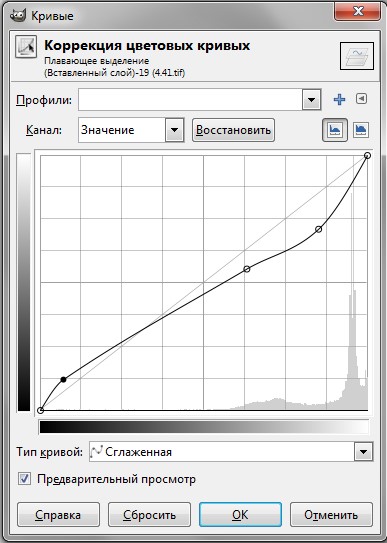



Рис. 3.43. Коррекция цветовых кривых

Когда вы открываете диалоговое окно «Кривые», самой кривой вы не увидите. Вместо этого вы увидите сетку, на которой расположена прямая линия, направленная по диагонали. Горизонтальная ось этого графика соответствует исходным значениям (входным уровням) изображения или выделенной области, а вертикальная ось соответствует новым значениям (выходящим уровням). При первом открытии этого диалогового окна график отображается в виде прямой, так как значения еще не изменялись. Все пиксели имеют одинаковые входящие и выходящие значения.

Можно поставить на кривой несколько контрольных точек и с их помощью отрегулировать вид кривой и, следовательно, яркость изображения. На изображении выбирайте точки, цвета которых необходимо откорректировать. В результате вы увидите эти точки на графике. Перетягивайте точки, соответствующие темным тонам, вверх, а точки, соответствующие светлым тонам, – вниз. Чтобы удалить точку, которую вы поставили, перетяните ее за пределы графика.

3.7.9. Рисование

В GIMP к инструментам рисования относятся:

«Кисть», «Карандаш», «Аэрограф», «Ластик», «Заливка», «Градиент», «Штампы», «Палец», «Осветление и Размывание».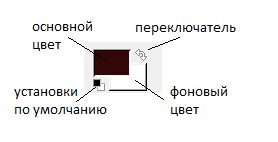



Рис. 3.44. Панель выбора цвета

Цвет переднего плана (или основной) используется для рисования, заливки выделенных областей, а также в качестве начального цвета градиента.

Цвет заднего плана (или фоновый) можно сравнить с цветом холста, на который наносится краска. Именно этот цвет появляется при удалении пикселей изображения (после удаления краски виден холст). Кроме того, фоновый цвет используется для завершения градиента.

По умолчанию основной цвет – черный, а фоновый – белый (рис. 3.44). Цвета переднего и заднего плана указываются в цветовых полях на панели инструментов. Используя «Переключатель цветов», основной и фоновый цвета можно менять местами. Щелчок на пиктограмме «Основной и фоновый цвета по умолчанию» восстанавливает черный цвет в качестве основного, а белый – в качестве фонового.

Щелчок по пиктограмме «Фоновый цвет» или «Основной цвет» откроет окно «Палитра цветов», с помощью которой устанавливается нужный цвет.

Кончик инструментов рисования имеет определенный размер и форму – размер кисти и форму кисти. Кроме того, каждый инструмент имеет параметры, которые определяют характер их работы. Форма инструмента отображается во вкладке «Кисти» вспомогательной панели, а параметры – в панели «Параметры инструмента», настройка «Масштаб» определяет размер кончика инструмента рисования.

Задание 3.7.10

Установите размер и параметры карандаша и создайте простой рисунок.

В панели «Параметры карандаша» обратите внимание, что исходная степень непрозрачности карандаша равна 100%. Откройте вкладку «Кисти» вспомогательной панели, где установите форму кончика карандаша и ее размер.

Если вам не нравится то, что получается, можно ластиком стереть неудачные штрихи.

Чтобы закрасить фрагменты рисунка, воспользуйтесь инструментом «Заливка».

Выберите цвет заливки (основной цвет) и закрасьте замкнутую область.

3.8. Системы компьютерной математики

(математические пакеты)

Еще недавно для решения математических задач пользователь должен был не только разбираться в математике, но и освоить язык программирования (и не один), знать сложные численные методы. Сейчас разработаны математические пакеты, которые позволяют решать различные математические задачи.

Ранние математические пакеты были ориентированы только на численные расчеты, для чего использовались возможности развитых численных методов. Но применение численных методов имеет ряд недостатков. Это, прежде всего, нахождение только частных решений и некоторая погрешность вычислений.

Высочайшим достижением стали системы компьютерной математики, выполняющие аналитические (символьные) преобразования. Еще недавно это было фантастикой. Аналитические методы решения задач дают общие (формульные) результаты и без погрешностей. Поэтому сейчас системы аналитических вычислений – наиболее интересное и развивающееся направление компьютерной математики.

Современные системы компьютерной математики обеспечивают и численные и символьные вычисления.

Спектр задач, решаемых подобными системами, очень широк:

• 
  проведение математических исследований, требующих вычислений и аналитических выкладок;
  
• 
  разработка и анализ алгоритмов;
  
• 
  математическое моделирование и компьютерный эксперимент;
  
• 
  анализ и обработка данных;
  
• 
  визуализация, научная и инженерная графика;
  
• 
  разработка графических и расчетных приложений.
  

3.8.1. Команды главного меню

Обычно главное меню систем компьютерной математики включает следующие команды.

Author – ввод пользователем исходной задачи.

Build – построение математических выражений из имеющихся фрагментов.

Calculus – вычисление.

Declare – объявление переменных, векторов, матриц и функций.

Expand – раскрытие выражения, перемножение его членов, упорядочение по степеням.

Factor – разложение на простые множителя чисел и выражений.

Solve – решение уравнений.

Simplify – упрощение выражений.

Approx – приближенное вычисление выражений.

3.8.2. Особенности работы

с математическими пакетами

Современный уровень развития компьютерной алгебры не исключает отказа от выполнения символьных вычислений (система возвращает исходное выражение). Многие преобразования имеют ограниченную область применения. Поскольку при упрощении выражений система, должна выполнять только корректные преобразования, компьютеру может потребоваться квалифицированная помощь: подсказать направление дальнейших преобразовании, сузить класс значений параметра. Поэтому во многих системах имеются средства указания областей определения переменных.

Результаты некоторых преобразований выглядят неожиданными. Такие сюрпризы могут быть связаны с неоднозначностью функций, их взаимозаменяемостью и главным образом – с вынужденной стандартизацией методов решения. Именно поэтому системы компьютерной математики не могут справиться с отдельными задачами, решения которых вошли в широко известные справочники. Это объяснимо: красивые нестандартные решения копились сотни лет и иногда достигались весьма искусственными приемами. Поэтому, например, при сравнении результата интегрирования с табличным следует иметь в виду возможность эквивалентных преобразований и различного представления констант. В таких случаях нужно получить разность интегралов, упростить ее и убедиться в том, что эта разность не зависит от переменной интегрирования.

Результатом символьного решения дифференциальных уравнений в общем случае является уравнение, связывающее зависимую и независимую переменные. Полезно выполнить его дифференцирование и затем контрольную подстановку.

При решении нелинейных уравнений и систем уравнений обычно требуется указание начальных приближений или области нахождения корней. В первом случае, как правило, находится единственное решение, в «области притяжения» которого оказалось исходное приближение, и для получения нового решения требуется сменить исходную точку. Если возможны комплексные корни, то, по крайней мере, одно приближение должно быть комплексным. Во втором за одно обращение возможно получение нескольких решений, но можно остаться ни с чем, поскольку процесс при выходе из указанной области завершается аварийно. «Свободный» поиск не имеет этих недостатков, но идет дольше и может завершиться отказом по исчерпанию предельного числа шагов. Во многих пакетах имеется возможность применить для решения системы несколько процедур, различающихся способами подготовки исходных данных.

В математических пакетах, конечно же, есть ошибки как на концептуальном уровне, так и на уровне программной реализации. Поэтому необходимо критически относится к полученным результатам и осуществлять проверку. Такие возможности может дать только знание математики.

3.8.3. Наиболее распространенные системы

компьютерной математики

Самыми богатыми возможностями обладают профессиональные пакеты Mathematica и Maple. Они же предъявляют самые высокие требования к аппаратуре и наиболее сложны в освоении.