учебная логика. учебник СПО. Практикум по программному обеспечению содержит большое количество примеров и заданий

• Название: Практикум по программному обеспечению содержит большое количество примеров и заданий
• Анкор: учебная логика
• Дата: 12.09.2022
• Размер: 5.66 Mb.
• Имя файла: учебник СПО.docx
• Тип: Практикум; #672419
• страница: 45 из 50

Задание 3.9.2

1. 
   Разложите на множители –1-х²+х³+х^5.
   
2. 
   Раскройте скобки в выражении (1+х)(2+2х+3х²) (х³+4х+3), проверьте правильность ответа с помощью обратной функции.
   

3.9.5. Решение уравнений

Для решения уравнений служит пункт меню «Уравнения».

Например, решим уравнение 2*x^3-3*x^2+6*x+4=0.

Для этого

− зададим в строке ввода левую часть уравнения: 2*x^3-

3*x^2+6*x+4;

− выбираем в меню: Уравнение – Решить, проверяем правильность выражения и задаем переменную, по которой решаем уравнение;

− нажать «ОК».

Для решения уравнений может использоваться функция: solve ([аргументы], [переменные]).

Аргументами являются левая часть уравнения или система уравнений, записанных через запятую, далее – переменная, относительно которой решается уравнение или список переменных.

Например, solve([2*x^3-3*x^2+6*x+4],[x]) Задание 3.9.3 Решите уравнение:

Решение систем уравнений

Для решения систем используется пункт меню: Уравнения – Решить линейную систему... или Уравнения – Решить алгебраическую систему...

− задается количество уравнений в системе;

− задаются левые части уравнений и список переменных;

− нажмите «ОК».

Для решения системы уравнений может быть использована функция Solve, при этом уравнения системы записываются в квадратных скобках через запятую, список аргументов – в квадратных скобках через запятую.

Например, solve([x^3-3*y^2, x+y-2],[x,y]).

Задание 3.9.4

Решите следующие системы уравнений:

1)

2)

3.9.6. Вычисление сумм

Для вычисления суммы ряда используется функция sum, которая может быть вызвана командой меню Анализ – Вычислить сумму и заполнить форму (рис. 3.46).



Рис. 3.46. Окно вычисления суммы

В ычисление суммы : sum(f(i), i, a, b);

Задание 3.9.5

Вычислите следующие суммы:

1. 
   ;
   
2. 
   .
   

3.9.7. Вычисление пределов и дифференцирование

Для нахождения пределов нужно выбрать пункт меню Анализ – Найти предел и заполнить следующую форму

(см. рис. 3.47).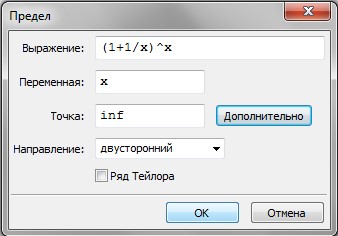



Рис. 3.47. Окно вычисления пределов

Или использовать функцию: limit(выражение, переменная, предел) Например, limit((1+1/x)^x, x, inf);

Для нахождения производной надо выбрать пункт меню Анализ – Дифференцировать. В окне «Дифференцировать» задается выражение, переменная, по которой надо искать производную и множитель – порядок производной (рис. 3.48).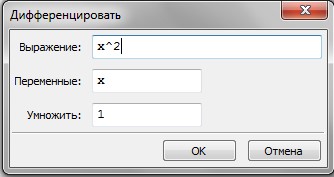



Рис. 3.48. Окно дифференцирования

Можно использовать функцию diff, например, diff(x^2, x).

Если нужно найти производную более высокого порядка, то в поле «Умножить» введите порядок производной.

Задание 6

Вычислите пределы:

1. 
   п ри х→1;
   
2. 
   при х→0;
   
3. 
   при х→3 справа и слева и при х→∞;
   
4. 
   В ычислите производные функции с 1 по 5 порядок двумя способами (последовательно и сразу).
   

3.9.8. Интегралы

Для нахождения интегралов используется пункт меню Анализ – Интегрировать.

Задание 7

Вычислите интегралы:

1. 
   ;
   
2. 
   ;
   
3. 
   ;
   
4. 
   .
   

3.9.9. Графики функций

1. 
   Построим график функции y=x² на отрезке [-4;4].
   

Пункт меню: Графики – График 2D. Откроется окно параметров графика (рис. 3.49).



Рис. 3.49. Окно параметров графика 2D

− В поле «Выражение» задаем фунцию: x^2. − В поле переменная x из -4 к 4.

− Количество точек – 10 (как по умолчанию).

2. 
   Построим поверхность z=x²-y² на отрезке [-5;5] (рис. 3.50).
   

Пункт меню: Графики – График 3D.

− В поле «Выражение» задаем фунцию: x^2-y^2.

− В поле переменная x из -5 к 5.

− В поле переменная y из -5 к 5.

− Сетка 30*30 (как по умолчанию).



Рис. 3.50. Поверхность

Примечание. В поле выражение можно задавать несколько функций через запятую, чтобы построить несколько графиков на одном чертеже.

3. 
   Для построения графиков функций, заданных параметрически:
   
   • 
     В окне «График 2D» нажать кнопку «Дополнительно» и выбрать «Параметрический график».
     
   • 
     Задать параметрические уравнения функции, диапазон изменения аргумента.
     
   • 
     Нажать «ОК».
     

Для построения графика кривой, заданной параметрически используют параметр parameric. В общем случае команда выглядит так:

Plot2D([paramentric, x-выражение, у-выражение, [параметр, начало, конец], [nticks, количество]]), где x-выражение, у-выражение задают зависимость коор-

динат от параметра, nticks, количество – количество кусочков, на которые будет разбит интервал изменения параметра.

Пример. Построим параметрическую окружность

Plot2D([paramentric, cos(t), sin(t), [t, -%pi, %pi], [nticks,

300]])